
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Елементи кореляційного аналізу. Побудова вибіркових рівнянь регресії. Вибірковий коефіцієнт кореляції. Кореляційне відношенняСодержание книги
Поиск на нашем сайте
Залежність між двома випадковими величинами, за якої при зміні однієї з величин змінюється середнє значення другої, називається кореляційною залежністю. Кореляційну залежність між випадковими величинами Х і Y описують функції регресії (див. практ. заняття 8):
Якщо функції регресії лінійні, то кореляцію називають лінійною. Інакше кореляція називається нелінійною. До основних задач кореляційного аналізу відносяться з’ясування форми кореляційної залежності (вигляду функцій регресії) і оцінка сили кореляційної залежності між випадковими величинами. Перша із вказаних задач розв’язується шляхом побудови за вибірковими даними (xi, yi) (i = 1, 2, …, n) (12.1) емпіричної функції регресії, яку підбирають так, щоб вона якомога краще відображала характерні особливості статистичних даних. Практично ця задача збігається із задачею підбору емпіричних формул за експериментальними даними і найчастіше розв’язується методом найменших квадратів. Якщо точки Mi (xi, yi), побудовані за вибіркою (12.1) в системі координат XOY, групуються навколо прямої лінії, то підбирають лінійні функції регресії Коефіцієнти a 0, a 1, b 0, b 1 цих функцій, згідно з методом найменших квадратів, обчислюють за формулами
(для спрощення замість У випадку згрупованих даних відповідні формули мають вигляд
Лінійні рівняння регресії мають вигляд
Характеристикою силу зв’язку (тісноти лінійної залежності) між складовими Х та Y двовимірної випадкової величини (Х,Y) служить вибірковий коефіцієнт кореляції rв , який обчислюється за формулою
Чим ближче | rв | до одиниці, тим зв’язок сильніший; чим ближче | rв | до нуля, тим зв’язок слабший. За допомогою вибіркових характеристик
У випадку нелінійної кореляції параметри нелінійних рівнянь регресії шукають також методом найменших квадратів. Зокрема, у випадку параболічної кореляції другого порядку коефіцієнти a 0, a 1, а 2 вибіркового рівняння регресії Y на Х y = a 0 + a 1 x + a 2 x 2
знаходять із системи
Коефіцієнти вибіркового рівняння регресії Х на Y х = b 0 + b 1 y + b 2 y 2 знаходять з аналогічної системи рівнянь. Для оцінки сили нелінійної кореляційної залежності служать кореляційні відношення:
величини Х до випадкової величини Y, або їх вибіркові оцінки
де
Вважається, що при
Опитування з теорії
1.Яка залежність між двома випадковими величинами називається кореляційною? Дати означення функцій регресії двох випадкових величин. 2.Як встановлюють форму кореляційної залежності за вибірковими даними? Як знаходять параметри рівнянь регресії? 3.Записати вибіркові рівняння прямих регресії. 4.Записати формулу для обчислення вибіркового коефіцієнта кореляції. Які властивості має цей коефіцієнт? 5.Що таке кореляційні відношення двох випадкових величин? Які властивості вони мають? 6.Записати формули для обчислення вибіркових оцінок кореляційних відношень двох випадкових величин.
Задача 1. Результати лабораторних аналізів десяти зразків речовини щодо вмісту компонент X та Y (у відсотках) зведені в таблицю
Вважаючи залежність між випадковими величинами X та Y близькою до лінійної, знайти лінійні рівняння регресії Y на X та X на Y і обчислити вибірковий коефіцієнт кореляції. Розв¢язання. Для обчислення коефіцієнтів лінійних рівнянь регресії (12.4) та вибіркового коефіцієнта кореляції за формулами (12.2), (12.5), знаходимо потрібні суми.
Тепер за формулами (12.2) маємо:
Таким чином, лінійні рівняння регресії мають вигляд y = 2,5 x + 1,5- рівняння регресії Y на Х, x = 0,3629 y - 0,0806 - рівняння регресії Х на Y. Вибірковий коефіцієнт кореляції обчислюємо за формулою (12.5)
Задача 2. В кореляційній таблиці подані оцінки з вищої математики (Х) та фізики (Y), отримані студентами двох груп в екзаменаційну сесію. Вважаючи залежність між випадковими величинами Х та Y близькою до лінійної, знайти лінійні рівняння регресії Y на X та X на Y і обчислити вибірковий коефіцієнт кореляції.
Розв¢язання. Коефіцієнти лінійних рівнянь регресії (12.4) знаходимо за формулами (12.3). Для цього обчислюємо потрібні суми.
Аналогічно знаходимо інші суми:
Тепер за формулами (12.3) маємо
Таким чином, лінійні рівняння регресії мають вигляд y = 0,74 x + 1,16 - рівняння регресії Y на Х, x = 0,76 y - 0,81 - рівняння регресії Х на Y. Для знаходження вибіркового коефіцієнта кореляції обчислимо ще кілька сум.
Тепер за формулою (12.5) дістанемо
Задача 3. Результати вимірювань величин Х та Y наведені в кореляційній таблиці. Знайти вибіркову функцію регресії
Розв¢язання. Коефіцієнти b 0, b 1, b 2 вибіркової функції регресіїзнаходимо з системи, аналогічної системі (12.6)
Обчислюємо потрібні суми.
Аналогічно
Отже, система (12.8) має вигляд
190 b 0 + 800 b 1 + 3580 b 2 = 6946, 800 b 0 + 3580 b 1 + 16580 b 2 = 32394. Її розв¢язок, знайдений, наприклад, методом Гаусса, буде b 0 = - 22, b 1= 12,267, b 2= 0,367. Таким чином, вибіркова функція регресії X на Y має вигляд
Вибіркове кореляційне відношення
= 17102,3;
Отже, шукане вибіркове кореляційне відношення
Задачі для аудиторної та самостійної роботи
1. Знайти лінійні рівняння регресії Y на X та X на Y за вибірковими даними двовимірної випадкової величини (Х, Y):
Відповідь: а) y = – 1,06 x + 20,3; x = – 0,971 y + 19,477; б) y = 2. Обчислити вибірковий коефіцієнт кореляції і скласти лінійні рівняння регресії за вибіркою значень двовимірної випадкової величини:
д)
е)
Відповідь: a) rв = 0,92; y = 0,24 x + 5,42; x = 3,53 y – 11,56; б) rв = 0,455; y = 0,57 x + 22,51; x = 0,36 y + 37,2; в) rв = 0,75; y = 0,6 x + 1,73; x = 0,8 y + 0,79; г) rв = – 0,83; y = – 0,83 x + 1,2; x = – 0,77 y + 1,18; д) rв = 0,67; y = 5,16 x + 22,12; x = 0,09 y + 0,63; e) rв = – 0,62; y = – 0,45 x + 50,48; x = – 0,84 y + + 58,33.
3. Знайти вибіркову функцію регресії
Відповідь: a) 4. Знайти вибіркову функцію регресії
Відповідь: а)
Практичне заняття 13
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 863; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.103.57 (0.011 с.) |

 - функція регресії Y на Х,
- функція регресії Y на Х,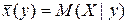 - функція регресії Х на Y.
- функція регресії Х на Y. та
та  .
.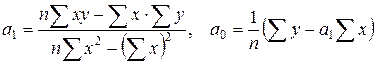 ,
, (12.2)
(12.2) пишемо
пишемо  ).
). ,
, 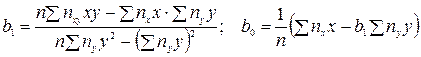 . (12.3)
. (12.3) - рівняння регресії Y на Х,
- рівняння регресії Y на Х, - рівняння регресії Х на Y; (12.4)
- рівняння регресії Х на Y; (12.4) - пряма регресії Y на Х,
- пряма регресії Y на Х, - пряма регресії Х на Y.
- пряма регресії Х на Y. (12.5)
(12.5) , sx, sy та вибіркового коефіцієнта кореляції rв рівняння прямих регресії записуються у такому вигляді
, sx, sy та вибіркового коефіцієнта кореляції rв рівняння прямих регресії записуються у такому вигляді
 (12.6)
(12.6) - кореляційне відношення випадкової величини Y до випадкової величини Х,
- кореляційне відношення випадкової величини Y до випадкової величини Х,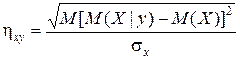 - кореляційне відношення випадкової
- кореляційне відношення випадкової ,
,  , (12.7)
, (12.7)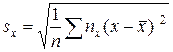 ,
,  ,
, ,
,  ,
, ,
,  .
. кореляційна залежність між Х і Y відсутня; якщо
кореляційна залежність між Х і Y відсутня; якщо  , між Y та Х існує майже функціональна залежність; при
, між Y та Х існує майже функціональна залежність; при  кореляційна залежність між Y та Х тісна.
кореляційна залежність між Y та Х тісна.
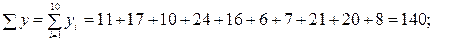


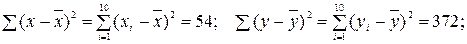
 .
. ;
; .
. .
.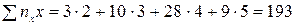 .
. .
. ;
; .
.


 .
. b 0 + + b 1 y + b 2 y 2та вибіркове кореляційне відношення
b 0 + + b 1 y + b 2 y 2та вибіркове кореляційне відношення  .
.
 (12.8)
(12.8)
 .
.
 .
. 50 b 0 + 190 b 1 + 800 b 2 = 1524,
50 b 0 + 190 b 1 + 800 b 2 = 1524,
 .
.
 =15(4 - 30,48)2+15(32,93 - 30,48)2+20(48,5 - 30,48)2 =
=15(4 - 30,48)2+15(32,93 - 30,48)2+20(48,5 - 30,48)2 =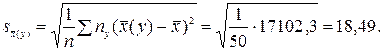
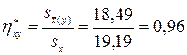 .
. а 1 х 2 + b 1 x + c 1 та вибіркове кореляційне відношення
а 1 х 2 + b 1 x + c 1 та вибіркове кореляційне відношення  за даними, наведеними в кореляційній таблиці:
за даними, наведеними в кореляційній таблиці: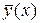 = 2,94 х 2+7,27 х – 1,25;
= 2,94 х 2+7,27 х – 1,25;  = 2,8 y 2+0,02 y + 3,18;
= 2,8 y 2+0,02 y + 3,18; 


