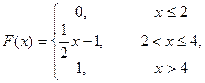Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Індивідуальні завдання з прикладної математики.Содержание книги
Поиск на нашем сайте
Модуль “Елементи теорії ймовірностей та математичної статистики”
ЗАДАЧА №1 1. Одночасно зроблено 3 постріли в мішень. Ймовірність того, що перший стрілець влучить у мішень дорівнює 0,7, другий - 0,8, третій - 0,85. Знайти ймовірність того, що: а) у ціль влучено; б) влучили 2 стрільці. 2. Незалежно один від одного працюють 4 прилади. Ймовірність того, що зіпсується перший прилад, дорівнює 0,2, другий - 0,15, третій - 0,1, четвертий - 0,25. Знайти ймовірність того, що працюють: а) усі прилади; б) тільки два. 3. Одночасно зроблено 4 постріли в мішень. Ймовірність того, що влучить перший стрілець, дорівнює 0,6, другий - 0,7, третій – 0,75, четвертий - 0,65. Знайти ймовірність того, що в ціль влучили: 4. Незалежно один від одного працюють 3 прилади. Ймовірність того, що працює перший прилад, дорівнює 0,8, другий - 0,7, третій - 0,75. Знайти ймовірність того, що зіпсуються: а) 2 прилади одночасно; б) усі прилади. 5. Зроблено постріл з трьох гармат одночасно. Ймовірність того, що в ціль не влучено з першої гармати, дорівнює 0,25, з другої- 05, з третьої - 0,2. Знайти ймовірність того, що: а) у ціль влучено; б) влучили не менше ніж 2 гармати. 6. Незалежно один від одного працюють 3 прилади. Ймовірність того, що зіпсується перший прилад, дорівнює 0,15, другий - 0,25, третій - 0,2. Знайти ймовірність того, що: а) жоден прилад не зіпсується; б) зіпсуються тільки 2 прилади. 7. Зроблено залп із чотирьох гармат. Ймовірність того, що не влучено в ціль з першої гармати, дорівнює 0,3, другої - 0,2, третьої - 0,25, четвертої - 0,1. Знайти ймовірність того, що: а) у ціль влучено; б) влучено хоча б з трьох гармат. 8. У ящику є деталі, виготовлені на трьох верстатах. Ймовір-ність того,що деталь виготовлено на першому верстаті, дорівнює 0,85, на друтому - 0,1 на третьому - 0,05. Навмання дістали 3 деталі. Знайти ймовірність того, що: а) усі деталі виготовлені на першому верстаті; б) тільки 2 виготовлені на першому верстаті. 9. Працюють 3 трактори. Ймовірність того, що перший трактор потребуватиме ремонту під час роботи, дорівнює 0,2, другий - 0, 3, третій - 0,35. Знайти ймовірність того, що: а) жоден трактор не потре-буватиме ремонту; б) потребуватиме ремонту тільки один трактор. 10. Чотири прилади працюють незалежно один від одного. Ймовірність того, що під час роботи не потребує ремонту перший прилад, дорівнює 0,7, другий - 0,8, третій - 0,75, четвертий - 0,9. Знайти ймовірність того, що потребує ремонту: а) тільки один прилад;
б) хоча б один. 11. Зроблено залп з трьох гармат. Ймовірність того, що в ціль влучили з першої гармати, дорівнює 0,75, з другої - 0,85, третьої - 0,6. Знайти ймовірність того, що в ціль влучили: а) хоча б дві гармати; б) тільки одна гармата. 12. Незалежно один від одного працюють 3 прилади. Ймовір-ність того, що перший прилад не потребує ремонту, дорівнює 0,9, другий - 0,8, третій - 0,85. Знайти ймовірність того, що не працює: а) жоден прилад; б) тільки один прилад. 13. Працюють 4 трактори. Ймовірність того, що під час робота потребує ремонту перший трактор, дорівнює 0,15, другий - 0,2, третій - 0,1, четвертий - 0,3. Знайти ймовірність того, що ремонту: а) не по-требують три трактори; б) потребує тільки один трактор. 14. Одночасно зробили постріл 4 гармати. Ймовірність того, що в ціль влучено з першої гармати, дорівнює 0,6, з другої - 0,65, з третьої - 0,75, із четвертої - 0,7. Знайти ймовірність того, що в ціль: а) не влучено; б) влучено тільки з двох гармат. 15. Три абоненти телефонують по черзі. Ймовірність додзвони-тися протягом двох хвилин для першого абонента дорівнює 0,8, для другого - 0,7, для третього - 0,9. Знайти ймовірність того, що додзво-няться: а) усі 3 абоненти; б) хоча б два абоненти. 16. Три прилади працюють незалежно один від одного. Ймовірність того, що не зіпсується перший прилад, дорівнює 0,9, другий - 0,8, третій - 0,75. Знайти ймовірність того, що працюють: а) не менше двох приладів; 6) хоча б два прилади. 17. У ящику є деталі, зроблені на трьох верстатах. Ймовірність того, що деталь зроблена на першому верстаті, дорівнює 0,7, на другому - 0,2, на третьому – 0,1. Виймають 3 деталі. Знайти ймовірність того, що: а) всі деталі зроблені на різних верстатах; б) 2 деталі зроблені на одному верстаті. 18. Зроблено 3 постріли одночасно. Ймовірність того, що влучив у ціль перший стрілець, дорівнює 0,65, другий - 0,8, третій - 0,75. 19. Працюють три трактори. Ймовірність того, що під час роботи не зіпсується перший трактор, дорівнює - 0,85, другий - 0,9, третій - 0,75. Знайти ймовірність того, що працюють: а) хоча б два трактори; б) тільки один трактор.
20. Зроблено незалежно один від одного 4 постріли по мішені. Ймовірність того, що в ціль не влучив перший стрілець, дорівнює 0,2, другий - 0,3, третій - 0,15, четвертий - 0,25. Знайти ймовірність того, що в ціль влучили: а) не менше двох стрільців; б) три стрільці. 21. Чотири прилади працюють незалежно один від одного. Ймовірність того, що зіпсується перший прилад, дорівнює 0,35, другий – 0,3, третій - 0,2, четвертий - 0,25. Знайти ймовірність того, що працюють: а) не менше трьох приладів; б) хоча б один прилад. 22. У ящику є деталі, зроблені на трьох верстатах. Ймовірність того, що деталь зроблена на першому верстаті, дорівнює 0,15, на другому - 0,15, на третьому - 0,6. Навмання виймають 4 деталі. Знайти ймовірність того, що: а) усі деталі зроблені на різних верстатах; б) 2 деталі зроблені на одному верстаті, 2 інші - на різних. 23. Незалежно один від одного працюють 4 прилади. Ймовір-ність того, що працює перший прилад, дорівнює 0,7, другий - 0,75, третій - 0,85, четвертий - 0,8. Знайти ймовірність того, що працю-ють: а) три прилади; б) не менше двох приладів. 24. Зроблено залп з трьох гармат. Ймовірність того, що в ціль влучено з першої гармати, дорівнює 0,75, з другої - 0,7, з третьої -0,9. Знайти ймовірність того, що в ціль влучили: а) не менше ніж з двох гармат; б) з трьох гармат. 25. Три трактори працюють у полі. Ймовірність того, що під час роботи потребуватиме ремонту перший трактор, дорівнює 0,1, другий - 0,25,третій - 0,2. Знайти ймовірність того, що під час роботи не зіпсується: а) два трактори; б) хоча б один трактор. 26. Чотири стрільці стріляють по мішені. Ймовірність того, що в ціль влучив перший стрілець, дорівнює 0,7, другий - 0,9, третій - 0,75, четвертий - 0,85. Знайти ймовірність того, що влучать: а) не менше двох стрільців; б) більше трьох стрільців. 27. У ящику є деталі, які виготовлені на трьох верстатах. Ймовірність того, що деталь виготовлена на першому верстаті, дорівнює 0,2, на другому - 0,05, на третьому - 0,75. Виймають 3 деталі. Знайти ймовірність того, що деталі виготовлені: а) одна на другому верстаті, дві інші - на різних верстатах; б) на різних верстатах. 28. Стріляють 3 стрільці одночасно і незалежно один від одного. Ймовірність того, що в ціль не влучить перший стрілець, дорівнює 0,25, другий - 0,3, третій - 0,35. Знайти ймовірність того, що: а) в ціль влучать 3 стрільці; б) у ціль влучать менше трьох. 29. В класі 18 хлопчиків і 12 дівчат. Яка ймовірність того, що з двох вибраних дітей: а) обидва хлопчики; б) один хлопчик і одна дівчинка. 30. Три прилади працюють незалежно один від одного. Ймовірність того, що працює перший прилад, дорівнює 0,8, другий - 0,85, третій - 0,95. Знайти ймовірність того, що не працює: а) тільки один прилад; б) хоча б один прилад.
ЗАДАЧА №2 1. Схожість насіння складає 90%. Посіяно 4 зернини. Знайти ймовірність того, що зійде: а) не менше ніж три зернини; б) хоча б одна зернина. 2. Прилад має 5 вузлів. Ймовірність того, що зіпсується кожен з них, дорівнює 0,2. Знайти ймовірність того, що зіпсуються: а) два вузли; б) не менше трьох вузлів. 3. Приживлюваність дерев складає 80 %. Знайти ймовірність того, що із 6 посаджених дерев приживуться: а) 4 дерева; б) більше трьох дерев. 4. Засміченість насіння 0,1 %. Знайти ймовірність того, що серед 3000 зернин насіння бур'янів складатиме: а) чотири зернини; б) не більше двох зернин. 5. Схожість насіння коноплі складає 70%. Знайти ймовір-ність того, що з 5 посіяних зернин зійдуть: а) не менше ніж 4 зернини; б) тільки 2 зернини.
6. Прилад складається з 1000 елементів. Ймовірність того, що зіпсується кожний з них, дорівнює 0,002. Знайти ймовірність того, що: а)зіпсуються 2 елементи; б) зіпсуються не менше трьох. 7. Схожість насіння цибулі складє 60%. Знайти ймовірність того, що із 6 посіяних зернин зійдуть: а) хоча б 5 зернин; б) не більше двох зернин. 8. Є 30000 примірників книги. Ймовірність того, що в книзі є дефект, дорівнює 0,0001. Знайти ймовірність того, що дефект є: а) менше ніж у трьох книгах; б) у п'яти книгах. 9. Ймовірність того, що зерно заражене хворобою в прихованій формі, дорівнює 0,002. Знайти ймовірність того, що з 1000 зернин незараженими будуть: а) 998 зернин; б) більше ніж 997 зернин. 10. Зараженість плодів складає 20%. Знайти ймовірність того, що із 7 відібраних плодів не зараженими будуть: а) 5 плодів; б) не менше шести плодів. 11. Ймовірність того, що деталь бракована, дорівнює 0,00025. Знайти ймовірність того, що серед 4000 деталей бракованими будуть: а) 2 деталі; б) менше ніж 3 деталі. 12. Засміченість насіння бур'янами складає 10 %. Знайти ймо-вірність того, що із шести навмання взятих зерен насінин основної культури буде: а) не менше ніж 5 зернин; б) хоча б одна зернина. 13. У книжці є 1000 сторінок. Друкарські помилки зустріча-ються на кожній сторінці з імовірністю 0,002. Знайти ймовірність того, що помилки зустрінуться: а) більше ніж на трьох сторінках; б) хоча б на одній сторінці. 14. Відомо, що приблизно 60% сімей мають телевізори. Знайти ймовірність того, що серед 5 сімей телевізори мають: а) не менше ніж 3 сім’ї, але не більше ніж 4 сім’ї; б) хоча б одна сім’я. 15. Насіння пшениці містить 0,2% насіння бур'янів. Знайти ймовірність того, що серед 1000 зерен зернин бур'янів буде: а) не менше ніж 2, але не більше ніж 4; б) хоча б одна зернина. 16. Ймовірність народження хлопчика і дівчинки однакова. Знайти ймовірність того, що в сім'ї, де шестеро дітей, буде: а) 3 хлопчики і 3 дівчинки; б) не менше ніж 3 хлопчики. 17. Комутатор обслуговує 200 абонентів. Ймовірність того, що абонент зателефонує протягом 10хв., дорівнює 0,01. Знайти ймовірність того, що протягом 10 хв. зателефонують: а) 2 абоненти; б) більше ніж 3 абоненти. 18. У ставку 80% риби - це коропи. Знайти ймовірність того, що серед шести виловлених риб коропів буде: а) не менше ніж 5; б) менше ніж 3. 19. Ймовірність того, що деталь бракована, дорівнює 0,008. Знайти ймовірність того, що серед 250 деталей бракованих буде: а) не більше ніж 2; б) тільки 2.
20. Схожість насіння складає 70%. Знайти ймовірність того, що серед шести посіяних зернин зійде: а) не менше ніж 5; б) не більше ніж 2. 21. Ймовірність того, що в приладі зіпсується будь-який один елемент, дорівнює 0,004. Знайти ймовірність того, що серед 500 елементів зіпсуються: а) не більше двох елементів; б) більше чотирьох елементів. 22. Відбираються 7 приладів. Ймовірність того, що в кожному з них є дефект, дорівнює 0,2. Знайти ймовірність того, що дефект не мають: а) 2 прилади; б) не менше трьох. 23. Ймовірність того, що деталь буде бракованою, дорівнює 0,004. Знайти ймовірність того, що в партії з 500 деталей бракованих буде: а)менше двох; б) більше трьох. 24. Ймовірність того, що протягом дня буде перевищена норма користування електроенергією, дорівнює 0,3. Знайти ймовірність того, що із 6 користувачів перевищать цю норму: а) більше 5; б) не більше чотирьох. 25. Протягом 10 хвилин кожен із 100 абонентів може зателефонувати з імовірністю 0,02. Знайти ймовірність того, що зателефонують: а) 3 абоненти; б) більше ніж 4 абоненти. 26. Схожість насіння кукурудзи складає 80%. Знайти ймовірність того, що з 5 посіяних зернин зійде: а) не менше ніж 4 зернини; б) менше ніж 2 зернини. 27. У книжці є 2000 сторінок. Ймовірність того, що на кожній сторінці є друкарські помилки, становить 0,1%. Знайти ймовірність того, що помилки є на: а) одній сторінці; б) більше ніж на одній сторінці. 28. Приживлюваність саджанців груші складає 70 %. Знайти ймовірність того, що із чотирьох посаджених дерев приживуться: а) 3 саджанці; б) більше ніж один саджанець. 29. Ймовірність виживання бактерій дорівнює 0,008. Знайти ймовірність того, що з 500 бактерій виживуть: а) дві бактерії; б) не менше трьох бактерій. 30. Приживлюваність саджанців аґрусу - 85 %. Знайти ймо-вірність того, що з 5 посаджених кущів приживуться: а) не менше чотирьох кущів; б) хоча б три кущі.
ЗАДАЧА №3 Ймовірність того, що деталь першого сорту дорівнює р. Зроблено n деталей. Знайти ймовірність того, що серед них m деталей першого сорту.
ЗАДАЧА №4 Відділ технічного контролю перевіряє партію деталей. Ймовірність того, що деталь стандартна дорівнює р. Знайти ймовірність того, що з n перевірених деталей стандартних буде не менше ніж m 1 і не більше ніж m 2.
ЗАДАЧА №5 Задано закон розподілу дискретної випадкової величини. Знайти математичне сподівання, дисперсію, середнє квадратичне відхилення, інтегральну функцію розподілу F (x) цієї випадкової величини.
ЗАДАЧА №6 Неперервна випадкова величина задана інтегральною функцією розподілу (непарні варіанти) або диференціальною функцією розподілу - щільністю (парні варіанти). Знайти: 1) диференціальну функцію розподілу – щільність (непарні варіанти) або інтегральну функцію розподілу (парні варіанти); 2) ймовірність того, що випадкова величина потрапить у заданий інтервал (
ЗАДАЧА №7 Задана рівномірно розподілена в інтервалі (a,b) неперервна випадкова величина Х. Знайти: 1) числові характеристики: мате-матичне сподівання, дисперсію, середнє квадратичне відхилення; 2) інтегральну функцію розподілу; 3) побудувати графіки диференціальної і інтегральної функцій розподілу.
ЗАДАЧА №8 Деталі, що їх випускає цех, розподілені за розміром діаметра по нормальному закону. Стандартний розмір деталі (математичне споді-вання) дорівнює a мм, середнє квадратичне відхилення s мм. Знайти: 1) ймовірність того, що діаметр будь-якої взятої деталі буде більший ніж a мм і менший, ніж bмм; 2) ймовірність того, що діаметр деталі відхиляється від стандартної величини не більше, ніж на d мм.
ЗАДАЧА №9 Для дослідження неперервної ознаки X генеральної сукупності зроблено вибірку. Необхідно: 1) скласти статистичний розподіл вибірки, розбивши значення Х на 5 інтервалів; 2) побудувати гісто-граму відносних частот; 3) знайти незміщені оцінки генеральної середньої та генеральної дисперсії; 4) знайти з надійністю 0,95 надій-ний інтервал для математичного сподівання а нормально розподіленої ознаки Х генеральної сукупності.
ЗАДАЧА №10 Знайти коефіцієнт кореляції двох випадк
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 696; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.159.163 (0.014 с.) |

 ); 3) матема-тичне сподівання, дисперсію, середнє квадратичне відхилення; 4) на-креслити графіки інтегральної і диференціальної функцій розподілу.
); 3) матема-тичне сподівання, дисперсію, середнє квадратичне відхилення; 4) на-креслити графіки інтегральної і диференціальної функцій розподілу. )
)