
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Побудова довірчого інтервалу для середнього квадратичного відхиленняСодержание книги
Поиск на нашем сайте
Нехай кількісна ознака Х розподілена за нормальним законом з параметрами На підставі вибірки знайдемо точкові оцінки параметрів а і ступенями свободи. Знайдемо значення
де
Опитування з теорії
1.Яка статистична оцінка називається інтервальною? 2.Що називається довірчою ймовірністю (надійністю) статистичної оцінки? 3.Як визначити довірчий інтервал дляматематичного сподівання нормального розподілу при відомому середньому квадратичному відхиленні 4.Як можна підвищити точність статистичної оцінки? 5. За якою формулою знаходиться мінімальний об’єм вибірки для оцінки математичного сподівання з наперед заданою точністю 6. Як знайти довірчийінтервал для математичного сподівання нормального розподілупри невідомомусередньому квадратичному відхиленні 7. Як будується довірчий інтервал для середнього квадратичного відхилення?
Задача 1. Одним і тим самим приладом проведено 25 рівноточних вимірювань фізичної величини із середнім квадратичним відхиленням випадкових похибок вимірювання Розв’язання. Визначимо число Задача 2. Знайти мінімальний об’єм вибірки з генеральної сукупності, при якому з надійністю Розв’язання. Знайдемо об’єм вибірки, використовуючи формулу Задача 3. За даними 16 незалежних вимірювань деякої фізичної величини з відомим середнім квадратичним відхиленням Розв’язання. З умови Задача 4. Отримано 36 значень нормально розподіленої величини Х з відомим середнім квадратичним відхиленням Розв’язання. Визначимо число Задача 5. За даними дев’яти вимірювань деякої фізичної величини знайдені середнє арифметичне результатів вимірювань
Розв’язання. Для знаходження довірчого інтервалу для істинного значення фізичної величини знайдемо величину Задача 6. З нормально розподіленої генеральної сукупності зроблена вибірка об’єму
Оцінити математичне сподівання з надійністю Розв’язання. Знайдемо середнє арифметичне виправлену дисперсію і виправлене середнє квадратичне відхилення
Для знаходження довірчого інтервалу для математичного сподівання знайдемо величину Задача 7. Випадкова величина розподілена за нормальним законом. На підставі Розв’язання. Для побудови довірчого інтервалу знайдемо виправлене середнє квадратичне відхилення Задача 8. У відділі технічного контролю були виміряні діаметри 20 втулок, що виготовлені одним станком-автоматом. Результати відхилення (в мікронах) від номіналу представлені в таблиці
Знайти довірчі інтервали для оцінки з надійністю 0,9 дисперсії і середнього квадратичного відхилення результатів вимірювання. Розв’язання. За вибіркою знайдемо вибіркову середню виправлену дисперсію і виправлене середнє квадратичне відхилення
Шуканий довірчий інтервал, що покриває невідому дисперсію
Шуканий довірчий інтервал, що покриває невідоме середнє квадратичне відхилення Задача 9. За даними вибірки об’єму Розв’язання. За довірчою ймовірністю
Задача 10. Результати вимірювання ваги 20 випадково відібраних підлітків мають вигляд
Знайти довірчі інтервали, що покривають математичне сподівання і середнє квадратичне відхилення з надійністю 0,95(за варіанти вибірки взяти середини інтервалів).
Розв’язання. Представимо вибірку у вигляді розподілу частот
Знайдемо вибіркову середню і виправлене середнє квадратичне відхилення:
Знайдемо довірчий інтервал для математичного сподівання Знайдемо довірчий інтервал для середнього квадратичного відхилення
Маємо Задача 11. Проведено 16 вимірювань одним приладом (без систематичних похибок) деякої фізичної величини, причому виправлене середнє квадратичне відхилення похибок вимірювання виявилось рівним 0,5. Знайти точність приладу (Вказівка. Для знаходження точності приладу потрібно відшукати довірчий інтервал для середнього квадратичного відхилення). Розв’язання. Знайдемодовірчий інтервал для середнього квадратичного відхилення
Задача 12. Для визначення врожайності пшениці проводились її вибіркові вимірювання на 20 ділянках. Результати вимірювань наведе-ні нижче. Знайти довірчі інтервали з надійністю 0,95 для генеральної середньої та генерального середнього квадратичного відхилення. 21,0; 23,4; 20,0; 25,6; 21,4; 22,5; 22,8; 22,3; 24,9; 22,9; 22,4; 23,6; 20,9; 23,8; 21,8; 21,3; 23,4; 23,2; 24,3; 25,2. Розв’язання. Розіб’ємо результати вимірювань на 6 інтервалів і відмітимо частоту попадання в кожний інтервал. Дані зведемо в таблицю
Виберемо за варіанти середини інтервалів:
Знайдемо вибіркову середню і виправлене середнє квадратичне відхилення:
Знайдемо довірчий інтервал для математичного сподівання
Задачі для аудиторної та самостійної роботи
1. Одним і тим самим приладом проведено 36 рівноточних вимірювань фізичної величини із середнім квадратичним відхиленням випадкових похибок вимірювання 2. Знайти мінімальний об’єм вибірки з генеральної сукупності, при якому з надійністю 3. За даними 25 незалежних вимірювань деякої фізичної величини з відомим середнім квадратичним відхиленням 4. Отримано 16 значень нормально розподіленої величини Х з відомим середнім квадратичним відхиленням 5. За даними десяти вимірювань деякої фізичної величини знайдені середнє арифметичне результатів вимірювань 6. З нормально розподіленої генеральної сукупності зроблена вибірка об’єму
Оцінити математичне сподівання з надійністю 7. Випадкова величина розподілена за нормальним законом. На підставі Відповідь: 8. У відділі технічного контролю були виміряні діаметри 25 втулок, що виготовлені одним станком-автоматом. Результати відхилення (в мікронах) від номіналу представлені в таблиці
Знайти довірчі інтервали для оцінки з надійністю 0,9 дисперсії і середнього квадратичного відхилення результатів вимірювання. Відповідь: 9. За даними вибірки об’єму 10. Результати вимірювання ваги 30 випадково відібраних підлітків мають вигляд
Знайти довірчі інтервали, що покривають математичне сподівання і середнє квадратичне відхилення з надійністю 0,95 (за варіанти вибірки взяти середини інтервалів). Відповідь: 11. Проведено 25 вимірювань одним приладом (без систематичних похибок) деякої фізичної величини, причому виправлене середнє квадратичне відхилення похибок вимірювання виявилось рівним 0,8. Знайти точність приладу (Вказівка. Для знаходження точності приладу потрібно відшукати довірчий інтервал для середнього квадратичного відхилення). Відповідь: 12. Для визначення врожайності пшениці проводились її вибіркові вимірювання на 20 ділянках. Результати вимірювань приведені нижче. Знайти довірчі інтервали з надійністю 0,95 для генеральної середньої та генерального середнього квадратичного відхилення. 21,4; 22,6; 22,4; 22,8; 20,8; 23,7; 22,4; 22,2; 23,3; 24,2; 23,50; 22,4; 21,9; 24,6; 20,4; 21,5; 21,8; 21,3; 23,9; 21,9. (Вказівка. Результати вимірювань розбити на 5 інтервалів: 20-21, 21-22, 22-23, 23-24, 24-25 і вибрати за варіанти середини інтервалів). Відповідь:
Практичне заняття 11
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 1262; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.42.174 (0.007 с.) |

 , причому параметри а і
, причому параметри а і  невідомі.
невідомі. , де
, де  – виправлене середнє квадратичне відхилення. Доведено, що випадкова величина
– виправлене середнє квадратичне відхилення. Доведено, що випадкова величина  розподілена за законом
розподілена за законом 
 , виходячи з умов
, виходячи з умов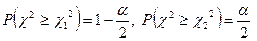 , (10.3)
, (10.3) (
( – довірча ймовірність). Розв’язавши рівняння (10.3) за допомогою таблиці критичних точок розподілу
– довірча ймовірність). Розв’язавши рівняння (10.3) за допомогою таблиці критичних точок розподілу 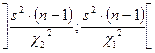 , що з надійністю
, що з надійністю  , який з надійністю
, який з надійністю  і надійністю
і надійністю  . Знайти довірчий інтервал для математичного сподівання
. Знайти довірчий інтервал для математичного сподівання  , якщо вибіркова середня
, якщо вибіркова середня  . Вважати, що результати вимірювання розподілені нормально. Довірчу ймовірність прийняти за
. Вважати, що результати вимірювання розподілені нормально. Довірчу ймовірність прийняти за  .
. за допомогою таблиці значень функції Лапласа з умови
за допомогою таблиці значень функції Лапласа з умови 

 . Знаходимо
. Знаходимо  . Тепер обчислимо точність оцінки
. Тепер обчислимо точність оцінки  . Отже, шуканий довірчий інтервал
. Отже, шуканий довірчий інтервал 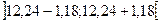 або
або  з надійністю
з надійністю 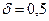 , якщо відоме середнє квадратичне відхилення
, якщо відоме середнє квадратичне відхилення  . Вважати, що генеральна сукупність нормально розподілена.
. Вважати, що генеральна сукупність нормально розподілена. . Визначимо число
. Визначимо число  . Оскільки об’єм вибірки ціле число, потрібно взяти число n =10.
. Оскільки об’єм вибірки ціле число, потрібно взяти число n =10. знайдена вибіркова середня 25,64. Оцінити істинне значення вимірю- ваної величини з допомогою довірчого інтервалу з надійністю
знайдена вибіркова середня 25,64. Оцінити істинне значення вимірю- ваної величини з допомогою довірчого інтервалу з надійністю  , вважаючи що істинне значення співпадає з математичним сподіван- ням. Вважається, що результати вимірювань розподілені нормально.
, вважаючи що істинне значення співпадає з математичним сподіван- ням. Вважається, що результати вимірювань розподілені нормально.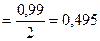 знаходимо
знаходимо  . Тепер обчислимо точність оцінки
. Тепер обчислимо точність оцінки  . Отже, шуканий довірчий інтервал
. Отже, шуканий довірчий інтервал  або
або  з надійністю
з надійністю 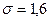 . Задана точність
. Задана точність  , з якою потрібно оцінити математичне сподівання за допомогою довірчого інтервалу. Встановити надійність
, з якою потрібно оцінити математичне сподівання за допомогою довірчого інтервалу. Встановити надійність  такої інтервальної оцінки.
такої інтервальної оцінки. , де
, де  – задані числа. Маємо
– задані числа. Маємо  . За допомогою таблиці зна- чень функції Лапласа знайдемо
. За допомогою таблиці зна- чень функції Лапласа знайдемо 
 . Отже, довірчий інтер-вал довжини
. Отже, довірчий інтер-вал довжини  з надійністю
з надійністю  покриває математичне сподівання.
покриває математичне сподівання. та виправлене середнє квадратичне відхилення
та виправлене середнє квадратичне відхилення  . Оцінити істинне значення фізичної величини з надійністю
. Оцінити істинне значення фізичної величини з надійністю  за відомими
за відомими  (див. таблицю розподілу Стьюдента, Додаток 3):
(див. таблицю розподілу Стьюдента, Додаток 3):  . Довірчий інтервал має вигляд
. Довірчий інтервал має вигляд 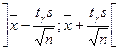 або
або  , тобто
, тобто  . Цей інтервал з надійністю
. Цей інтервал з надійністю  , що має вигляд
, що має вигляд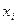

 ,
,
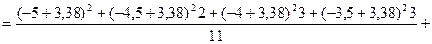
 ;
;  .
. . Довірчий інтервал має вигляд
. Довірчий інтервал має вигляд  , тобто
, тобто  .
. вимірювань знайдені середнє арифметичне результатів вимірювань
вимірювань знайдені середнє арифметичне результатів вимірювань  та вибіркова дисперсія
та вибіркова дисперсія 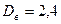 . Знайти довірчий інтервал для математичного сподівання з надійністю
. Знайти довірчий інтервал для математичного сподівання з надійністю  . Знайдемо величину
. Знайдемо величину  . Довірчий інтервал має вигляд
. Довірчий інтервал має вигляд  , тобто
, тобто  .
. ,
,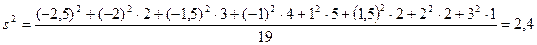 ,
,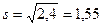 . За довірчою ймовірністю
. За довірчою ймовірністю  знайдемо
знайдемо  . За допомогою таблиці критичних точок розподілу
. За допомогою таблиці критичних точок розподілу  (Додаток 5) розв’язуємо рівняння (
(Додаток 5) розв’язуємо рівняння ( )
)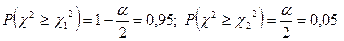 . Знаходимо
. Знаходимо  .
. :
: або
або  .
. .
. з нормально розподіленої генеральної сукупності знайдено виправлене середнє квадратичне відхилення
з нормально розподіленої генеральної сукупності знайдено виправлене середнє квадратичне відхилення  знайдемо
знайдемо  . За допомогою таблиці критичних точок розподілу
. За допомогою таблиці критичних точок розподілу  )
) . Знаходимо
. Знаходимо 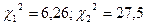 . Довірчий інтервал має вигляд
. Довірчий інтервал має вигляд або
або  .
. ,
,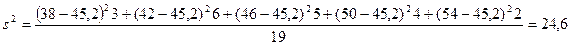
 .
.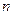 і
і  , звідки маємо
, звідки маємо 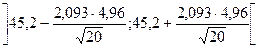 або
або  .
. шукається з рівнянь
шукається з рівнянь 
 – довірчий інтервал для середнього квадратичного відхилення.
– довірчий інтервал для середнього квадратичного відхилення. Після підстановки даних в довірчі межі отримаємо
Після підстановки даних в довірчі межі отримаємо  або
або 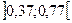 . Точність приладу лежить в межах
. Точність приладу лежить в межах  . Можна вважати, що дані приладу вірні з точністю до однієї поділки шкали вимірювання.
. Можна вважати, що дані приладу вірні з точністю до однієї поділки шкали вимірювання. ;
;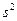

 ;
;  .
. або
або  – довірчий інтервал для математичного сподівання. Знайдемо довірчий інтервал для середнього квадратичного відхилення
– довірчий інтервал для математичного сподівання. Знайдемо довірчий інтервал для середнього квадратичного відхилення 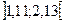 – довірчий інтервал для середнього квадратичного відхилення.
– довірчий інтервал для середнього квадратичного відхилення. . Знайти довірчий інтервал для математичного сподівання
. Знайти довірчий інтервал для математичного сподівання  . Вважати, що результати вимірювання розподілені нормально. Довірчу ймовірність прийняти за
. Вважати, що результати вимірювання розподілені нормально. Довірчу ймовірність прийняти за  .
. , якщо відоме середнє квадратичне відхилення
, якщо відоме середнє квадратичне відхилення  . Вважати, що генеральна сукупність нормально розподілена. Відповідь:
. Вважати, що генеральна сукупність нормально розподілена. Відповідь: 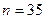 .
. знайдена вибіркова середня 5,44. Оцінити істинне значення вимірюваної величини з допомогою довірчого інтервалу з надійністю
знайдена вибіркова середня 5,44. Оцінити істинне значення вимірюваної величини з допомогою довірчого інтервалу з надійністю  .
. . Задана точність
. Задана точність  , з якою потрібно оцінити математичне сподівання за допомогою довірчого інтервалу. Встановити надійність
, з якою потрібно оцінити математичне сподівання за допомогою довірчого інтервалу. Встановити надійність  та виправлене середнє квадратичне відхилення
та виправлене середнє квадратичне відхилення  . Оцінити істинне значення фізичної величини з надійністю
. Оцінити істинне значення фізичної величини з надійністю  .
. , що має вигляд
, що має вигляд .
. та вибіркова дисперсія
та вибіркова дисперсія  . Знайти довірчий інтервал для математичного сподівання з надійністю
. Знайти довірчий інтервал для математичного сподівання з надійністю  .
. .
. .
. Вага(кг)
Вага(кг)
 .
.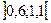 .
. .
.


