
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закони розподілу та основні характеристикиСодержание книги
Поиск на нашем сайте
ВИПАДКОВИХ ПРОЦЕСІВ. СТАЦІОНАРНІ ВИПАДКОВІ ПРОЦЕСИ
Випадкова функція і випадковий процес Випадкова функція – функція, яка залежно від результату (наслідку) випадкового експерименту приймає той чи інший конкретний вигляд.
Вигляд, який функція приймає в результаті досліду, називається реалізацією випадкової функції. Випадкова функція є функцією елементарної події, яка відбувається при здійсненні експерименту. Реалізація випадкової функції є невипадковою.
Випадковий процес – це випадкова функція, кожна реалізація якої є функція часу. Випадковий процес можна розглядати як функцію двох змінних – елементарної події При Випадкові процеси, в яких множина Т злічена, називаються процесами з дискретним часом. Якщо Т є інтервалом, то маємо процес з неперервним часом. Якщо
називається одновимірною функцією розподілу випадкового процесу, або одновимірним законом розподілу випадкового процесу.
Похідна одновимірної функції розподілу по
Двовимірний закон розподілу є сумісною функцією розподілу двох перерізів випадкового процесу, взятих відповідно для моментів
п - вимірним законом розподілу випадкового процесу
яка для будь-яких фіксованих значень
Як правило, в інженерних застосуваннях обмежуються одновимірним, інколи – двовимірним законом розподілу випадкового процесу. Крім того, при розв’язанні багатьох практичних задач взагалі відмовляються від законів розподілу випадкового процесу, а використовують його основні характеристики, аналогічні числовим характеристикам випадкових величин.
Числові характеристики випадкового процесу Математичним сподіванням випадкового процесу
Якщо при даному
то його математичне сподівання обчислюється за формулою
Якщо при даному
Наближено значення математичного сподівання обчислюється за формулою:
якщо отримано п реалізацій
Дисперсією випадкового процесу
Якщо переріз випадкового процесу
або
Якщо переріз випадкового процесу
або
Наближене значення дисперсії
або
Середнім квадратичним відхиленням випадкового процесу
Розмірність
Розглянуті характеристики mx (t), Dx (t) та s x (t) випадкового процесу X (t) визначаються одновимірним законом розподілу і не є вичерпними: вони не дозволяють описувати внутрішню структуру випадкового процесу.
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 325; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.31.251 (0.009 с.) |

 і часу
і часу 
 .
. випадковий процес перетворюється у випадкову величину
випадковий процес перетворюється у випадкову величину  , яка називається перерізом випадкового процесу.
, яка називається перерізом випадкового процесу. – випадковий процес і при
– випадковий процес і при 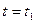 є випадковою величиною
є випадковою величиною  , то функція розподілу
, то функція розподілу (1.1)
(1.1)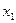 називається одновимірною щільністю розподілу випадкового процесу.
називається одновимірною щільністю розподілу випадкового процесу. і
і 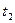 :
: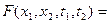
 . (1.2)
. (1.2)
 , (1.3)
, (1.3) , що належать множині Т, є (інтегральною) функцією розподілу п- вимірної випадкової величини (
, що належать множині Т, є (інтегральною) функцією розподілу п- вимірної випадкової величини ( ).
). , яка при кожному значенні аргументу
, яка при кожному значенні аргументу  . (1.4)
. (1.4)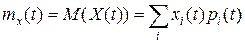 . (1.6)
. (1.6) . (1.7)
. (1.7) , (1.8)
, (1.8)
 випадкового процесу.
випадкового процесу. , яка при кожному значенні аргументу
, яка при кожному значенні аргументу  . (1.9)
. (1.9) , (1.10)
, (1.10) . (1.11)
. (1.11)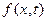 , то її дисперсія обчислюється за формулами:
, то її дисперсія обчислюється за формулами: , (1.12)
, (1.12)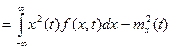 . (1.13)
. (1.13)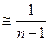
 , (1.14)
, (1.14) . (1.15)
. (1.15)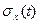 , яка визначається рівністю:
, яка визначається рівністю: . (1.16)
. (1.16)


