
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числові характеристики дискретної випадкової величиниСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Нехай Х – випадкова величина, яка може набувати значень Математичнимсподіванням випадкової величини Х називається сума ряду Дисперсією випадкової величини називається математичне сподівання квадрата різниці випадкової величини і її математичного сподівання:
Дисперсія дискретної випадкової величини має вигляд Середнім квадратичним відхиленням називається корінь квадратний з дисперсії випадкової величини Дисперсія і середнє квадратичне відхилення є мірою розсіювання випадкової величини навколо її математичного сподівання.
Основні закони розподілу дискретних випадкових величин 1 .Індикатор випадкової події А. Проводиться випадковий експеримент, в якому може відбутись випадкова подія А з імовірністю р. Випадкова величина Розподіл
2. Рівномірний розподіл. Дискретна випадкова величина 3. Біномний розподіл. Проводиться серія з п випробувань, в кожному з яких може відбутись подія А з імовірністю р. Випадкова величина Х – число настання події А. Її розподіл:
де 4. Розподіл Пуассона. Випадкова величина Х має розподіл Пуассона, якщо її розподіл має вигляд
де 5. Геометричний розподіл. Проводяться незалежні випробування, в кожному з яких може відбутись подія А зімовірністю р. Випадкова величина Х – число проведених випробувань до першого настання події А.
6. Гіпергеометричний розподіл. Нехай в партії з
Опитування з теорії
1. Дати означення випадкової величини. 2. Яка випадкова величина називається дискретною? 3. Як задають розподіл дискретної випадкової величини? 4. Що таке функція розподілу (інтегральна функція розподілу) випадкової величини? 5. Навести основні закони розподілу дискретної випадкової величини. 6. Які основні числові характеристики дискретної випадкової величини? Дати їх означення.
Задача1. Підкидається монета один раз. Скласти таблицю розподілу випадкової величини Розв’язання. Якщо монета підкидається один раз, то герб може випасти один раз або ні разу, тому
Тут Задача 2. Підкидається гральний кубик. Скласти таблицю розподілу випадкової величини Розв’язання. Дискретна випадкова величина
Це рівномірний розподіл. Задача 3. В партії з 10 деталей є 5 стандартних. Навмання вибирають 3 деталі. Знайти розподіл випадкової величини Х – кількість стандартних деталей серед 3 відібраних. Розв’язання. Х може приймати такі значення: 0, 1, 2, 3. Якщо
Тут маємо гіпергеометричний розподіл. Задача 4. Монета підкидається, поки не випаде герб. Знайти розподіл випадкової величини Розв’язання. Х може приймати такі значення: 0, 1, 2, …(цілі невід’ємні числа). Якщо
Це геометричний розподіл. Задача 5. Гральний кубик підкидається 5 разів. Знайти розподіл випадкової величини Х – кількість випадань 6 очок. Розв’язання. Випадкова величина Х може приймати такі значення: 0, 1, 2, 3, 4, 5. Якщо
Це біномний розподіл. Задача 6. Завод виробляє 90% деталей першого сорту і 10% деталей другого сорту. Навмання відбирається партія із 1000 деталей. Нехай Розв’язання. Враховуючи, що це біномний розподіл і подія “ А – деталь першого сорту” має ймовірність
Задача 7. Випадкова величина Х має рівномірний розподіл:
Побудувати функцію розподілу Х; знайти розподіл випадкової величини Розв’язання. Функцію розподілу випадкової величини Х будуємо так: якщо F (x)=2/3;при х >1 F (x)=1. Графік функції розподілу має вигляд
Знайдемо розподіл випадкової величини Задача 8. Дискретна випадкова величина Розв’язання. Підставимо у формулу розподілу Пуассона Задача 9. Гральний кубик підкидається, поки не випаде число очок, кратне трьом. Знайти розподіл випадкової величини Х – кількість підкидань до появи числа очок, кратного 3. Розв’язання. Нехай подія А – випало число очок, кратне 3. Подія А відбувається, якщо випаде число очок 3 або 6, її ймовірність – сума ймовірностей випадання 3 і 6, тобто
Задача 10. Три рази підкидається гральний кубик. Знайти розподіл випадкової величини Розв’язання. Тут ми маємо біномний розподіл, подія А –випадання 6 очок, Задача 11. Випадкова величина Х набуває значень Розв’язання. За означенням Очевидно, що тут є доданки, рівні за абсолютною величиною і з протилежними знаками, вони знищуються і Задача 12. Випадкова величина Х має розподіл
Знайти: 1) Розв’язання. 1)
2) 3) Випадкова величина
Задачі для аудиторної та самостійної роботи 1. Випадкова величина Х має розподіл
Обчислити: 1) Відповідь: 2. Випадкова величина має розподіл
Обчислити 3. Нехай випадкова величина має розподіл
Знайти розподіл випадкової величини Відповідь:
4. Нехай один раз підкидається гральний кубик. Знайти розподіл випадкової величини Х, де Х – індикатор події А «поява простого числа очок» і обчислити Відповідь:
5. Нехай 3 рази підкидається монета. Знайти розподіл випадкової величини Х – числа гербів при трьох підкиданнях, обчислити Відповідь:
6. Двічі підкидається гральний кубик. Знайти розподіл випадкової величини Х, де Х – число появ парного числа очок (біномний розподіл). Відповідь:
7. В урні 4 білих і 6 чорних куль. Навмання взяли одну кулю. Знайти розподіл випадкової величини Х – числа взятих білих куль; побудувати функцію розподілу (індикатор події). Відповідь:
8. В урні 4 білих і 6 чорних куль. Навмання взяли три кулі. Знайти розподіл випадкової величини Х – числа взятих білих куль (гіпергеометричний розподіл). Відповідь:
9. В урні 4 білих і 6 чорних куль. Навмання беруть одну кулю, якщо вона не біла, то її повертають в урну і беруть ще раз і т.д. Знайти розподіл випадкової величини Х – числа взятих куль до появи білої кулі (геометричний розподіл). Відповідь:
10. По мішені стріляють з гармати. Ймовірність попадання в мішень 0,7. Знайти розподіл випадкової величини Х – числа пострілів до першого попадання в мішень (геометричний розподіл ). Відповідь:
11. Випадкова величина Х має розподіл Пуассона з параметром Відповідь: 12. В партії 10% нестандартних виробів. Навмання відібрали 5 виробів. Знайти розподіл випадкової величини Х – числа нестандартних виробів серед 5 відібраних; обчислити
Практичне заняття 6
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 988; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.25.125 (0.007 с.) |

 з імовірностями
з імовірностями  (і= 1, 2, …). Припустимо, що ряд
(і= 1, 2, …). Припустимо, що ряд  збіжний.
збіжний. . У випадку, якщо
. У випадку, якщо 
 , кажуть, що випадкова величина не має математичного сподівання.
, кажуть, що випадкова величина не має математичного сподівання. .
.

 , яка приймає значення 1, якщо подія А відбулась, і значення 0, якщо подія А не відбулась, називається індикатором події А.
, яка приймає значення 1, якщо подія А відбулась, і значення 0, якщо подія А не відбулась, називається індикатором події А. може набувати значень
може набувати значень 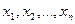 з однаковими ймовірностями
з однаковими ймовірностями  .
.


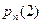


 ,
, 




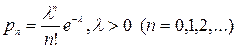 , причому
, причому 



 виробів
виробів  стандартних (
стандартних ( ). З партії навмання беруть
). З партії навмання беруть  виробів. Випадкова величина Х – число стандартних виробів серед
виробів. Випадкова величина Х – число стандартних виробів серед  з такими ймовірностями
з такими ймовірностями  .
.
 . Таблиця розподілу
. Таблиця розподілу , то вибрані 3 деталі нестандартні, яких всього є 5. Тому
, то вибрані 3 деталі нестандартні, яких всього є 5. Тому  .
. , то вибрали 1 стандартну і 2 нестандартних деталі. Тому
, то вибрали 1 стандартну і 2 нестандартних деталі. Тому  Якщо
Якщо  , то вибрали 2 стандартні і 1 нестандартну деталі. Відповідна ймовірність
, то вибрали 2 стандартні і 1 нестандартну деталі. Відповідна ймовірність  Якщо
Якщо  , то 3 вибраних деталі стандартні і
, то 3 вибраних деталі стандартні і  Таблиця розподілу:
Таблиця розподілу: . Якщо
. Якщо 
 . Якщо
. Якщо  . Якщо
. Якщо  , то при перших
, то при перших  (наступному) підкиданні – герб, тому
(наступному) підкиданні – герб, тому  . Таблиця розподілу:
. Таблиця розподілу:
 , тому
, тому  . Якщо
. Якщо  . Якщо
. Якщо  . Аналогічно,
. Аналогічно, 
 . Якщо
. Якщо  , то всі 5 разів випаде 6, тому
, то всі 5 разів випаде 6, тому  . Таблиця розподілу:
. Таблиця розподілу: і
і  , знаходимо
, знаходимо
 .
. , її математичне сподівання і дисперсію
, її математичне сподівання і дисперсію  (
( то F (x)=0; при -1< x £0 F (x)=1/3; при 0< x £1
то F (x)=0; при -1< x £0 F (x)=1/3; при 0< x £1

 . Знайдемо математичне сподівання і дисперсію
. Знайдемо математичне сподівання і дисперсію 

 . Знайти ймовірності того, що
. Знайти ймовірності того, що  .
. . Шукана ймовірність
. Шукана ймовірність  . Підставляючи значення
. Підставляючи значення  і склавши відповідні ймовірності, маємо
і склавши відповідні ймовірності, маємо  .
. Значить, ймовірність протилежної події
Значить, ймовірність протилежної події  Якщо Х =0, це означає,що відразу випало 3 або 6 з імовірністю
Якщо Х =0, це означає,що відразу випало 3 або 6 з імовірністю  . Якщо Х =1, то перший раз випало число очок,що не ділиться на 3 з імовірністю
. Якщо Х =1, то перший раз випало число очок,що не ділиться на 3 з імовірністю 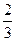 , другий раз випало число очок, що ділиться на 3 з імовірністю
, другий раз випало число очок, що ділиться на 3 з імовірністю  Якщо
Якщо 
 , це означає, що
, це означає, що  раз випало число очок, що не ділиться на 3 і після цього випало число очок кратне 3, тому
раз випало число очок, що не ділиться на 3 і після цього випало число очок кратне 3, тому  . Таблиця розподілу
. Таблиця розподілу


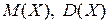 .
. .
.  . Якщо Х= 1, то
. Якщо Х= 1, то  . Якщо
. Якщо  . Якщо Х =3, то 6 очок випадали всі 3 рази і
. Якщо Х =3, то 6 очок випадали всі 3 рази і  . Знайдемо числові характеристики
. Знайдемо числові характеристики  значення
значення  , отримаємо
, отримаємо 
 з імовірностями
з імовірностями  . Обчислити
. Обчислити  .
.
 .
. 3)
3)  , де
, де  .
.









 ;
;

 ; 2)
; 2)  .
. ;
;  ;
;  .
. . Відповідь:
. Відповідь:  .
. .
. ;
;

 . Яка ймовірність, що
. Яка ймовірність, що  ?
? ;
;  .
.



