
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дисперсія випадкової величини. Середнє квадратичне відхиленняСодержание книги
Поиск на нашем сайте
Дисперсія випадкової величини або розподіл —це математичне сподівання, або математичне очікування піднесеного до другого степеня відхилення цієї змінної від її очікуваного значення (її математичного очікування). Отже дисперсія є вимірюванням величини розпорошеності значень цієї змінної, беручи до уваги всі її значення і їхні ймовірності або ваги. Наприклад, ідеальна шестистороння кістка, якщо кинути, має таке очікування
Її очікуване абсолютне відхилення таке
Але її очікуване квадратичне відхилення таке
Як ще один приклад, якщо монету підкинути двічі, кількість іверсів становить: 0 з імовірністю 0.25, 1 з імовірністю 0.5 і 2 з імовірністю 0.25. Отже очікування кількості аверсів таке:
і дисперсія така:
Означення Дисперсією випадкової величини Нехай випадкова змінна · Дисперсія дискретної випадкової величини
де
· Якщо випадкова величина
де
Твердження · Якщо є дискретна випадкова величина
Теореми · Дисперсія являє собою різницю математичного очікування
· Теорема Чебишова: Ймовірність будь-якої випадкової величини
· Закон додавання дисперсій: Дисперсія
Властивості · Дисперсія сталої величини дорівнює нулю, тобто · Додавання константи до значень випадкової величини не змінює дисперсії:
· Константу можна виносити в квадраті за знак дисперсії: · Дисперсія випадкової змінної є невід'ємною величиною, тобто Середнє квадратичне відхилення є важливою кількісною характеристикою в статистиці, теорії ймовірностей та оцінки точності вимірювань. Згідно з визначенням середнім квадратичним відхиленням називається корінь квадратний з дисперсії. Однак з цього визначення не зовсім зрозуміло - що характеризує ця величина і як порахувати значення дисперсії. 1. Нехай є кілька чисел, що характеризують будь-які однорідні величини. Наприклад, результати ізмерееній, зважувань, статистичних спостережень і т.п. Всі представлені величини повинні вимірюватися однієї і тієї ж одиницею виміру. Щоб знайти середнє квадратичне відхилення, виконайте такі дії. 2. Знайдіть відхилення кожного числа від його середнього значення: відніміть від кожного числа середнє арифметичне значення, порахували в попередньому пункті. 3. Визначте дисперсію (розкид) чисел: складіть квадрати знайдених відхилень і розділіть отриману суму на кількість чисел. 4. Витягніть з дисперсії квадратний корінь. Отримане число і буде середнім квадратичним відхиленням даної множини чисел. 5. Приклад. 6. Якщо є можливість скористатися програмою Excel, то обчислення дисперсії, а відповідно і середнього квадратичного відхилення можна істотно спростити.
49. Охарактеризувати початкові та центральні моменти.
|
||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 755; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.218.219 (0.01 с.) |






 називається математичне сподівання квадрата відхилення цієї величини від її математичного сподівання (середнього значення). Дисперсія є центральним моментом другого порядку. [1]
називається математичне сподівання квадрата відхилення цієї величини від її математичного сподівання (середнього значення). Дисперсія є центральним моментом другого порядку. [1] відповідно з ймовірностями
відповідно з ймовірностями  причому
причому  .
. ,
, і називається стандартним відхиленням величини
і називається стандартним відхиленням величини  ;
; — це оператор дисперсії випадкової величини.
— це оператор дисперсії випадкової величини. задана густиною імовірності, тоді дисперсія виглядає так:[2]
задана густиною імовірності, тоді дисперсія виглядає так:[2] ,
, , тобто це середнє значення величини
, тобто це середнє значення величини  ;
;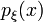 — функція густини імовірності.
— функція густини імовірності. , то дисперсія такої величини визначається так:[3]
, то дисперсія такої величини визначається так:[3] .
. квадрата випадкової величини і квадрата середнього значення
квадрата випадкової величини і квадрата середнього значення  .
.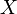 , яка приймає значення в границях
, яка приймає значення в границях 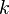 стандартних відхилень від середнього значення
стандартних відхилень від середнього значення  , тобто [4]
, тобто [4] .
. суми
суми  дискретних випадкових величин дорівнює алгебраїчній сумі
дискретних випадкових величин дорівнює алгебраїчній сумі  значень коваріаційної матриці системи цих величин:[5]
значень коваріаційної матриці системи цих величин:[5]
 , де
, де  .
. .
. .
. .
.


