
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Охарактеризувати скінченні множии та операціії над нимиСодержание книги
Поиск на нашем сайте
Охарактеризувати скінченні множии та операціії над ними Скінченна множина — множина, кількість елементів якої скінченна, тобто існує натуральне число k, що є числом елементів цієї множини. В інакшому випадку множина є нескінченною. Число елементів скінченної множини A завжди більша від числа елементів його власної підмножини B. Для множин можна ввести ряд операцій (теоретико-множинних операцій), результатом виконання яких будуть також множини. За допомогою цих операцій можна конструювати із заданих множин нові множини. а) Об’єднанням множин A і B (позначається A(B) називається множина тихелементів, які належать хоча б одній з множин A чи Bб) Перетином множин A і B (позначається A(B) називається множина, щоскладається з тих і тільки тих елементів, які належать множинам A і Bодночаснов). Різницею множин A і B (записується A\B) називається множина тихелементів, які належать множині A і не належать множині B.г). Симетричною різницею множин A і B (записується A(B, A(B або A(B)називається множина, що складається з усіх елементів множини A, які немістяться в B, а також усіх елементів множини B, які не містяться в A.Охарактиризувати предмет комбінаторики Комбінато́рика (Комбінаторний аналіз) — розділ математики, присвячений розв'язанню задач вибору та розташування елементів деякої, зазвичай скінченної, множини відповідно до заданих правил. Кожне таке правило визначає спосіб побудови деякої конструкції із елементів вихідної множини, що зветься комбінаторною конфігурацією. Тому на меті комбінаторного аналізу стоїть дослідження комбінаторних конфігурацій, алгоритмів їх побудови, оптимізація таких алгоритмів, а також розв'язання задач переліку. Найпростішими прикладами комбінаторних конфігурацій є перестановки, розміщення, комбінація та розбиття. Комбінаторика пов'язана з багатьма іншими розділами математики. Термін «комбінаторика» ввів Лейбніц, який у 1666 році опублікував свою працю «Міркування про комбінаторне мистецтво». Іноді під комбінаторикою розуміють більш широкий розділ дискретної математики, що включає теорію графів. Приклади комбінаторних конфігурацій і завдань Для формулювання і розв'язання комбінаторних задач використовують різні моделі комбінаторних конфігурацій. Прикладами комбінаторних конфігурацій є: Розміщенням з n елементів по k називається упорядкований набір з k різних елементів деякого n-елементного безлічі. Прикладами комбінаторних задач є: Скількома способами можна розмістити n предметів по m шухлядах так, щоб виконувалися задані обмеження? Відповідь: 52! (52 факторіал), тобто, 80658175170943878571660636856403766975289505440883277824000000000000 або приблизно 8,0658 × 1067. При грі в кістки кидаються дві кістки, і випали окуляри складаються; скільки існує комбінацій, таких, що сума очок на верхніх гранях дорівнює дванадцяти? Рішення: Кожен можливий результат відповідає функції F: \ {1, 2 \} \ to \ {1, 2, 3, 4, 5, 6 \} (аргумент функції - це номер кістки, значення - окуляри на верхній грані). Очевидно, що лише 6 +6 дає нам потрібний результат 12. Таким чином існує лише одна функція, яка ставить у відповідність 1 число 6, і 2 число 6. Або, іншими словами, існує всього одна комбінація, така, що сума очок на верхніх гранях дорівнює дванадцяти. Розділи комбінаторики Перечислительного комбінаторика (або обчислюється комбінаторика) розглядає задачі про перерахування або підрахунку кількості різних конфігурацій (наприклад, перестановок) утворюваних елементами кінцевих множин, на які можуть накладатися певні обмеження, такі як: розрізнюваність або нерозрізненість елементів, можливість повторення однакових елементів і т. п. Кількість конфігурацій, утворених декількома маніпуляціями над безліччю, підраховується згідно з правилами додавання і множення. Типовим прикладом завдань даного розділу є підрахунок кількості перестановок. Інший приклад - відома Задача про листи. До даного розділу належать деякі питання теорії графів, а також теорії матроідов. Прикладом цього розділу може служити наступна задача: яка найбільша розмірність графа, який задовольняє певним властивостям. Теорія Рамсея вивчає наявність регулярних структур у випадкових конфігураціях елементів. Прикладом твердження з теорії Рамсея може служити наступне: в групі з 6 чоловік завжди можна знайти трьох чоловік, які або попарно знайомі один з одним, або попарно незнайомі. У термінах структурної комбінаторики це ж твердження формулюється так: в будь-якому графі з 6 вершинами знайдеться або кліка, або незалежна безліч розміру 3. Імовірнісна комбінаторика Цей розділ відповідає на питання виду: яка вірогідність присутності певного властивості у заданої множини. Топологічна комбінаторика (англ.) застосовує ідеї та методи комбінаторики в топології, при вивченні дерева прийняття рішень, частково впорядкованих множин, розмальовок графа і ін Інфінітарная комбінаторика (англ.) - застосування ідей та методів комбінаторики до нескінченних (в тому числі, незліченною) множинам. Охаректиризувати основні принципи комбінаторики Двома основними правилами комбінаторики є: Перестановки Нехай треба підрахувати число способів, за якими можна розмістити в ряд n предметів. Якщо дані предмети розглядати як елементи множини то кожне розміщення є скінченною множиною, елементи якої записано у певному порядку. Скінченні множини, для яких істотним є порядок елементів, називаються впорядкованими. Вказати порядок розміщення елементів у скінченній множині з п елементів означає поставити у відповідність кожному елементу даної множини певне натуральне число від 1 до п. Дві впорядковані множини називаються рівними, якщо вони складаються з тих самих елементів і однаково впорядковані. З цього випливає, що множини (а, b, с) і (b, с, а) - це різні впорядковані множини. Означення. Будь-яка впорядкована множина, що складається з п елементів, називається перестановкою з п елементів. Перестановки з п елементів складаються з одних і тих самих елементів, а відрізняються одна від одної лише порядком.
Розміщення Нехай деяка множина складається з п різних елементів. Означення. Розміщеннями з п елементів по k називаються підмножини, що мають k елементів, вибраних з даних п елементів і розміщених у певному порядку (k<п). Розміщення можуть відрізнятися одне від одного або самими елементами, або порядком їх розміщення.
Сполучення
Запис впорядкованих множин Впорядковані (скінченні або такі, елементи яких можна перерахувати) множини часто записують, розташовуючи їх елементи в заданому порядку в круглих дужках. Наприклад, записи (1; 2; 3) і (2; 1; 3) (1) представляють різні скінченні впорядковані множини, які можна отримати з однієї і тієї ж множини {1; 2; 3}, впорядковуючи її двома різними способами. Для запису скінченної впорядкованої множини у виді, аналогічному (1), необхідно вказати перший елемент впорядкованої множини і вказати порядок (правило) розташування наступних елементів. Шукаємо за формулою Приклад Припустимо, що монету підкидають один раз. Простір елементарних подій, цього експерименту має вигляд Ω = {Г, Р}, де Г означає появу герба, буква Р — появу решки. Монету підкидають двічі. Простором елементарних подій цього експерименту є множина Ω = {ГГ, ГР, РГ, РР}. Тут ГР означає, наприклад, що при першому підкиданні з'явився герб, а при другому — решка. Підкидають шестигранний гральний кубик на якому вибиті очки від 1 до 6. Нас цікавить число очок, яке випало. Простором елементарних подій тут може бути Ω = {1,2,3,4,5,6}. Зауваження Формула повної ймовірності також має наступну інтерпретацію. Нехай
Тоді
тобто апріорна ймовірність події рівна середньому його апостеріорної ймовірності. Наслідок Важливим наслідком формули Баєса є формула повної ймовірності події, що залежить від декількох несуміснних гіпотез (і тільки від них).
Властивості Нехай p — ймовірність успіху в схемі Бернуллі, q=1-p.Тоді найімовірнішою серед подій
18 охарактеризувати формулу Пуасона Формула Пуассона дає приблизне значення імовірності
Значить Теорема Якщо
Гранична форма теореми стверджує, що
для Можливо, формулювання стає ясним не відразу, проте практичний зміст теореми простий: при великих значеннях n імовірність спостерігаючи рівно m успіхів можна приблизно розраховувати за формулою: Властивості Випадкова величина X — це вимірна функція, визначена на даному вимірному просторі
Нехай x 1, x 2, … — значення випадкової величини X. Одне і те саме значення x j може відповідати, взагалі кажучи, різним елементарним подіям. Множина усіх цих елементарних подій утворює складену випадкову подію, що полягає в тому, що X = x j. Ймовірність цієї події позначається
визначає розподіл ймовірностей (слід відрізняти від функції розподілу ймовірностей) випадкової величини X. Очевидно, що:
Якщо дві або більше випадкових величини X 1, X 2, …, X n визначено на одному просторі елементарних подій, то їх спільний розподіл задається системою рівнянь, в яких всім комбінаціям Випадкові величини називаються незалежними, якщо для довільної комбінації значень
Тобто, якщо X k залежить лише від k -го випробування, то випадкові величини X 1, X 2, …, X n взаємно незалежні. Ймовірність випадкової величини · Ймовірність випадкової величини
де
Функція розподілу ймовірностей — В теорії ймовірностей це функція, яка повністю описує розподіл ймовірностей випадкової величини. Нехай
називається функцією розподілу ймовірностей або кумулятивною функцією розподілу ймовірностей випадкової величини ξ. Вираз в правій частині рівності є ймовірністю того, що випадкова величина Функція розподілу ймовірностей — В теорії ймовірностей це функція, яка повністю описує розподіл ймовірностей випадкової величини. Нехай
називається функцією розподілу ймовірностей або кумулятивною функцією розподілу ймовірностей випадкової величини ξ. Вираз в правій частині рівності є ймовірністю того, що випадкова величина 21 охарактеризувати основні закони розподілу дискретних випадкових величин Законом розподілу дискретної випадкової величини на- зивають відповідність між можливими значеннями і їх імовірностями. Його задають таблично, графічно чи аналітич-но (у виді формул). Сума імовірностей закону розподілу дорівнює 1: ^pi=l або ^ pi = 1, якщо множина можливих значень дискретної випадкової величини зліченна. Дві випадкові величини називаються незалежними, якщо закон розподілу однієї з них не залежить від того, які можливі значення прийняла друга величина. В протилежному випадкувипадкові величини є залежними. Декілька випадкових вели-чин називаються взаємно незалежними, якщо закони розпо-ділу будь-якого числа з них не залежать від того, які можливі значення набула решта величин. Добутком незалежних випадкових величин Х та Y нази-вають випадкову величину ХY, можливі значення якої рівні всеможливим добуткам співмножників Х і Y. Імовірності цих добутків рівні добуткам імовірностей відповідних співмнож-ників. Якщо деякі добутки ХіГі рівні між собою, то імовірність цього добутку рівна сумі імовірностей цих добутків. Сумою випадкових величин Х і Y називають випадкову величину Х + Y, можливі значення якої рівні всеможливим су-мам з доданків Х та Y. Імовірності цих сум рівні добуткам імовірностей доданків; для залежних величин - добуткам імо-вірностей одного доданку на умовну імовірність другого, якщо деякі суми рівні між собою, то імовірність такої суми рівна сумі відповідних імовірностей доданків. Математичним сподіванням дискретної випадкової величини називають суму добутків всіх її можливих значень на їх імовірності: M(X) = xlpl +х2р2 +... + хпрп =^jxipi (4.1.1). Якщо дискретна випадкова величина Х приймає зліченну множину можливих значень, то М(Х) = /^ xtpt при умові, що ряд збігається абсолютно. Математичне сподівання при-близно рівне середньому арифметичному спостережних зна- чень випадкової величини: М(Х) «X. Властивості математичного сподівання: 1. Математичне сподівання сталої величини є сама ця стала: М{С) = С. Сталий множник можна виносити за знак математич-ного сподівання: М(СХ) = СМ(Х).3. Математичне сподівання добутку двох незалежних випадкових величин дорівнює добутку їх математичних сподівань: M(XY) = M{X)M{Y). Наслідок. Математичне сподівання добутку декількох взаємно незалежних випадкових величин дорівнює добутку їх математичних сподівань 4. Математичне сподівання суми двох випадкових величин дорівнює сумі їх математичних сподівань: М(Х + Y) =M(X) + M(Y). Наслідок 2. Математичне сподівання різниці двох випадкових величин дорівнює різниці їх математичних сподіваньДисперсією D(X) випадкової величини Х називають мате-матичне сподівання квадрата відхилення цієї величини від її математичного сподівання М(Х): D{X) =М[Х-М(Х)]2 (4.1.2). Дисперсія має розмірність квадратних одиниць вимірю-ваної величини. Щоб отримати розмірність міри розсіювання в одиницях вимірюваної величини розглядають квадратний корінь з дисперсії сг(Х) = -JD(X) (4.1.4), який називають середнім квадратичним відхиленням, або стандартом. Властивості дисперсії: 1. Дисперсія будь-якої випадкової величини невід’ємна: D(X) > 0.Наслідок. Для будь-якої випадкової величини (M(X))2 <M(X2). 2. Дисперсія сталої дорівнює нулю: D(C) = 0. 3. Сталий множник можна винести за знак дисперсії, під-нісши його до квадрату: D(CX) = C2D(X). 4. Дисперсія суми двох незалежних випадкових величин дорівнює сумі їх дисперсій: D(X + Y) = D(X) + D(Y). Наслідок 1. Дисперсія суми попарно незалежних випад-кових величин ХиХ2,... Хn незалежних у сукупності, дорівнює сумі їх дисперсій: D{XX + X2 +... + Xn) = D{XX) + D(X2) +... + + D(Xn). Наслідок 2. Дисперсія суми постійної величини і випад-кової дорівнює дисперсії випадкової величини: D(C + X) = = D(X). 5. Дисперсія різниці двох незалежних випадкових вели- чин дорівнює сумі їх дисперсій: D(X - Y) = D(X) + D(Y). Теорема. Середнє квадратичне відхилення суми скінчен-ного числа взаємно незалежних випадкових величин дорівнює квадратному кореню з суми квадратів середніх квадратичних відхилень цих величин: сг(X1+X2+... + Xn) = л/сг2(X1) + сг2(X2) +... + сг2(Xn) (4.1.5). Якщо декілька випадкових величин мають однакові розподіли, то їх числові характеристики (математичне сподівання, дисперсія, і т. д.) однакові. Способи задання Нехай ξ — абсолютно неперервна випадкова величина, тоді є два способа її задання: · за допомогою функції густини імовірності · за допомогою функції розподілу ймовірностей · функція розподілу · функція щільності Щільність ймовірності Нехай Визначення 1. Ймовірність
Якщо ймовірність
де використано загальноприйняте скорочення Визначення 2. У більш загальному вигляді, нехай
то таку функцію називають щільністю заходи ν по мірі μ, Або похідної Радону-Никодима заходи ν щодо міри μ, І позначають
Визначення Кажуть, що випадкова величина має неперервний рівномірний розподіл на відрізку
Пишуть: Функція розподілу Інтегруючи визначену вище щільність отримуємо:
Оскільки щільність рівномірного розподілу розривна в граничних точках відрізка
Функція моментів Простим інтегруванням отримуємо:
звідки знаходимо всі потрібні моменти неперервного рівномірного розподілу:
Таким чином
Сутність кореляції Кореляція (від лат. correlatio - співвідношення) - це статистична залежність між випадковими величинами, що носить імовірнісний характер. Кореляційні зв'язки можна вивчати на якісному рівні з діаграм розсіяння емпіричних значень змінних X і Y (рис. 2.51) і відповідним чином їх інтерпретувати. Так, наприклад, якщо підвищення рівня однієї змінною супроводжується підвищенням рівня іншої, то йдеться про позитивну кореляцію або прямий зв'язок (рис. 2.51 а, б). Якщо ж зростання однієї змінної супроводжується зниженням значень іншої, то маємо справу з негативною кореляцією або зворотним зв'язком (рис. 2.51 г, ґ). Нульовою називається кореляція за відсутності зв'язку змінних (рис. 2.51 в). Проте нульова загальна кореляція може свідчити лише про відсутність лінійної залежності, а не взагалі про відсутність будь якого статистичного зв'язку Коефіцієнт кореляції Нехай
де:
41. Охарактеризувати геометричну ймовірність Геометрична ймовірність – це поняття ймовірності,що запроваджується так: Нехай Це пов'язане з інтерпретацією ймовірності як міри на обраному просторі елементарних подій. В даному випадку він збігається з eвклідовим простором. Формально Стохастичний експеримент полягає в обранні навмання точки з множини
де Так визначену ймовірність назвемо геометричною (зрозуміло, що множина 42. Охарактеризувати незалежність подій У теорії ймовірностей дві випадкові події називаються незалежними, якщо настання однієї з них не змінює вірогідність настання іншої. Аналогічно, дві випадкові величини називають незалежними якщо значення однієї з них не впливає на розподіл значень іншої. Незалежні події Вважатимемо, що дано фіксований ймовірнісний простір Означення 1. Дві події
Зауваження 1. В тому випадку, якщо ймовірність однієї події, скажемо
тобто умовна ймовірність події Означення 2. Нехай є сімейство (скінченне або нескінченне) випадкових подій
Означення 3. Нехай є сімейство (скінчене або нескінчене) випадкових подій
Приклад 1. Монета кидається двічі. Ймовірність появи герба в першому випробуванні не залежить від появи чи непояви герба в другому випробуванні. В свою чергу, ймовірність появи герба в другому випробуванні не залежить від результатів першого випробування. Отже, події А — «поява герба в першому випробуванні» і В — «поява герба в другому випробуванні» — незалежні. 43 Охарактеризувати теорему множення ймовірностей. Добутком двох подій А і В називається подія С, що полягає у здійсненні під час одиничного випробовування й події А, і події В. Подія А називається від події В, якщо ймовірність події А не залежить від того, відбулась чи ні подія В. Дві події А та В називають залежними, якщо ймовірність настання однієї з них залежить від того, настала друга подія чи ні. Умовною ймовірністю РА(В) події В називається ймовірність події В, знайдена в припущенні, що подія А вже настала. З означення назалежних подій випливає, що настання однієї з них не змінює ймовірності настання другої. Тому для незалежних подій справджуються рівності:
Отже, умовні ймовірності незалежних подій дорівнюють їх безумовним імовірностям. Теорема 1. Імовірність добутку двох залежних подій А і В дорівнює добутку ймовірності однієї з них на умовну ймовірність другої, яка знайдена з припущенням того, що перша подія настала, тобто
Доведення. Нехай з усієї кількості n елементарних подій k сприяють події А і нехай з цих подій l сприяють події В, а, отже і події АВ. Тоді:
що й треба було довести. Теорема 2. Імовірність добутку двох незалежних подій А і В дорівнює добутку імовірностей цих подій, тобто
Доведення. Якщо А і В - незалежні події, то
і формула
перетворюється в формулу
44. Охарактеризувати формулу Бернуллі та алгоритм розв’язування задач за допомогою неї. У теорії ймовірності, формула Бернуллі дозволяє обчислити ймовірність успіхів у серії незалежних експериментів. Якщо ймовірність
Умови використання Якщо відбувається де
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 358; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.30.113 (0.015 с.) |

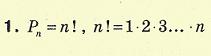
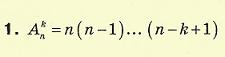
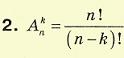
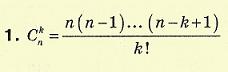
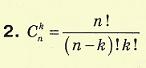
 - випадкова величина, що має розподіл
- випадкова величина, що має розподіл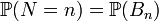 .
.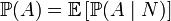 ,
,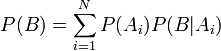 — ймовірність настання події B, що залежить від гіпотез
— ймовірність настання події B, що залежить від гіпотез 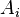 , якщо відомі їх ступені достовірності
, якщо відомі їх ступені достовірності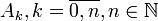 є подія
є подія  , де
, де 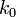 можна знайти з нерівності
можна знайти з нерівності 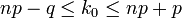 .
.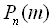 в тому випадку, коли число випробувань n велике, а імовірність p=P(А) в кожному з окремих випробувань маленька, оскільки добуток цих чисел
в тому випадку, коли число випробувань n велике, а імовірність p=P(А) в кожному з окремих випробувань маленька, оскільки добуток цих чисел 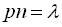 є заданим числом, незалежним від n, а значить
є заданим числом, незалежним від n, а значить 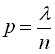 , досить мале. Тоді
, досить мале. Тоді  , m =0, 1, 2,…, n. Сума всіх ймовірностей дорівнює:
, m =0, 1, 2,…, n. Сума всіх ймовірностей дорівнює:
 де
де  . Одержано формулу Пуассона або закон Пуассона. Цей закон дає можливість наближати біноміальний розподіл при великій кількості випробувань і малій імовірності події А в кожному випробуванні.
. Одержано формулу Пуассона або закон Пуассона. Цей закон дає можливість наближати біноміальний розподіл при великій кількості випробувань і малій імовірності події А в кожному випробуванні. , тоді для k в
, тоді для k в  -околі точки np, існує наближення[1]
-околі точки np, існує наближення[1]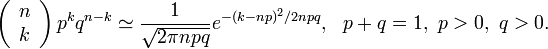



 , тобто, вона визначається шляхом зіставлення кожної елементарної події з деякимдійсним числом. Більш формально:
, тобто, вона визначається шляхом зіставлення кожної елементарної події з деякимдійсним числом. Більш формально: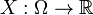 називається випадковою величиною, якщо
називається випадковою величиною, якщо  , де
, де  --
-- 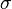 -алгебра Борелевих множин на
-алгебра Борелевих множин на  .
.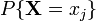 . Система рівнянь:
. Система рівнянь:
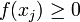 та
та 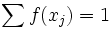 .
. ,
, 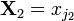 і т. д. призначаються визначені ймовірності.
і т. д. призначаються визначені ймовірності.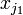 ,
,  , …,
, …, 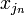 виконується рівність:
виконується рівність: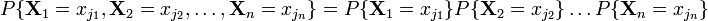
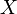 дорівнює інтегралу ймовірностей взятому по її області значень: [4]
дорівнює інтегралу ймовірностей взятому по її області значень: [4]
 ;
; 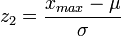 — граничні значення нормованої величини
— граничні значення нормованої величини 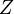 ;
; — це середнє значення величини
— це середнє значення величини 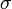 — cтандартне відхилення цієї величини.
— cтандартне відхилення цієї величини. — ймовірнісний простір, в якому
— ймовірнісний простір, в якому 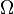 — множина елементарних подій,
— множина елементарних подій, 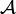 — сукупність підмножин
— сукупність підмножин 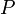 — міра на
— міра на 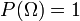 . Функція
. Функція 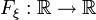 , визначена
, визначена 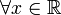 рівністю
рівністю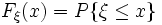 ,
,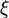 набуває значень менших або рівних
набуває значень менших або рівних  .
.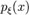 ;
;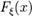 .
.

 є ймовірнісної мірою на
є ймовірнісної мірою на 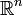 , Тобто визначено ймовірнісна простір
, Тобто визначено ймовірнісна простір  , Де
, Де 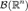 позначає борелевскую σ-алгебру на
позначає борелевскую σ-алгебру на 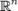 . Нехай m позначає міру Лебега на
. Нехай m позначає міру Лебега на  ), Якщо будь борелевское безліч нульової міри Лебега також має ймовірність нуль:
), Якщо будь борелевское безліч нульової міри Лебега також має ймовірність нуль: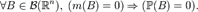
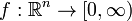 така, що
така, що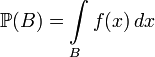 ,
,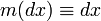 , І інтеграл розуміється в сенсі Лебега.
, І інтеграл розуміється в сенсі Лебега.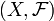 - Довільне вимірне простір, а μ і ν - Дві заходи на цьому просторі. Якщо знайдеться неотрицательна f, Що дозволяє висловити міру ν через міру μ у вигляді
- Довільне вимірне простір, а μ і ν - Дві заходи на цьому просторі. Якщо знайдеться неотрицательна f, Що дозволяє висловити міру ν через міру μ у вигляді .
.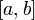 ,де
,де 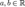 , якщо щільність
, якщо щільність  має вигляд:
має вигляд: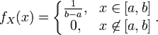
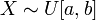 . Деколи значення щільності в граничних точках
. Деколи значення щільності в граничних точках  і
і 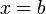 міняють на інші, наприклад
міняють на інші, наприклад  .Так як інтеграл Лебега від щільності не залежить від поведінки останньої на множинах міри нуль, ці варіації не впливають на знаходження зв'язаних з цим розподілом імовірностей.
.Так як інтеграл Лебега від щільності не залежить від поведінки останньої на множинах міри нуль, ці варіації не впливають на знаходження зв'язаних з цим розподілом імовірностей.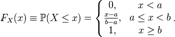
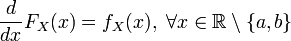 .
.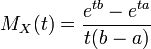 ,
,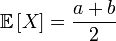 ,
,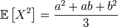 ,
,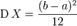 .
.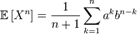 .
.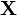 та
та 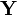 — випадкові величини з математичним сподіванням μ X та μ Y. Їх коефіцієнт кореляції позначається як
— випадкові величини з математичним сподіванням μ X та μ Y. Їх коефіцієнт кореляції позначається як 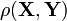 і дорівнює:[1]
і дорівнює:[1]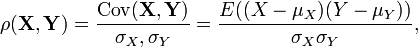
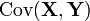 — коваріація величин
— коваріація величин  — стандартне відхилення величин
— стандартне відхилення величин 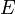 — оператор математичного сподівання.
— оператор математичного сподівання. - підмножина
- підмножина 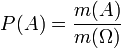 де
де 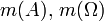 - довжина, площа чи об’єм множин
- довжина, площа чи об’єм множин 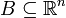 . За його математичну модель прийнято розглядати ймовірнісний простір
. За його математичну модель прийнято розглядати ймовірнісний простір 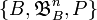 , де
, де 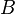 - борелева множина з
- борелева множина з  ,
, 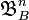 - клас борелевих підмножин множини
- клас борелевих підмножин множини 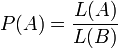 ,
,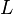 - міра Лебега на
- міра Лебега на 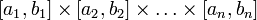 , дорівнює
, дорівнює 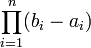 ).
). .
. .
.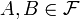 називають незалежними, якщо
називають незалежними, якщо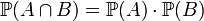 .
.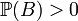 , визначення незалежності еквівалентне:
, визначення незалежності еквівалентне: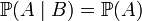 ,
,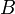 дорівнює безумовній вірогідності події
дорівнює безумовній вірогідності події 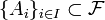 , де
, де 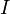 — довільна індексна безліч. Тоді ці події є попарно незалежними, якщо будь-які дві події з цього сімейства незалежні, тобто
— довільна індексна безліч. Тоді ці події є попарно незалежними, якщо будь-які дві події з цього сімейства незалежні, тобто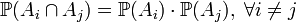 .
.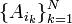 вірно:
вірно: .
.


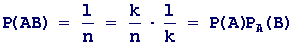

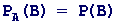
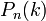 того, що подія
того, що подія 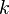 разів в
разів в 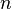 незалежних випробуваннях дорівнює
незалежних випробуваннях дорівнює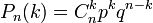 або
або



