
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Охарактеризувати ряд і перетворення Фур’є.Содержание книги
Поиск на нашем сайте
Ряд Фур'є — в математиці — спосіб представлення довільної складної функції сумою простіших. В загальному випадку кількість таких функцій може бути нескінченною, при цьому чим більше таких функцій враховується при розрахунку, тим вищою стає кінцева точність представлення даної функції. В більшості випадків в якості найпростіших використовуються тригонометричні функції синуса і косинуса. В цьому випадку ряд Фур'є називається тригонометричним, а обчислення такого ряду часто називають розкладом на гармоніки. Ряди названі на честь французького математика Жана Батиста Жозефа Фур'є. Перетворення Фур'є — інтегральне перетворення однієї комплекснозначної функції дійсної змінної на іншу. Тісно пов'язане з перетворенням Лапласа та аналогічне розкладу у ряд Фур'є для неперіодичних функцій. Це перетворення розкладає дану функцію на осциляторні функції. Використовується для того, щоби розрахувати спектр частот для сигналів змінних у часі (таких як мова або електрична напруга). Перетворення названо на честь французького математика Жана Батиста Жозефа Фур'є, який ввів поняття в 1822 році. Визначення Перетворення Фур'є функції
Обернене перетворення Фур'є задається виразом
Властивості Якщо задані інтегровні функції Лінійність Для довільних комплексних чисел a та b, якщо h (x) = aƒ (x) + bg (x), тоді Трансляція Для довільного дійсного числа x 0, якщо h (x) = ƒ (x − x 0), тоді Модуляція Для довільного дійсного числа ξ 0, якщо h (x) = e 2 πixξ 0 ƒ (x), тоді Масштабування Для не рівного нулю дійсного числа a, якщо h (x) = ƒ (ax), тоді Спряження Якщо Зокрема, якщо ƒ дійсне, тоді має місце "умова дійсності" Згортка Якщо Використання Перетворення Фур'є застосовуються для отримання частотного спектру неперіодичної функції, наприклад, електричного сигналу, тобто для представлення сигналу у вигляді суми гармонічних коливань. При цьому використовується властивість згортки.
На практиці, це можна побачити у використанні системами розподіленого обчислення для пошуку можливих сигналів позаземних цивілізацій (проекти SETI і відповідно SETI@Home). Нехай відгук системи на збурення у вигляді сигналу
де Застосовуючи перетворення Фур'є до обох частин рівняння, отримуємо
Оскільки
де
де
Важливим висновком з цього перетворення є те, що вихідний спектр отримується з вхідного простим множенням на функцію відклику системи Охарактеризувати математичне сподівання. Перейти до: навігація, пошук Математи́чне сподіва́ння, середнє значення — одна з основних числових характеристик кожної числової змінної. Воно є узагальненим поняттям середнього значення сукупності чисел на той випадок, коли елементи множини значень цієї сукупності мають різну "вагу", ціну, важливість, пріоритет, що є характерним для значень випадкової змінної. [1] Оскільки, випадкова величина може бути дискретною або задана густиною розподілу ймовірностей, тому теорія ймовірностей наводить два означення математичного сподівання. Нехай дискретна випадкова змінна · Означення Чебишова: Математичним сподіванням будь-якої величини називається сума всіх можливих для неї значень, помножених на ймовірності їх: [2]
де
Твердження · Якщо є випадкова величина
Означення 2 Нехай випадкова змінна · Математичним сподіванням такої числової змінної
Сподівання існує, якщо цей інтеграл абсолютно збіжний. 47 Охарактеризувати моменти випадкової величини. Моментом n-того порядку випадкової величини Величина Перший момент є математичним сподіванням Якщо дана випадкова величина
якщо математичне сподівання в правій частині цієї рівності визначене. Початковим моментом k-го порядку називається величина:
якщо математичне сподівання в правій частині цієї рівності визначене.
якщо математичне сподівання в правій частині цієї рівності визначене.
|
||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 259; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.157.7 (0.01 с.) |

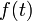 математично визначається як комплексна функція
математично визначається як комплексна функція  , яка задається інтегралом[1]
, яка задається інтегралом[1]

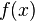 ,
,  та
та  та їхні відповідні перетворення Фур'є
та їхні відповідні перетворення Фур'є  ,
,  та
та  , тоді самому перетворенню властиво наступне:
, тоді самому перетворенню властиво наступне:

 .
. . Випадок a = −1 призводить до властивості "обернення часу", згідно з якою: якщо h (x) = ƒ (− x), тоді
. Випадок a = −1 призводить до властивості "обернення часу", згідно з якою: якщо h (x) = ƒ (− x), тоді  .
. , тоді
, тоді 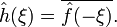

 , тоді
, тоді 
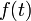 має вигляд
має вигляд ,
, — певна функція. Такий запис означає, що відгук системи залежить не тільки від моментального значення збурення, а також від того збурення, яке було певний час тому, і, яке, змінило стан системи.
— певна функція. Такий запис означає, що відгук системи залежить не тільки від моментального значення збурення, а також від того збурення, яке було певний час тому, і, яке, змінило стан системи.
 ,
, — дельта-функція Дірака, інтегрування дає
— дельта-функція Дірака, інтегрування дає ,
, .
. .
. може набувати значення
може набувати значення  відповідно з ймовірностями
відповідно з ймовірностями  причому
причому  .
.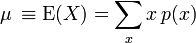 ,
, — це середнє значення випадкової величини
— це середнє значення випадкової величини  ;
;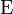 — оператор математичного сподівання;
— оператор математичного сподівання; — математичне сподівання величини
— математичне сподівання величини 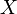 , сума ймовірностей значень якої менше одиниці, тобто
, сума ймовірностей значень якої менше одиниці, тобто  , то середнє значення такої величини визначається так: [3]
, то середнє значення такої величини визначається так: [3]
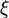 задана густиною розподілу ймовірностей:
задана густиною розподілу ймовірностей: 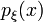 ,
, 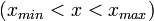 .
. .
. , якщо
, якщо  .
. називається абсолютним моментом випадкової величини
називається абсолютним моментом випадкової величини  визначена на деякому імовірнісному просторі, то центра́льним моментом (k -го порядку) випадкової величини
визначена на деякому імовірнісному просторі, то центра́льним моментом (k -го порядку) випадкової величини 

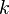 -им факторіальним моментом випадкової величини
-им факторіальним моментом випадкової величини 



