
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Початкові і центральні теоретичні моментиСодержание книги
Поиск на нашем сайте
Розглянемо д. в.в. Знайдемо математичне сподівання: М Закон розподілу
Бачимо, що М Якби Тому важливо розглядати математичне сподівання цілого додатного степеня випадкової величини (не тільки дискретної, але й неперервної). Взагалі, початковий момент (starting point) порядку k випадкової величини
Для дискретної випадкової величини: Для неперервної випадкової величини: так Користуючись цими моментами, формулу для обчислення дисперсії можна записати Крім моментів в. в. Центральним моментом порядку k в. в. Легко одержуються співвідношення, які з’єднують початкові і центральні моменти:
Використовуючи означення центрального моменту та властивості математичного сподівання, отримаємо формулу:
Третій центральний момент 50. Охарактеризувати неперервні розподіли Рівномірний розподіл (неперервний) — в теорії імовірностей розподіл, який характеризується тим, що ймовірність будь-якого інтервала залежить тільки від його довжини. Кажуть, що випадкова величина має неперервний рівномірний розподіл на відрізку
Пишуть: 51. Охарактеризувати систему двох випадкових величин. ипадкові величини, можливі значення яких визначають-ся двома, трьома,... n числами називаються відповідно двомірними, трьохмірними,... n-мірними. Двомірна випад-кова величина (X, Y) визначається двома складовими або компонентами Х і Y, що утворюють систему двох випадкових величин. Геометрична інтерпретація двомірної величини – випад-кова точка М(Х; Y) на площині ХОY або як випадковий вектор ОМ. Якщо складові Х і Y – дискретні, то двомірна величина є дискретною, якщо складові неперервні, то – неперервною. Законом розподілу імовірностей двомірної дискретної ви-падкової величини називають відповідність пар чисел (xi,yj) і їх імовірностей p(xi, y j) (і = 1, 2,...., n; j = 1, 2,..., m). Закон розподілу задають у вигляді: а) аналітично; б) таблиці з по-двійним входом (табл. 4.13.1). Охарактеризувати центральну граничну теорему Центральна гранична теорема — теорема теорії ймовірностей про збіжність розподілу суми незалежних однаково розподілених випадкових величин до нормального розподілу. Ця теорема підкреслює особливість нормального розподілу в теорії ймовірностей. Центральна гранична теорема для незалежних послiдовностей Формулювання Ліндеберга Нехай
Де Формулювання Ляпунова Теорема названа на честь російського математика Олександра Ляпунова. У цьому варіанті центральної граничної теореми випадкові величини ЦГТ Ляпунова[3]: Нехай { Xi } — послідовність незалежних випадковех величин, таких, що кожна з них має скінченне математичне сподівання
Тоді сума
На практиці зазвичай найлегше перевірити умову Ляпунова для Формулювання Лінденберга Докладніше: Умова Лінденберга Використовуючи ті позначення що й у попередньому параграфі, замінюючи умову Ляпунова на слабшу (запропоновану фінським математиком Ліндебергом у 1920 році) можна отримати нове формулювання центральної граничної теореми. Якщо для кожного
де 53. Охарактеризувати закон великих чисел. Закон великих чисел в теорії імовірностей стверджує, що емпіричне середнє (арифметичне сeреднє) скінченної вибірки із фіксованого розподілу близьке до теоретичного середнього (математичного сподівання) цього розподілу. В залежності від виду збіжності розрізняють слабкий закон великих чисел, коли має місце збіжність за ймовірністю, і посилений закон великих чисел, коли має місце збіжність майже скрізь. Завжди знайдеться така кількість випробувань, при якій з будь-якою заданою наперед імовірністю частота появ деякої події буде як завгодно мало відрізнятися від її імовірності. Форми ЗВЧ Нижче описано дві версії ЗВЧ: Слабкий закон великих чисел та Посилений закон великих чисел. Обидва закони стверджують, що з певною достовірністю середнє вибірки
прямує до математичного сподівання
де X 1, X 2,... — скінченна послідовність н.о.р. випадкові величини зі скінченним математичним сподіванням E(X 1) = E(X 2) =... = µ < ∞.
Слабкий закон великих чисел Нехай є нескінченна послідовність однаково розподілених і некорельованих випадкових величин
Тоді
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 229; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.243.86 (0.006 с.) |

 , задану законом розподілу:
, задану законом розподілу: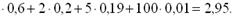
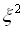
 .
.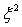 значно більше М
значно більше М 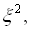 яке відповідає значенню х =100 величини
яке відповідає значенню х =100 величини 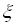 , стало рівним 10000, тобто значно збільшилося; імовірність цього значення залишилась. Таким чином, перехід від М
, стало рівним 10000, тобто значно збільшилося; імовірність цього значення залишилась. Таким чином, перехід від М 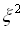 ,а тим більше
,а тим більше  ,
,  , дав можливість ще більше «врахувати вклад» цих великих, але малоймовірних значень.
, дав можливість ще більше «врахувати вклад» цих великих, але малоймовірних значень.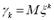 .
.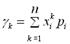 .
.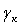 =
=  ,
,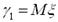 ,
, 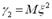 .
.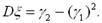
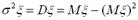 розглядаються моменти відхилення
розглядаються моменти відхилення  .
.
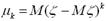 Значить,
Значить, 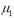 = М
= М  =0,
=0, 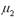 = М
= М 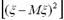 =
= 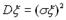 .
.
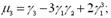

 дає характеристику асиметрії (скошеності) розподілу (рис. 2.6, а; б). Якщо випадкова величина
дає характеристику асиметрії (скошеності) розподілу (рис. 2.6, а; б). Якщо випадкова величина  ,де
,де 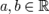 , якщо щільність
, якщо щільність  має вигляд:
має вигляд:
 . Деколи значення щільності в граничних точках
. Деколи значення щільності в граничних точках  і
і 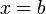 міняють на інші, наприклад
міняють на інші, наприклад  .Так як інтеграл Лебега від щільності не залежить від поведінки останньої на множинах міри нуль, ці варіації не впливають на знаходження зв'язаних з цим розподілом імовірностей.
.Так як інтеграл Лебега від щільності не залежить від поведінки останньої на множинах міри нуль, ці варіації не впливають на знаходження зв'язаних з цим розподілом імовірностей. — послідовність взаємно незалежних випадкових величин з однаковими розподілами. Припустімо, що
— послідовність взаємно незалежних випадкових величин з однаковими розподілами. Припустімо, що  та
та 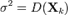 існують. Нехай
існують. Нехай  . Тоді для довільних фіксованих
. Тоді для довільних фіксованих 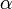 ,
, 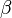 (
( ):
):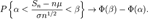
 — нормальна функція розподілу.[1][2]
— нормальна функція розподілу.[1][2]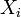 мають бути незалежними, але не обов'язково однаково розподіленими. Теорема також вимагає щоб випадкові виличини
мають бути незалежними, але не обов'язково однаково розподіленими. Теорема також вимагає щоб випадкові виличини  мали скінченні моменти деякого порядку (2 + δ) і швидкість зростання цих моментів має бути обмежена умовою Ляпунова.
мали скінченні моменти деякого порядку (2 + δ) і швидкість зростання цих моментів має бути обмежена умовою Ляпунова.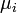 і дисперсію
і дисперсію 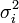 . Позначимо
. Позначимо 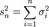 . Якщо для деякого
. Якщо для деякого 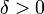 виконується умова Ляпунова
виконується умова Ляпунова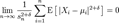
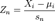 прямує за розподілом до стандартного нормального розподілу, при
прямує за розподілом до стандартного нормального розподілу, при 
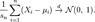
 . Якщо послідовність випадкових величин задовольняє умову Ляпунова, то вона задовольняє також умову Лінденберга. Зворотне твердження не правильне.
. Якщо послідовність випадкових величин задовольняє умову Ляпунова, то вона задовольняє також умову Лінденберга. Зворотне твердження не правильне.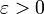 виконуэться
виконуэться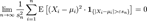
 — характеристична функція. Тоді розподіл стандартизованої суми Zn прямує до стандартного нормального розподілу N(0,1).
— характеристична функція. Тоді розподіл стандартизованої суми Zn прямує до стандартного нормального розподілу N(0,1).

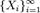 , визначених на одному імовірносному просторі
, визначених на одному імовірносному просторі  . Їх коваріація
. Їх коваріація  . Нехай
. Нехай 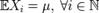 . Позначимо
. Позначимо 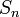 вибіркове середнє перших
вибіркове середнє перших  членів:
членів: .
.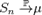 .
.


