
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема додавання сумісних подійСодержание книги
Поиск на нашем сайте
Сумою 2-х сумісних подій називають подію, що складається з появи або події A, або події B, або обох їх одразу (одночасно). Теорема. Імовірність суми 2-х сумісних подій дорівнює сумі імовірностей цих подій без урахування їх спільної появи: p(A+B)=p(A)+p(B)−p(AB) Доведення: A+B=AB+AB+AB (сума несумісних пар) Тоді p(A+B)=p(AB)+p(AB)+p(AB) Подія A=AB+AB, Подія B=AB+AB p(A+B)=p(A)−p(AB)+p(B)−p(AB)+p(AB)=p(A)+p(B)−p(AB) Заувага: в цій теоремі може існувати 2 різні ситуації. p(A+B)=p(A)+p(B)−p(A)p(B), де A і B - незалежні; p(A+B)=p(A)+p(B)−p(A)p(B/A), де A і B - залежні;
У теорії імовірностей розрізняють прості і складені події. Наприклад, під час кидання костей у сумі випало 2 очка – це проста подія.
Подія називається складеною, якщо поява її залежить від появи інших, простих подій. Наприклад, під час кидання двох гральних кубиків у сумі випало 10 очок. Ця подія є складеною, бо вона може складатися з трьох простих подій:
на першому кубику випало 4, на 2-ому 6 очок;
2) на першому і на 2-ому випало по 5 очок;
Їх імовірності обчислюють через імовірності простих подій, в яких складаються складені. Таке обчислення спирається на застосування теорем додавання і множення несумісних однаково можливих подій, які утворюють повну групу, тобто елементарних подій. Теореми додавання і множення доведені для елементарних подій, а для інших, які не належать до елементарних подій, (а для інших які не належать до) ці теореми приймаються без доведення, тобто постулюються. Теорема: Імовірність суми двох несумісних подій дорівнює сумііморвіностей цих подій, тобто Р(А+В) = Р(А)+Р(В) Сумою подій А і В називає подія С, яка полягає у здійсненні під часодиничного випробування або подій А, або події В, або обох разом.Охарактеризувати умовні ймовірності та незалежні події Умо́вна ймові́рність — ймовірність однієї події за умови, що інша подія вже відбулася. Нехай
Властивості · Прямо з визначення очевидно випливає, що
· Якщо · Умовна ймовірність є ймовірністю, тобто функція
задовольняє всім аксіомам імовірнісної міри. У теорії ймовірностей дві випадкові події називаються незалежними, якщо настання однієї з них не змінює вірогідність настання іншої. Аналогічно, дві випадкові величини називають незалежними якщо значення однієї з них не впливає на розподіл значень іншої. [ред.]Незалежні події Вважатимемо, що дано фіксований ймовірнісний простір Означення 1. Дві події
Зауваження 1. В тому випадку, якщо ймовірність однієї події, скажемо
тобто умовна ймовірність події Означення 2. Нехай є сімейство (скінченне або нескінченне) випадкових подій
Означення 3. Нехай є сімейство (скінчене або нескінчене) випадкових подій
Охарактеризувати ймовірність настання хоча б однієї події Випадковою подією називається подія, яка може відбутися або не відбутися під час здійснення певного випробування. Імовірність — це числова характеристика можливості настання випадкової події за певної умови, яка може бути відтворена необмежену кількість разів. Імовірністю випадкової події називається відношення кількості елементарних подій, які сприяють цій події, до кількості всіх однаково можливих несумісних подій, які утворюють повну групу подій під час певного випробування. Імовірність події знаходять за формулою P дорівнює відношенню чисел m і n, де n — загальна кількість однаково можливих і несумісних подій, які утворюють повну групу; m — число елементарних подій, які сприяють події 15 охарактеризувати формулу повної ймовірності
|
|||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 335; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.200.56 (0.007 с.) |

 — фіксований ймовірнісний простір. Нехай
— фіксований ймовірнісний простір. Нехай 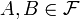 дві випадкової події, причому
дві випадкової події, причому 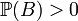 . Тоді умовною ймовірністю події
. Тоді умовною ймовірністю події  при умові події
при умові події 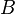 називається
називається

 , то умовна ймовірність, строго кажучи, не визначена. Проте іноді умовляються вважати її в цьому випадку рівною нулю.
, то умовна ймовірність, строго кажучи, не визначена. Проте іноді умовляються вважати її в цьому випадку рівною нулю. , задана формулою
, задана формулою
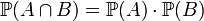 .
.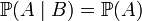 ,
,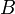 дорівнює безумовній вірогідності події
дорівнює безумовній вірогідності події 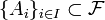 , де
, де 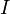 — довільна індексна безліч. Тоді ці події є попарно незалежними, якщо будь-які дві події з цього сімейства незалежні, тобто
— довільна індексна безліч. Тоді ці події є попарно незалежними, якщо будь-які дві події з цього сімейства незалежні, тобто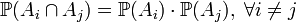 .
.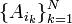 вірно:
вірно: .
.


