Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формула повної ймовірності дозволяє обчислити ймовірність деякої події через умовні ймовірності цієї події в припущенні якихось гіпотез, а також ймовірностей цих гіпотез. ВизначенняСодержание книги
Поиск на нашем сайте
Нехай дано імовірнісний простір
Зауваження Формула повної ймовірності також має наступну інтерпретацію. Нехай
Тоді
тобто апріорна ймовірність події рівна середньому його апостеріорної ймовірності. Охарактеризувати фолмулу Баєса Теоре́ма Ба́єса — одна з основних теорем теорії ймовірностей, яка визначає ймовірність настання події, коли відома тільки часткова інформація про подію. Названа на честь Томаса Баєса(/ beɪz / (1701-1761)). У теорії ймовірностей і статистиці, теорема Байеса (закон Байеса або ж правило Байєса) це теорема з двома різними інтерпретаціями. В байєсівсій інтерпретації, раціонально виразити, суб'єктивну ступінь віри у разі зміни показань для обліку. У "частотній інтерпретації", теорема стосується подання зворотної ймовірності двом подіям. В байєсівській інтерпретації, теорема Байеса має основоположне значення для байєсівської статистики та програми в полях у тому числі науки, техніки, медицини та права. Реалізація теореми Байеса для поновлення висновоків про ймовірності називається байєсівським висновком. який запропонував використовувати першу теорему оновити вірування. Тим не менш, історичні праці, опубліковані посмертно WAS. Його ідеї отримали обмежений вплив, поки не були відкриті заново і далі Top самостійно розроблений Лапласа, хто вперше опублікований сучасної формулюванні в історію 1812 Аналітична теорія ймовірностей. До другої половини 20-го століття, байєсовський інтерпретації залучила широке незгоду [правити] від спільноти математики займав частотної переглядів цілому [правити] Відмова Bayesianism як ненаукові. Тим не менш, у даний час широко прийнято. Це може бути викликано були розвиток обчислювальної техніки, які дозволили успішно Застосування Bayesianism до багатьох складних проблем Формула Баєса:
де
Формула виводиться із визначення умовної ймовірності:
Наслідок Важливим наслідком формули Баєса є формула повної ймовірності події, що залежить від декількох несуміснних гіпотез (і тільки від них).
Охарактеризувати схему Беруллі Проводяться n дослідів, у кожному з яких може настати певна подія («успіх») з ймовірністю p (або не настати — «неуспіх» — q = 1 — p). Задача — знайти ймовірність отримати k успіхів у досліді. Розв'язок:
Кількість успіхів — випадкова величина, що має розподіл Бернуллі. Властивості Нехай p — ймовірність успіху в схемі Бернуллі, q=1-p.Тоді найімовірнішою серед подій
18 охарактеризувати формулу Пуасона Формула Пуассона дає приблизне значення імовірності
Значить Охарактеризувати локальну теорему Муавра Лапласса Локальна теорема Муавра — Лапласа описує наближення нормального розподілу до біноміального розподілу. Є окремим випадком центральної граничної теореми. Теорема Якщо
Гранична форма теореми стверджує, що
для Можливо, формулювання стає ясним не відразу, проте практичний зміст теореми простий: при великих значеннях n імовірність спостерігаючи рівно m успіхів можна приблизно розраховувати за формулою:
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 216; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.156.26 (0.007 с.) |

 , і повна група подій
, і повна група подій  , таких що
, таких що  . Хай
. Хай  подія, що цікавить нас. Тоді
подія, що цікавить нас. Тоді .
.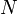 - випадкова величина, що має розподіл
- випадкова величина, що має розподіл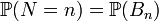 .
.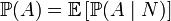 ,
,
 — апріорна ймовірність гіпотези A;
— апріорна ймовірність гіпотези A; — ймовірність гіпотези A при настанні події B (апостеріорна ймовірність);
— ймовірність гіпотези A при настанні події B (апостеріорна ймовірність); — ймовірність настання події B при істинності гіпотези A;
— ймовірність настання події B при істинності гіпотези A; — ймовірність настання події B.
— ймовірність настання події B.
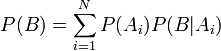 — ймовірність настання події B, що залежить від гіпотез
— ймовірність настання події B, що залежить від гіпотез 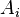 , якщо відомі їх ступені достовірності
, якщо відомі їх ступені достовірності
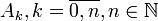 є подія
є подія  , де
, де 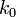 можна знайти з нерівності
можна знайти з нерівності 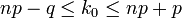 .
.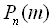 в тому випадку, коли число випробувань n велике, а імовірність p=P(А) в кожному з окремих випробувань маленька, оскільки добуток цих чисел
в тому випадку, коли число випробувань n велике, а імовірність p=P(А) в кожному з окремих випробувань маленька, оскільки добуток цих чисел 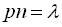 є заданим числом, незалежним від n, а значить
є заданим числом, незалежним від n, а значить 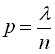 , досить мале. Тоді
, досить мале. Тоді  , m =0, 1, 2,…, n. Сума всіх ймовірностей дорівнює:
, m =0, 1, 2,…, n. Сума всіх ймовірностей дорівнює:
 де
де  . Одержано формулу Пуассона або закон Пуассона. Цей закон дає можливість наближати біноміальний розподіл при великій кількості випробувань і малій імовірності події А в кожному випробуванні.
. Одержано формулу Пуассона або закон Пуассона. Цей закон дає можливість наближати біноміальний розподіл при великій кількості випробувань і малій імовірності події А в кожному випробуванні. , тоді для k в
, тоді для k в  -околі точки np, існує наближення[1]
-околі точки np, існує наближення[1]