
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Охарактеризувати випадкові величини та функції розподілуСодержание книги
Поиск на нашем сайте
Випадкова величина є одним з основних понять теорії ймовірностей Означення · Випадковою величиною є будь-яка (не обов'язково числова) змінна Множина Властивості Випадкова величина X — це вимірна функція, визначена на даному вимірному просторі
Нехай x 1, x 2, … — значення випадкової величини X. Одне і те саме значення x j може відповідати, взагалі кажучи, різним елементарним подіям. Множина усіх цих елементарних подій утворює складену випадкову подію, що полягає в тому, що X = x j. Ймовірність цієї події позначається
визначає розподіл ймовірностей (слід відрізняти від функції розподілу ймовірностей) випадкової величини X. Очевидно, що:
Якщо дві або більше випадкових величини X 1, X 2, …, X n визначено на одному просторі елементарних подій, то їх спільний розподіл задається системою рівнянь, в яких всім комбінаціям Випадкові величини називаються незалежними, якщо для довільної комбінації значень
Тобто, якщо X k залежить лише від k -го випробування, то випадкові величини X 1, X 2, …, X n взаємно незалежні. Ймовірність випадкової величини · Ймовірність випадкової величини
де
Функція розподілу ймовірностей — В теорії ймовірностей це функція, яка повністю описує розподіл ймовірностей випадкової величини. Нехай
називається функцією розподілу ймовірностей або кумулятивною функцією розподілу ймовірностей випадкової величини ξ. Вираз в правій частині рівності є ймовірністю того, що випадкова величина Функція розподілу ймовірностей — В теорії ймовірностей це функція, яка повністю описує розподіл ймовірностей випадкової величини. Нехай
називається функцією розподілу ймовірностей або кумулятивною функцією розподілу ймовірностей випадкової величини ξ. Вираз в правій частині рівності є ймовірністю того, що випадкова величина 21 охарактеризувати основні закони розподілу дискретних випадкових величин Законом розподілу дискретної випадкової величини на- зивають відповідність між можливими значеннями і їх імовірностями. Його задають таблично, графічно чи аналітич-но (у виді формул). Сума імовірностей закону розподілу дорівнює 1: ^pi=l або ^ pi = 1, якщо множина можливих значень дискретної випадкової величини зліченна. Дві випадкові величини називаються незалежними, якщо закон розподілу однієї з них не залежить від того, які можливі значення прийняла друга величина. В протилежному випадкувипадкові величини є залежними. Декілька випадкових вели-чин називаються взаємно незалежними, якщо закони розпо-ділу будь-якого числа з них не залежать від того, які можливі значення набула решта величин. Добутком незалежних випадкових величин Х та Y нази-вають випадкову величину ХY, можливі значення якої рівні всеможливим добуткам співмножників Х і Y. Імовірності цих добутків рівні добуткам імовірностей відповідних співмнож-ників. Якщо деякі добутки ХіГі рівні між собою, то імовірність цього добутку рівна сумі імовірностей цих добутків. Сумою випадкових величин Х і Y називають випадкову величину Х + Y, можливі значення якої рівні всеможливим су-мам з доданків Х та Y. Імовірності цих сум рівні добуткам імовірностей доданків; для залежних величин - добуткам імо-вірностей одного доданку на умовну імовірність другого, якщо деякі суми рівні між собою, то імовірність такої суми рівна сумі відповідних імовірностей доданків. Математичним сподіванням дискретної випадкової величини називають суму добутків всіх її можливих значень на їх імовірності: M(X) = xlpl +х2р2 +... + хпрп =^jxipi (4.1.1). Якщо дискретна випадкова величина Х приймає зліченну множину можливих значень, то М(Х) = /^ xtpt при умові, що ряд збігається абсолютно. Математичне сподівання при-близно рівне середньому арифметичному спостережних зна- чень випадкової величини: М(Х) «X. Властивості математичного сподівання: 1. Математичне сподівання сталої величини є сама ця стала: М{С) = С. Сталий множник можна виносити за знак математич-ного сподівання: М(СХ) = СМ(Х).3. Математичне сподівання добутку двох незалежних випадкових величин дорівнює добутку їх математичних сподівань: M(XY) = M{X)M{Y). Наслідок. Математичне сподівання добутку декількох взаємно незалежних випадкових величин дорівнює добутку їх математичних сподівань 4. Математичне сподівання суми двох випадкових величин дорівнює сумі їх математичних сподівань: М(Х + Y) =M(X) + M(Y). Наслідок 2. Математичне сподівання різниці двох випадкових величин дорівнює різниці їх математичних сподіваньДисперсією D(X) випадкової величини Х називають мате-матичне сподівання квадрата відхилення цієї величини від її математичного сподівання М(Х): D{X) =М[Х-М(Х)]2 (4.1.2). Дисперсія має розмірність квадратних одиниць вимірю-ваної величини. Щоб отримати розмірність міри розсіювання в одиницях вимірюваної величини розглядають квадратний корінь з дисперсії сг(Х) = -JD(X) (4.1.4), який називають середнім квадратичним відхиленням, або стандартом. Властивості дисперсії: 1. Дисперсія будь-якої випадкової величини невід’ємна: D(X) > 0.Наслідок. Для будь-якої випадкової величини (M(X))2 <M(X2). 2. Дисперсія сталої дорівнює нулю: D(C) = 0. 3. Сталий множник можна винести за знак дисперсії, під-нісши його до квадрату: D(CX) = C2D(X). 4. Дисперсія суми двох незалежних випадкових величин дорівнює сумі їх дисперсій: D(X + Y) = D(X) + D(Y). Наслідок 1. Дисперсія суми попарно незалежних випад-кових величин ХиХ2,... Хn незалежних у сукупності, дорівнює сумі їх дисперсій: D{XX + X2 +... + Xn) = D{XX) + D(X2) +... + + D(Xn). Наслідок 2. Дисперсія суми постійної величини і випад-кової дорівнює дисперсії випадкової величини: D(C + X) = = D(X). 5. Дисперсія різниці двох незалежних випадкових вели- чин дорівнює сумі їх дисперсій: D(X - Y) = D(X) + D(Y). Теорема. Середнє квадратичне відхилення суми скінчен-ного числа взаємно незалежних випадкових величин дорівнює квадратному кореню з суми квадратів середніх квадратичних відхилень цих величин: сг(X1+X2+... + Xn) = л/сг2(X1) + сг2(X2) +... + сг2(Xn) (4.1.5). Якщо декілька випадкових величин мають однакові розподіли, то їх числові характеристики (математичне сподівання, дисперсія, і т. д.) однакові.
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 311; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.88.155 (0.014 с.) |

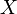 , "значення" якої
, "значення" якої  утворюють множину
утворюють множину  елементарних подій, або, іншими словами, позначають точки в просторі вибірок. Відповідний розподіл імовірностей називається розподілом випадкової величини
елементарних подій, або, іншими словами, позначають точки в просторі вибірок. Відповідний розподіл імовірностей називається розподілом випадкової величини  , тобто, вона визначається шляхом зіставлення кожної елементарної події з деякимдійсним числом. Більш формально:
, тобто, вона визначається шляхом зіставлення кожної елементарної події з деякимдійсним числом. Більш формально: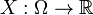 називається випадковою величиною, якщо
називається випадковою величиною, якщо  , де
, де  --
-- 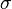 -алгебра Борелевих множин на
-алгебра Борелевих множин на  .
.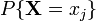 . Система рівнянь:
. Система рівнянь:
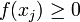 та
та 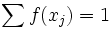 .
. ,
, 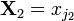 і т. д. призначаються визначені ймовірності.
і т. д. призначаються визначені ймовірності.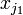 ,
,  , …,
, …, 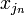 виконується рівність:
виконується рівність: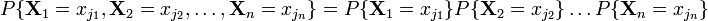

 ;
; 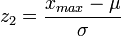 — граничні значення нормованої величини
— граничні значення нормованої величини 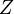 ;
; — це середнє значення величини
— це середнє значення величини 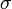 — cтандартне відхилення цієї величини.
— cтандартне відхилення цієї величини. — ймовірнісний простір, в якому
— ймовірнісний простір, в якому 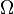 — множина елементарних подій,
— множина елементарних подій, 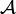 — сукупність підмножин
— сукупність підмножин 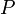 — міра на
— міра на 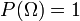 . Функція
. Функція 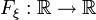 , визначена
, визначена 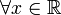 рівністю
рівністю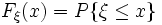 ,
,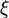 набуває значень менших або рівних
набуває значень менших або рівних  .
.


