
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Використання геометричної ймовірностіСодержание книги
Поиск на нашем сайте
· Голка Бюффона: Яка ймовірність того, що голка кинута на поверхню розграфлену паралельними прямими розташованими через однакові проміжки перетне одну з цих прямих? · Парадокс Бертрана: Яке матсподівання довжини випадково обраної хорди на одиничному колі? · Яка ймовірність того, що три випадково обрані на площині точки формують гострокутній трикутник? · Та подібні... Формально Стохастичний експеримент полягає в обранні навмання точки з множини
де Так визначену ймовірність назвемо геометричною (зрозуміло, що множина 42. Охарактеризувати незалежність подій У теорії ймовірностей дві випадкові події називаються незалежними, якщо настання однієї з них не змінює вірогідність настання іншої. Аналогічно, дві випадкові величини називають незалежними якщо значення однієї з них не впливає на розподіл значень іншої. Незалежні події Вважатимемо, що дано фіксований ймовірнісний простір Означення 1. Дві події
Зауваження 1. В тому випадку, якщо ймовірність однієї події, скажемо
тобто умовна ймовірність події Означення 2. Нехай є сімейство (скінченне або нескінченне) випадкових подій
Означення 3. Нехай є сімейство (скінчене або нескінчене) випадкових подій
Приклад 1. Монета кидається двічі. Ймовірність появи герба в першому випробуванні не залежить від появи чи непояви герба в другому випробуванні. В свою чергу, ймовірність появи герба в другому випробуванні не залежить від результатів першого випробування. Отже, події А — «поява герба в першому випробуванні» і В — «поява герба в другому випробуванні» — незалежні. 43 Охарактеризувати теорему множення ймовірностей. Добутком двох подій А і В називається подія С, що полягає у здійсненні під час одиничного випробовування й події А, і події В. Подія А називається від події В, якщо ймовірність події А не залежить від того, відбулась чи ні подія В. Дві події А та В називають залежними, якщо ймовірність настання однієї з них залежить від того, настала друга подія чи ні. Умовною ймовірністю РА(В) події В називається ймовірність події В, знайдена в припущенні, що подія А вже настала. З означення назалежних подій випливає, що настання однієї з них не змінює ймовірності настання другої. Тому для незалежних подій справджуються рівності:
Отже, умовні ймовірності незалежних подій дорівнюють їх безумовним імовірностям. Теорема 1. Імовірність добутку двох залежних подій А і В дорівнює добутку ймовірності однієї з них на умовну ймовірність другої, яка знайдена з припущенням того, що перша подія настала, тобто
Доведення. Нехай з усієї кількості n елементарних подій k сприяють події А і нехай з цих подій l сприяють події В, а, отже і події АВ. Тоді:
що й треба було довести. Теорема 2. Імовірність добутку двох незалежних подій А і В дорівнює добутку імовірностей цих подій, тобто
Доведення. Якщо А і В - незалежні події, то
і формула
перетворюється в формулу
44. Охарактеризувати формулу Бернуллі та алгоритм розв’язування задач за допомогою неї. У теорії ймовірності, формула Бернуллі дозволяє обчислити ймовірність успіхів у серії незалежних експериментів. Якщо ймовірність
Умови використання Якщо відбувається декілька випробувань, причому ймовірність події А в кожному з випробувань не залежить від результатів інших випробувань, то такі випробування називають незалежними відносно події А. В різних незалежних випробуваннях подія А може мати або різні ймовірності, або одну й ту ж саму ймовірність. Будемо розглядати тільки варіант зі сталою ймовірністю. Нехай відбувається n незалежних випробувань, в кожному з яких подія А може з'явитися або не з'явитися. Домовимося вважати, що ймовірність події А в кожному з випробувань стала, а саме дорівнює p. Тоді, ймовірність ненастання події А в кожному з випробувань також стала і дорівнює q = 1 - p. Поставимо собі задачу обчислити ймовірність того, що при n випробуваннях подія А відбудеться рівно k разів і, відповідно, не відбудеться n - k разів. Важливо підкреслити, що не вимагається, щоб подія А повторилась рівно k разів в певній послідовності. Поставлену задачу можно вирішити за допомогою формули Бернулі. Виведення формули Бернуллі Імовірність однієї складної події, яке полягає в тому, що в n випробуваннях подія А настане рівно k разів і не настане n - k разів, за теоремою множення незалежних подій дорівнює
Приклад задач Задача 1 Прилад складається з 10 компонент. Надійність (імовірність безвідмовної роботи протягом часу t) для кожної з компонент дорівнює p. Компоненти виходять з ладу незалежно одна від одної. Знайти ймовірність того, що за час t: · а) відмовить рівно одна компонента · б) відмовлять рівно дві компоненти Відповіді: · а) · б)
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 282; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.171.86 (0.006 с.) |

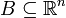 . За його математичну модель прийнято розглядати ймовірнісний простір
. За його математичну модель прийнято розглядати ймовірнісний простір 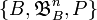 , де
, де 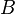 - борелева множина з
- борелева множина з  ,
, 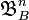 - клас борелевих підмножин множини
- клас борелевих підмножин множини 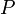 - ймовірність на класі
- ймовірність на класі  з цього класу визначається рівністю:
з цього класу визначається рівністю: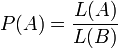 ,
,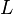 - міра Лебега на
- міра Лебега на 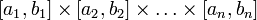 , дорівнює
, дорівнює 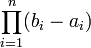 ).
). .
. .
.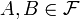 називають незалежними, якщо
називають незалежними, якщо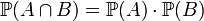 .
.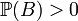 , визначення незалежності еквівалентне:
, визначення незалежності еквівалентне: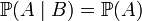 ,
,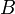 дорівнює безумовній вірогідності події
дорівнює безумовній вірогідності події 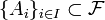 , де
, де 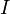 — довільна індексна безліч. Тоді ці події є попарно незалежними, якщо будь-які дві події з цього сімейства незалежні, тобто
— довільна індексна безліч. Тоді ці події є попарно незалежними, якщо будь-які дві події з цього сімейства незалежні, тобто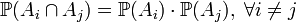 .
.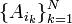 вірно:
вірно: .
.


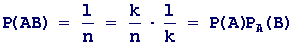

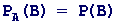
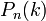 того, що подія
того, що подія 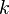 разів в
разів в 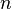 незалежних випробуваннях дорівнює
незалежних випробуваннях дорівнює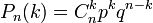 або
або
 . Таких складних подій може бути стільки, скільки можливо скласти комбінацій з n елементів по k елементам, тобто
. Таких складних подій може бути стільки, скільки можливо скласти комбінацій з n елементів по k елементам, тобто  . Так як ці складні події несумісні, то за теоремою додавання ймовірностей несумісних подій шукана ймовірність дорівнює сумі ймовірностей всіх можливих складних подій. Так як імовірності всіх цих складних подій однакові, то шукана ймовірність (поява k разів події А в n випробуваннях) дорівнює ймовірності однієї складної події, помноженої на їх кількість:
. Так як ці складні події несумісні, то за теоремою додавання ймовірностей несумісних подій шукана ймовірність дорівнює сумі ймовірностей всіх можливих складних подій. Так як імовірності всіх цих складних подій однакові, то шукана ймовірність (поява k разів події А в n випробуваннях) дорівнює ймовірності однієї складної події, помноженої на їх кількість:




