
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Охарактеризувати нульову гіпотезу та алгоритм перевірки правильності нульової гіпотези.Содержание книги
Поиск на нашем сайте
Нульова́ гіпо́теза — наукове припущення, що перевіряється емпіричними дослідженнями на неспроможність (чи навпаки спроможність) відобразити реальність. Поняття нульової гіпотези часто використовується в статистичних методиках, зокрема такими науками, як біологія, медицина, соціологія. Нульова гіпотеза це бездоказове припущення здійсненне до проведення дослідження. Поняття нульової гіпотези передбачає існування альтернативної гіпотези, що її заперечує. Нульова гіпотеза зазвичай в роботах позначається H0, а альтернативна — H1. [1] На практиці нульовою гіпотезою слугує відсутність статистично значущої кореляції між якимись характеристиками чи показниками, а альтернативною є гіпотеза про існування кореляції. [2] Для людей практично завжди характерний суб'єктивізм — існування певного упередженого ставлення до будь-яких явищ, навіть цілком абстрактних. Тому більшість досліджень проводиться з певною метою і очікується підтвердження інтуїтивних чи моральних здогадок вчених (альтернативної гіпотези) про наявність статистично значущої кореляції поміж факторами. Нульова ж гіпотеза слугує протилежною точкою зору, яку дослідник намагається спростувати — довести, що одна характеристика таки має вплив на іншу. Проте емпірика часто доводить і вірність саме нульової гіпотези. У такому випадку дослідження показує інший результат, аніж очікувався. 57-58-59. Охарактеризувати властивості коефіцієнта кореляції Кореляція може бути позитивною та негативною (можлива також ситуація відсутності статистичного зв'язку - наприклад, для незалежних випадкових величин). Від'ємна кореляція – кореляція, при якій збільшення однієї змінної пов'язане зі зменшенням іншої, при цьому коефіцієнт кореляції від'ємний. Додатна кореляція – кореляція, при якій збільшення однієї змінної пов'язане зі збільшенням іншої, при цьому коефіцієнт кореляції додатній. Коефіцієнт кореляції Нехай
де:
Властивості Якщо X та Y — незалежні, то коефіцієнт кореляції Завжди виконується нерівність:[1]
Причому, 60. Охарактеризувати класичне та статистичне означення ймовірностей. Імовірністю події А називається відношення числа ре-зультатів випробування т, сприятливих до настання події А до загального числа всіх рівноможливих несумісних елемен- тарних подій п, що утворюють повну групу: Р(А) = — (1.4.1). п Для кожної випадкової події icD має місце така її основна властивість: 0 < Р(А) < 1, оскільки т = 0,1,2,... = п. Причому, імовірність неможливої події дорівнює 0: Р(0)= = 0; імовірність достовірної (вірогідної) події дорівнює 1: P(Q) = 1. Відносною частотою події А називають відношення числа випробувань т, в яких подія відбулась до загального числа проведених випробувань п: W(A) = — (1.4.2). пІмовірність обчислюють з теоретичних міркувань, віднос-ну частоту – після проведення випробування. Як і імовір-ність, відносна частота знаходиться в межах: 0 ≤W(A) ≤1. Відносну частоту або число, близьке до неї, приймають за статистичну імовірність події. Статичне означення ймовірностей татистична ймовірність (the statistical probability) має властивості: 1) Р(А) 2) для вірогідної події 3) якщо події А і В несумісні, то статистична імовірність події С=А+В дорівнює сумі статистичних ймовірностей Р(А+В)=Р(А)+Р(В). Легко бачити, що формулою (1) можна користуватись лише у випадку скінченних m i n. Якщо m і n нескінченні, то класична імовірність вводиться аксіоматично. Класичною імовірністю Р(А) події А, яка визначається простором елементарних подій 1) Р(А) 2) 3) для несумісних подій А і В: Р(А+В)=Р(А)+Р(В). Умови 1) - 3) отримали назву аксіом теорії ймовірностей. Аксіоматичне означення класичної ймовірності зручне в теорії, проте воно не дає способу її обчислення. Такий спосіб дає визначення класичної ймовірності як границі статистичної. Якщо проводяться серії однотипних дослідів, в кожній з яких обчислені статистичні ймовірності, то отримаємо послідовність { Р1*(А), Р2*(А),... Рn*(А) }, границя якої і визначає класичну ймовірність при Введення класичного означення ймовірності відбулося не в результаті однократної дії, а зайняло певний проміжок часу, як і формування самої теорії ймовірностей. Тобто відбувалося безперервне вдосконалення формування, перехід від конкретних задач до загального випадку. Найперші роботи, котрі були присвячені теорії ймовірності як науці, були написані Х. Гюйгенсом (1657) «Про розрахунки в азартних іграх». Однак у своїй праці автор не дає чіткого формулювання для класичного означення ймовірності. Це поняття було введено, хоча і в недосконалій формі, Я. Бернуллі (1713) у трактаті «Мистецтво припущень»: «Імовірність – ступінь вірогідності і відрізняється від неї, як частина від цілого». Як бачимо, таке формулювання є досить узагальненим. Однак у п’ятій главі четвертої частини своєї роботи Я. Бернуллі описує класичну ймовірність як відношення числа «щасливих» випадків до кількості усіх можливих. Якобом Бернуллі було запропоновано й інше означення ймовірності як відношення кількості «щасливих» випадків до кількості «нещасливих». Однак в науці це означення не було прийняте з двох причин: 1) неадитивності відношень (першого та другого означень); 2) зміна відношення в останньому означенні від 0 до ∞.
|
|||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 328; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.255.183 (0.006 с.) |

 та
та  — випадкові величини з математичним сподіванням μ X та μ Y. Їх коефіцієнт кореляції позначається як
— випадкові величини з математичним сподіванням μ X та μ Y. Їх коефіцієнт кореляції позначається як  і дорівнює:[1]
і дорівнює:[1]
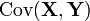 — коваріація величин
— коваріація величин 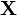 та
та 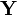 ,
, — стандартне відхилення величин
— стандартне відхилення величин 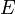 — оператор математичного сподівання.
— оператор математичного сподівання. дорівнює 0. Зворотне твердження невірне. Коефіцієнт кореляції може дорівнювати 0 навіть якщо Y є функцією від X. [1]
дорівнює 0. Зворотне твердження невірне. Коефіцієнт кореляції може дорівнювати 0 навіть якщо Y є функцією від X. [1] .
. тоді і лише тоді, коли
тоді і лише тоді, коли  , де a та b — сталі.
, де a та b — сталі. 0 це очевидно, оскільки m
0 це очевидно, оскільки m 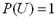 ;
; , називається числова функція, яка задовольняє такі умови:
, називається числова функція, яка задовольняє такі умови: ;
; ;
; .
.


