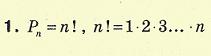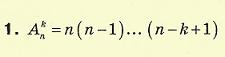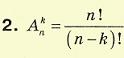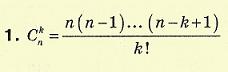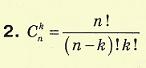Число елементів скінченної множини a завжди більша від числа елементів його власної підмножини B.

Для множин можна ввести ряд операцій (теоретико-множинних операцій),

результатом виконання яких будуть також множини. За допомогою цих

операцій можна конструювати із заданих множин нові множини.

а) Об’єднанням множин A і B (позначається A(B) називається множина тихелементів, які належать хоча б одній з множин A чи Bб) Перетином множин A і B (позначається A(B) називається множина, щоскладається з тих і тільки тих елементів, які належать множинам A і Bодночаснов). Різницею множин A і B (записується A\B) називається множина тихелементів, які належать множині A і не належать множині B.г). Симетричною різницею множин A і B (записується A(B, A(B або A(B)називається множина, що складається з усіх елементів множини A, які немістяться в B, а також усіх елементів множини B, які не містяться в A.

Охарактиризувати предмет комбінаторики

Комбінато́рика (Комбінаторний аналіз) — розділ математики, присвячений розв'язанню задач вибору та розташування елементів деякої, зазвичай скінченної, множини відповідно до заданих правил. Кожне таке правило визначає спосіб побудови деякої конструкції із елементів вихідної множини, що зветься комбінаторною конфігурацією. Тому на меті комбінаторного аналізу стоїть дослідження комбінаторних конфігурацій, алгоритмів їх побудови, оптимізація таких алгоритмів, а також розв'язання задач переліку.

Найпростішими прикладами комбінаторних конфігурацій є перестановки, розміщення, комбінація та розбиття.

Комбінаторика пов'язана з багатьма іншими розділами математики.

Термін «комбінаторика» ввів Лейбніц, який у 1666 році опублікував свою працю «Міркування про комбінаторне мистецтво».

Іноді під комбінаторикою розуміють більш широкий розділ дискретної математики, що включає теорію графів.

Приклади комбінаторних конфігурацій і завдань

Для формулювання і розв'язання комбінаторних задач використовують різні моделі комбінаторних конфігурацій. Прикладами комбінаторних конфігурацій є:

Розміщенням з n елементів по k називається упорядкований набір з k різних елементів деякого n-елементного безлічі.
Перестановкою з n елементів (наприклад чисел 1,2,..., n) називається всякий упорядкований набір з цих елементів. Перестановка також є розміщенням з n елементів по n.
Поєднанням з n по k називається набір k елементів, вибраних з даних n елементів. Набори, що відрізняються тільки порядком проходження елементів (але не складом), вважаються однаковими, цим поєднання відрізняються від розміщень.
Композицією числа n називається всяке уявлення n у вигляді впорядкованої суми цілих позитивних чисел.
Розбиттям числа n називається всяке уявлення n у вигляді невпорядкованою суми цілих позитивних чисел.

Прикладами комбінаторних задач є:

Скількома способами можна розмістити n предметів по m шухлядах так, щоб виконувалися задані обмеження?
Скільки існує функцій F з m-елементного безлічі в n-елементне, що задовольняють заданим обмеженням?
Скільки існує різних перестановок з 52 гральних карт?

Відповідь: 52! (52 факторіал), тобто, 80658175170943878571660636856403766975289505440883277824000000000000 або приблизно 8,0658 × 1067.

При грі в кістки кидаються дві кістки, і випали окуляри складаються; скільки існує комбінацій, таких, що сума очок на верхніх гранях дорівнює дванадцяти?

Рішення: Кожен можливий результат відповідає функції F: \ {1, 2 \} \ to \ {1, 2, 3, 4, 5, 6 \} (аргумент функції - це номер кістки, значення - окуляри на верхній грані). Очевидно, що лише 6 +6 дає нам потрібний результат 12. Таким чином існує лише одна функція, яка ставить у відповідність 1 число 6, і 2 число 6. Або, іншими словами, існує всього одна комбінація, така, що сума очок на верхніх гранях дорівнює дванадцяти.

Розділи комбінаторики
Перечислительного комбінаторика

Перечислительного комбінаторика (або обчислюється комбінаторика) розглядає задачі про перерахування або підрахунку кількості різних конфігурацій (наприклад, перестановок) утворюваних елементами кінцевих множин, на які можуть накладатися певні обмеження, такі як: розрізнюваність або нерозрізненість елементів, можливість повторення однакових елементів і т. п.

Кількість конфігурацій, утворених декількома маніпуляціями над безліччю, підраховується згідно з правилами додавання і множення.

Типовим прикладом завдань даного розділу є підрахунок кількості перестановок. Інший приклад - відома Задача про листи.
Структурна комбінаторика

До даного розділу належать деякі питання теорії графів, а також теорії матроідов.
Екстремальна комбінаторика

Прикладом цього розділу може служити наступна задача: яка найбільша розмірність графа, який задовольняє певним властивостям.
Теорія Рамсея
Основна стаття: Теорія Рамсея

Теорія Рамсея вивчає наявність регулярних структур у випадкових конфігураціях елементів. Прикладом твердження з теорії Рамсея може служити наступне:

в групі з 6 чоловік завжди можна знайти трьох чоловік, які або попарно знайомі один з одним, або попарно незнайомі.

У термінах структурної комбінаторики це ж твердження формулюється так:

в будь-якому графі з 6 вершинами знайдеться або кліка, або незалежна безліч розміру 3.

Імовірнісна комбінаторика

Цей розділ відповідає на питання виду: яка вірогідність присутності певного властивості у заданої множини.
Топологічна комбінаторика

Топологічна комбінаторика (англ.) застосовує ідеї та методи комбінаторики в топології, при вивченні дерева прийняття рішень, частково впорядкованих множин, розмальовок графа і ін
Інфінітарная комбінаторика

Інфінітарная комбінаторика (англ.) - застосування ідей та методів комбінаторики до нескінченних (в тому числі, незліченною) множинам.

Охаректиризувати основні принципи комбінаторики

Двома основними правилами комбінаторики є:
Принцип суми. Якщо множина A містить m елементів, а множина B – n елементів, і ці множини не перетинаються, то А і B містить m+n елементів.
Принцип добутку. Якщо множина A містить m елементів, а множина B – n елементів, то A і B містить m на n елементів, тобто пар.
Кількість елементів множини A будемо далі позначати |A|.
Ці правила мають також вигляд:
Принцип суми. Якщо об'єкт A можна вибрати m способами, а об'єкт B – n іншими способами, то вибір "або A, або B" можна здійснити m+n способами.
Принцип добутку. Якщо об'єкт A можна вибрати m способами і після кожного такого вибору об'єкт B може бути вибраним n способами, то вибір "A і B" в указаному порядку можна здійснити m на n способами.
Наведені правила очевидним чином узагальнюються на випадки довільних скінченних об'єднань множин, що попарно не перетинаються, та на скінченні декартові добутки.
Правило добутку застосовується для підрахунку кількості об'єктів, що розглядаються як елементи декартових добутків відповідних множин. Отже, ці об'єкти являють собою скінченні послідовності – пари, трійки тощо.
Нагадаємо, що з точки зору математики послідовність довжини m елементів множини A – це функція, яка натуральним числам 1, 2, …, m ставить у відповідність елементи з A.

Перестановки

Нехай треба підрахувати число способів, за якими можна розмістити в ряд n предметів. Якщо дані предмети розглядати як елементи множини то кожне розміщення є скінченною множиною, елементи якої записано у певному порядку.

Скінченні множини, для яких істотним є порядок елементів, називаються впорядкованими. Вказати порядок розміщення елементів у скінченній множині з п елементів означає поставити у відповідність кожному елементу даної множини певне натуральне число від 1 до п.

Дві впорядковані множини називаються рівними, якщо вони складаються з тих самих елементів і однаково впорядковані. З цього випливає, що множини (а, b, с) і (b, с, а) - це різні впорядковані множини.

Означення. Будь-яка впорядкована множина, що складається з п елементів, називається перестановкою з п елементів.

Перестановки з п елементів складаються з одних і тих самих елементів, а відрізняються одна від одної лише порядком.

Розміщення

Нехай деяка множина складається з п різних елементів.

Означення. Розміщеннями з п елементів по k називаються підмножини, що мають k елементів, вибраних з даних п елементів і розміщених у певному порядку (k<п).

Розміщення можуть відрізнятися одне від одного або самими елементами, або порядком їх розміщення.

Сполучення