
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закони розподілу випадкових величинСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Випадковою називається величина, яка в результаті досліду може прийняти одне і тільки одне значення, що наперед невідоме і залежить від випадкових причин, які заздалегідь не можуть бути враховані. Дискретною називають випадкову величину, яка набуває окремих, ізольованих можливих значень з певною ймовірністю. Неперервною називають випадкову величину, яка може набувати всіх значень з деякого кінцевого або нескінченного проміжку. Приклади|зразки| дискретних випадкових величин: Ø кількість повернених в строк кредитів; Ø кількість договорів, за якими страхова компанія виплачує страхові суми; Ø кількість пакетів акцій, за якими буде отриманий прибуток. Приклади|зразки| неперервних випадкових величин: Ø сума прибутку, отриманого через рік; Ø вклади населення в даному банку. Законом розподілу випадкової величини називається всяке співвідношення, що встановлює зв'язок між можливими значеннями випадкової величини і відповідними їй ймовірностями. Закон розподілу можна задати: · у табличній формі (ряд розподілу);
· аналітично (у вигляді формули); ·
Графік, що відповідає заданому розподілу називається багатокутником розподілу випадкової величини. При цьому на осі абсцис відкладаються значення хi випадкової величини Х, а на осі ординат – їх ймовірності рi.
Розв’язання. Підприємець може не отримати кредит в жодному з банків, отримати в першому, у другому та у обох банках:
Перевірка: 0,28+0,42+0,12+0,18=1.
Функцією розподілу називають функцію
Властивості функції розподілу: 1. 2. 3. 4.
Розв’язання. Випадкова величина Х – число несвоєчасних розрахунків за продукцію – може приймати такі значення Для побудови графіка функції розподілу ймовірностей дискретної випадкової величини необхідно розрахувати кумулятивні (накопичені) ймовірності, що відповідають значенням випадкової величини. Алгоритм їх розрахунку витікає з сенсу функції розподілу
Ця формула справедлива для всіх F (хi), окрім F (х0). Оскільки функція розподілу визначає ймовірність того, що випадкова величина набуде значення, менше заданого, зрозуміло: ймовірність того, що випадкова величина прийме значення, не більш мінімального, дорівнює 0, тобто F (х0) = 0. Якщо:
Щільністю розподілу ймовірності неперервної випадкової величини називають функцію - першу похідну від функції розподілу:
Властивості щільності розподілу: 1. 2. 3. 4. Неперервна випадкова величина може бути задана або функцією розподілу ймовірностей (інтегральна функція розподілу)
Знайти: 1) коефіцієнт а; 2) щільність ймовірностей 3) ймовірність попадання величини Х в інтервал (2,5; 3,5). Розв’язання.
Враховуючи вигляд f (x), дістанемо
Отже,
Розв’язання. Відомо, що 1. При 2. При
= 3. При
= Отже,
Побудуємо графік

Числові характеристики випадкових величин Математичне сподівання Математичним сподіванням
для дискретної випадкової величини,
для неперервної випадкової величини, причому припускається, що ряд і інтеграл збігаються абсолютно. У цих формулах
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 561; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.56.181 (0.01 с.) |


 x 1
x 1

 ;
; графічно.
графічно.
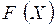 , яка визначає ймовірність того, що випадкова величина
, яка визначає ймовірність того, що випадкова величина  в результаті випробування набуває значення, меншого за
в результаті випробування набуває значення, меншого за 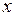 , тобто
, тобто . (2.1)
. (2.1)
 , якщо
, якщо 
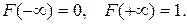



 , тоді
, тоді 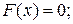
 , тоді
, тоді 
 , тоді
, тоді 
 , тоді
, тоді 


 . (2.2)
. (2.2)
 , зокрема
, зокрема 

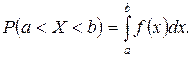 (2.3)
(2.3)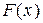 , або функцією щільності ймовірностей (диференціальна функція розподілу)
, або функцією щільності ймовірностей (диференціальна функція розподілу)  .
.


 Звідси:
Звідси:



 Побудувати функцію
Побудувати функцію  . Знайдемо значення цієї функції на кожному інтервалі окремо:
. Знайдемо значення цієї функції на кожному інтервалі окремо:



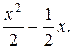
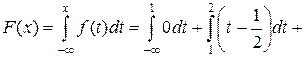






 (2.4)
(2.4) (2.5)
(2.5) – їх ймовірності,
– їх ймовірності,  щільність ймовірності.
щільність ймовірності.


