
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Система двох дискретних випадкових величин.Содержание книги
Поиск на нашем сайте
На одному й тому самому просторі елементарних подій W можна визначити не одну, а кілька випадкових величин. Така потреба постає, наприклад, коли досліджуваний об’єкт характеризується кількома випадковими параметрами. Сукупність випадкових величин Одночасна поява внаслідок проведення експерименту n випадкових величин (X1, X2, …, Xn) з певною ймовірністю являє собою n-вимірну випадкову величину, яку називають також системою n випадкових величин, або n-вимірним випадковим вектором. _________________________________
Закон розподілу ймовірностей дискретної двомірної величини. Законом розподілу двох дискретних випадкових величин називають перелік можливих значень Y = yi , X = xj та відповідних їм імовірностей спільної появи. У табличній формі цей закон має такий вигляд:
Тут використано такі позначення
Умова нормування має такий вигляд:
_________________________________
Коефіцієнт кореляції та його властивості. Під час вивчення системи двох і більше випадкових величин доводиться з’ясовувати наявність зв’язку між цими величинами та його характер. З відповідною метою застосовують так званий кореляційний момент:
У разі Κху = 0 зв’язок між величинами Х та Y відсутній. Тісноту кореляційного зв’язку характеризує коефіцієнт кореляції:
Якщо випадкові величини Х та Y є незалежними, то Κху = 0 і rху = 0. Рівність нулеві rху є необхідною, але не достатньою умовою незалежності випадкових величин. Дві випадкові величини Х і Y називають некорельованими, якщо rху = 0, і корельованими, якщо rху ¹ 0. _________________________________
Функція розподілу ймовірностей системи двох випадкових величин та її властивості. Функцією розподілу ймовірностей системи двох випадкових величин (Х, Y) називають таку функцію двох аргументів х, у, яка визначає ймовірність спільної появи подій (X < x) I (Y < y):
F(x,y) = P((X < x) I (Y < y)). Властивості F(x, y) 1. 0 £ F(x, y) £ 1, оскільки 0 £ P((X < x) I (y < y)) £ 1. 2. Якщо один із аргументів F(x, y) прямує до +
3. 4. 5. F(x, y) є неспадною функцією аргументів х і у. Р(а < Х < b, Y < y) = F(b, y) – F(a, y); P(X < x, c < Y < d) = F(x, d) – F(x, c). 6. Імовірність влучення точки (Х, Y) в довільний прямокутник (a < X< b, c < Y < d) обчислюємо так: P(a < x < b, c < y < d) = F(b, d) + F(a, c) – F(a, d) – F(b, c). _________________________________
Щільність розподілу двомірної випадкової величини. Характеристикою системи неперервних випадкових величин є щільність імовірностей.
Функція f (x, y) може існувати лише за умови, що F (x, y) є неперервною за аргументами х і у та двічі диференційовною. Властивості f (x, y) 1. Функція f (x, y) ³ 0, оскільки F(x, y) є неспадною відносно аргументів х і у. 2. Умова нормування системи двох неперервних випадкових величин (Х, Y) така:
3. Імовірність розміщення системи змінних (х, у) в області
4. Функція розподілу ймовірностей системи двох змінних визначається з рівняння
5. Якщо
_________________________________
Основні числові характеристики системи двох неперервних випадкових величин (Х,У).
_________________________________
Ймовірність влучення випадкових точок у прямокутник. Імовірність влучення точки (Х, Y) в довільний прямокутник (a < X< b, c < Y < d) обчислюємо так: P(a < x < b, c < y < d) = F(b, d) + F(a, c) – F(a, d) – F(b, c). Доведення. Розглянемо такі випадкові події: A = (X < b, Y < d); B = (X < a, Y < c); C = (a < X < b, Y < c); D = (X < a, c < Y < d); E = (a < X < b, c < Y < d). Оскільки випадкові події B, C, D, E несумісні, маємо: A = B U C U D U E. P(A) = P(B U C U D U E) = P(B) + P(C) + P(D) + P(E). P(x < b, y < d) = P(x < a, y < c) + P(a < x < b, y < c) + P(х < a, c < у < d) + P(a < x < b, c < y < d). F(b, d) = F(a, c) + F(b, c) – F(a, c) + F(a, d) – F(a, c) + P(a<X<b,c<Y<d); P(a<X<b,c<Y<d)=F(b,d)+F(a,c)–F(a, d) – F(b, c), що й треба було довести. _________________________________
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 248; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.95.120 (0.006 с.) |

 які розглядаються спільно, називається системою
які розглядаються спільно, називається системою  випадкових величин. Якщо
випадкових величин. Якщо  тобто розглядається система двох випадкових величин
тобто розглядається система двох випадкових величин  , то геометрично її можна тлумачити як випадкову точку з координатами
, то геометрично її можна тлумачити як випадкову точку з координатами  на площині
на площині  або як випадковий вектор, складові якого — випадкові величини
або як випадковий вектор, складові якого — випадкові величини 
 X=xj
Y=yi
X=xj
Y=yi

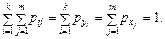


 , або
, або  .
. , то функція розподілу системи прямує до функції розподілу одного аргументу, що не прямує до +
, то функція розподілу системи прямує до функції розподілу одного аргументу, що не прямує до + 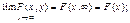

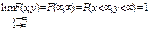


 .
. обчислюється так:
обчислюється так:

 , то
, то










