
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Класичне означення імовірності.Содержание книги Поиск на нашем сайте
Імовірністю випадкової події А називається невід’ємне число Р(А), що дорівнює відношенню числа елементарних подій m (0≤ m ≤ n), які сприяють появі А, до кількості всіх елементарних подій n простору Ω: Р (А) = Для неможливої події Р (Æ) = 0; Для вірогідної події Р (Ω) = 1. Отже, для довільної випадкової події
_________________________________
Основні формули комбінаторики. Переставленням із n елементів називають такі впорядковані множини з n елементів, які різняться між собою порядком їх розміщення. Кількість таких упорядкованих множин, де всі елементи різні, обчислюється за формулою:
Розміщенням із n елементів по m (0
Комбінаціями з n елементів по
_________________________________
Геометрична ймовірність. Класичне означення ймовірності придатне лише для експериментів з обмеженим числом рівномірних елементарних подій, тобто коли множина W обмежена. Якщо простір елементарних подій W можна подати у вигляді деякого геометричного образу, а множину елементарних подій для події А — як частину цього геометричного образу, то ймовірність події А визначається як відношення мір цих множин:
При цьому вважається, що ймовірність попадання в деяку частину геометричного образу пропорційна до міри цієї його частини. _________________________________
Статистична ймовірність. На практиці обчислити ймовірності випадкових подій можна лише для обмеженого класу задач як для дискретних, так і для неперервних просторів елементарних подій. Для більшості задач, особливо економічних, обчислити ймовірності практично неможливо. У цьому разі використовується статистична ймовірність. Статистичною ймовірністю події А називається відношення кількості m випробувань, в яких подія А відбулась, до загальної кількості виконаних випробувань n: Знаходження статистичної ймовірності пов’язане з проведенням n випробувань, тому вона називається ще частістю, або відносною частотою, події.
Як і для ймовірності випадкової події, для відносної частоти виконується нерівність
Залежні та незалежні події. Умовна ймовірність. Випадкові події А і В називають залежними, якщо поява однієї з них впливає на ймовірність появи іншої. У противному разі випадкові події А і В називаються незалежними. Якщо ймовірність випадкової події А обчислюється за умови, що подія В відбулася, то така ймовірність називається умовною. Ця ймовірність обчислюється за формулою
Аналогічно
1. Р (А / В) = 0, якщо А∩В = Æ. 2. Р (А / В) = 1, якщо А∩В = В. 3. У решті випадків 0 < Р(А / В) < 1. _________________________________ Теорема складання ймовірностей несумісних подій. Нехай подія А є сумою двох подій В і С. Тоді, якщо події В і С несумісні, то
_________________________________
Теорема складання ймовірностей сумісних подій. Нехай подія А є сумою двох подій В і С. Тоді, якщо події В і С сумісні, то
_________________________________
Теорема множення ймовірностей для залежних подій. Нехай подія А є добутком двох подій В і С. Тоді, якщо події В і С залежні, то
Ці теореми справджуються й для добутку n (n > 2) подій. _________________________________
Теорема множення ймовірностей для незалежних подій. Нехай подія А є добутком двох подій В і С. Тоді, якщо події В і С незалежні, то
Ці теореми справджуються й для добутку n (n > 2) подій. _________________________________ Формула повної ймовірності. У разі, коли випадкова подія А може відбутися лише за умови, що відбудеться одна з несумісних випадкових подій Ві, які утворюють повну групу і між собою є попарно несумісними
яка називається формулою повної ймовірності. Випадкові події В1, В2,... Вn називають гіпотезами. _________________________________
Формула Байєса. Застосовуючи формулу множення ймовірностей для залежних випадкових подій А, Ві (і = Р(А) Р(Ві / А) = Р (Ві) Р(А / Ві) → Одержана залежність називається формулою Байєса. Її використовують для переоцінювання ймовірностей гіпотез Ві за умови, що випадкова подія А здійсниться. _________________________________ Формула Бернуллі. Якщо кожний експеримент має лише два несумісні наслідки зі сталими ймовірностями p і q, то їх називають експериментами за схемою Бернуллі. У кожному експерименті випадкова подія з імовірністю p відбувається, а з імовірністю q — не відбувається, тобто p + q = 1.
Імовірність того, що в результаті n незалежних експериментів за схемою Бернуллі подія А з’явиться m раз, подається у вигляді
Імовірність того, що в результаті n незалежних експериментів подія А з’явиться від mі до mj раз, обчислюється так:
_________________________________
|
||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 250; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.186.186 (0.01 с.) |

 .
.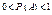 .
. .
. ) називаються такі впорядковані множини, кожна із яких містить m елементів і які відрізняються між собою порядком розташування цих елементів або хоча б одним елементом. Кількість таких множин, де всі елементи різні, обчислюється за формулою:
) називаються такі впорядковані множини, кожна із яких містить m елементів і які відрізняються між собою порядком розташування цих елементів або хоча б одним елементом. Кількість таких множин, де всі елементи різні, обчислюється за формулою: .
. називаються такі множини з m елементів, які різняться між собою хоча б одним елементом. Кількість таких множин:
називаються такі множини з m елементів, які різняться між собою хоча б одним елементом. Кількість таких множин: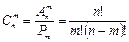 .
. .
.
 .
. _________________________________
_________________________________ ,
,  .
. ,
, 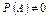 .
. .
.
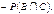

 .
. , імовірність події А обчислюється за формулою
, імовірність події А обчислюється за формулою ,
,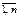 ), дістаємо
), дістаємо

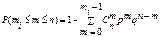 .
.


