
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функція 1-ого випадкового аргументу.Содержание книги Поиск на нашем сайте
Функцією випадкового аргументу Х називають таку випадкову величину Y, яка набуває значення Y = у = Коли Х є неперервною випадковою величиною, то і Y = 1) Нехай закон дискретної випадкової величини Х задано таблицею:
Тоді закон розподілу випадкової величини Y =
Умова нормування для f (у):
За знайденою f (у) функцією розподілу ймовірностей визначається
_________________________________
Математичне сподівання функції 1-ого випадкового аргументу. Функцією випадкового аргументу Х називають таку випадкову величину Y, яка набуває значення Y = у = Коли Х є неперервною випадковою величиною, то і Y = Математичне сподівання дискретного випадкового аргументу
Математичне сподівання функцій неперервного випадкового аргументу:
_________________________________
Функції 2-х випадкових аргументів. У загальному випадку функцію двох аргументів Х і Y можна позначити як
де Якщо Х та Y є дискретними випадковими величинами, то і Z буде дискретною. Якщо Х та Y є неперервними, то і Z буде неперервною.
_________________________________
Математичне сподівання суми двох випадкових аргументів. Математичне сподівання. М (Х + Y) = М (Х) + М (Y). (1) Висновок 1. М(АХ+ВY+С)=АМ(Х)+ВМ(Y)+С. А, В, С — деякі сталі. Висновок 2.
_________________________________
Біноміальний розподіл. Цілочислова випадкова величина X має біноміальний закон розподілу, якщо ймовірність її можливих значень обчислюється за формулою Бернуллі:
При перевірці виконання умови нормування використовується формула біному Ньютона, тому закон розподілу називають біноміальним:
Імовірнісна твірна функція для біноміального закону
Основні числові характеристики:
_________________________________
Закон розподілу неперервної випадкової величини. Рівномірний розподіл.
Цілочислова випадкова величина Х має рівномірний закон розподілу, якщо ймовірності її можливих значень обчислюються за формулою:
Імовірнісна твірна функція:
Числові характеристики:
_________________________________
Нормальний розподіл. Випадкова величина Х має нормальний закон розподілу ймовірностей, якщо f (х) = де а = М (X), s = s (X). Отже, нормальний закон визначається звідси параметрами а і s і називається загальним. Тоді F(x)=
Для нормального закону Мо=Ме=а. Загальний нормальний закон позначають: N (a; s). _________________________________
Правило трьох сигм для нормального закону. Коли
Практично ця подія при одному експерименті здійсниться, а тому її вважають практично вірогідною. Звідси:
Тобто ймовірність того, що внаслідок проведення експерименту випадкова величина Х, яка має закон розподілу N (a; s), не потрапить у проміжок _________________________________
Геометричний закон. Закон подається формулою:
Геометричний закон розподілу має частота настання події у схемі незалежних повторних випробувань, якщо вони проводяться до першого настання події. У формулі р — імовірність настання події в кожному випробуванні. Геометричний закон розподілу застосовується у задачах статистичного контролю якості і теорії надійності. Числові характеристики розподілу:
_________________________________
46. Розподіл Х2. Розглядаємо послідовність Якщо
Числові характеристики розподілу: M(X)=n. D(X)=2n. _________________________________
Математичне сподівання і дисперсія при нормальному розподілу. Нормальний розподіл — розподіл ймовірностей випадкової величини, що характеризується густиною ймовірності
Нормальний розподіл виникає тоді, коли дана випадкова величина являє собою суму великого числа незалежних випадкових величин, кожна з яких грає в утворенні всієї суми незначну роль. Математичне сподівання нормального розподілу дорівнює параметру а: М(Х) = а.
Дисперсія при нормальному розподілі: D(Х) = σ2. _________________________________
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 275; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.57.54 (0.012 с.) |

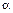 (х) щоразу, коли Х = х, де
(х) щоразу, коли Х = х, де  .
.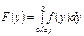 .
.
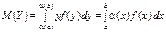 ;
;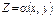 ,
, є невипадковою функцією.
є невипадковою функцією.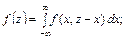
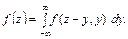
 .
.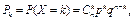
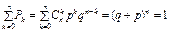 .
.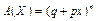 .
.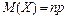 .
.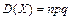 ;
;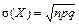 .
. . (1)
. (1) .
.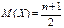 .
.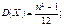
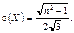
 ,
, dx. (2)
dx. (2) , то маємо:
, то маємо: .
.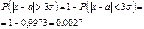
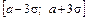 , дорівнює 0,0027.
, дорівнює 0,0027.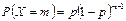
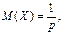
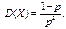
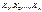 попарно незалежних випадкових величин, які розподілені нормально з нульовими математичними сподіваннями і одиничними дисперсіями.
попарно незалежних випадкових величин, які розподілені нормально з нульовими математичними сподіваннями і одиничними дисперсіями.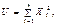 то ця сума має розподіл
то ця сума має розподіл  з
з 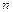 ступенями волі. Щільність розподілу
ступенями волі. Щільність розподілу




