
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поняття випадкового процесу. Прості та складені випадкові події.Содержание книги
Поиск на нашем сайте
Поняття випадкового процесу. Прості та складені випадкові події. Послідовність операцій, виконуваних з додержанням певного комплексу умов, називають експериментом. Наслідок будь-якого експерименту називають подією. Події поділяються на достовірні, неможливі та випадкові. Якщо в результаті випробування деяка подія неодмінно відбудеться, то вона називається достовірною і позначається Ω. Подія, яка в даному випробуванні не може відбутись, називається неможливою і позначається Æ. Якщо в результаті випробування деяка подія може відбутись, а може не відбутись, то вона називається випадковою. Випадкові події позначаються літерами A, B, C, D, …. Для математичного опису випадкових подій застосовують такі точні поняття: прості та складені випадкові події, простір елементарних подій. Подія, що може відбутися внаслідок проведення однієї і лише однієї спроби, називається простою випадковою подією. Елементарні події позначаються wі і не поділяються на простіші складові. Випадкова подія називається складеною, якщо її можна розкласти на прості події. Складені випадкові події позначаються латинськими великими літерами: A, B, C, D, …. Випадковим процесом називається процес, значення якого за будь-якого значення аргументу є випадковою величиною. _________________________________
Операції над подіями. Сумою двох подій А і В називається така подія С = А Добутком двох подій А і В називається така подія С=А Різницею двох подій А і В називається така подія С=А\В (С=А–В), яка внаслідок експерименту настає з настанням події А і одночасним ненастанням події В. Випадкові події А, В, С, для яких визначено операції додавання, множення та віднімання, підлягають таким законам: 1. А 2. А 3. А 4. (А 5. (А 6. (А 7. (А _________________________________ Класичне означення імовірності. Імовірністю випадкової події А називається невід’ємне число Р(А), що дорівнює відношенню числа елементарних подій m (0≤ m ≤ n), які сприяють появі А, до кількості всіх елементарних подій n простору Ω:
Р (А) = Для неможливої події Р (Æ) = 0; Для вірогідної події Р (Ω) = 1. Отже, для довільної випадкової події
_________________________________
Основні формули комбінаторики. Переставленням із n елементів називають такі впорядковані множини з n елементів, які різняться між собою порядком їх розміщення. Кількість таких упорядкованих множин, де всі елементи різні, обчислюється за формулою:
Розміщенням із n елементів по m (0
Комбінаціями з n елементів по
_________________________________
Геометрична ймовірність. Класичне означення ймовірності придатне лише для експериментів з обмеженим числом рівномірних елементарних подій, тобто коли множина W обмежена. Якщо простір елементарних подій W можна подати у вигляді деякого геометричного образу, а множину елементарних подій для події А — як частину цього геометричного образу, то ймовірність події А визначається як відношення мір цих множин:
При цьому вважається, що ймовірність попадання в деяку частину геометричного образу пропорційна до міри цієї його частини. _________________________________
Статистична ймовірність. На практиці обчислити ймовірності випадкових подій можна лише для обмеженого класу задач як для дискретних, так і для неперервних просторів елементарних подій. Для більшості задач, особливо економічних, обчислити ймовірності практично неможливо. У цьому разі використовується статистична ймовірність. Статистичною ймовірністю події А називається відношення кількості m випробувань, в яких подія А відбулась, до загальної кількості виконаних випробувань n: Знаходження статистичної ймовірності пов’язане з проведенням n випробувань, тому вона називається ще частістю, або відносною частотою, події.
Як і для ймовірності випадкової події, для відносної частоти виконується нерівність
Формула повної ймовірності. У разі, коли випадкова подія А може відбутися лише за умови, що відбудеться одна з несумісних випадкових подій Ві, які утворюють повну групу і між собою є попарно несумісними
яка називається формулою повної ймовірності. Випадкові події В1, В2,... Вn називають гіпотезами. _________________________________
Формула Байєса. Застосовуючи формулу множення ймовірностей для залежних випадкових подій А, Ві (і = Р(А) Р(Ві / А) = Р (Ві) Р(А / Ві) → Одержана залежність називається формулою Байєса. Її використовують для переоцінювання ймовірностей гіпотез Ві за умови, що випадкова подія А здійсниться. _________________________________ Формула Бернуллі. Якщо кожний експеримент має лише два несумісні наслідки зі сталими ймовірностями p і q, то їх називають експериментами за схемою Бернуллі. У кожному експерименті випадкова подія з імовірністю p відбувається, а з імовірністю q — не відбувається, тобто p + q = 1. Імовірність того, що в результаті n незалежних експериментів за схемою Бернуллі подія А з’явиться m раз, подається у вигляді
Імовірність того, що в результаті n незалежних експериментів подія А з’явиться від mі до mj раз, обчислюється так:
_________________________________
Локальна теорема Лапласа. Якщо ймовірність появи випадкової події в кожному з n незалежних експериментів є величиною сталою і дорівнює
де називається функцією Гаусса.
_________________________________
Формула Пуассона. При
яка називається формулою Пуассона. Функція Рn (m) визначається за таблицею за заданим m і обчисленим значенням а = np. _________________________________
Математичне сподівання. Однією з найчастіше застосовуваних на практиці характеристик є математичне сподівання. Математичним сподіванням випадкової величини Х, визначеною на дискретному просторі Ω, називається величина
Якщо простір Ω є неперервним, то математичним сподіванням неперервної випадкової величини Х називається величина
Якщо випадкова величина Х Î [а; b], то М (Х) Î [а; b], а саме: математичне сподівання випадкової величини має обов’язково міститься всередині інтервалу [а; b], являючи собою центр розподілу цієї величини. _________________________________
Мода та медіана. Модою (Мo) дискретної випадкової величини Х називають те її можливе значення, якому відповідає найбільша ймовірність появи. Модою для неперервної випадкової величини Х називають те її можливе значення, якому відповідає максимальне значення щільності ймовірності: f (Mо) = max. Якщо випадкова величина має одну моду, то такий розподіл імовірностей називають одномодальним; якщо розподіл має дві моди — двомодальним і т. ін. Існують і такі розподіли, які не мають моди. Їх називають антимодальними. Медіаною (Ме) неперервної випадкової величини Х називають те її значення, для якого виконуються рівність імовірностей подій:
Ме можна знайти, скориставшись щільністю ймовірностей:
або при Х Î [а; b]:
Отже, Ме — можливе значення випадкової величини Х, причому таке, що пряма, проведена перпендикулярно до відповідної точки на площині Х = Ме, поділяє площу фігури, яка обмежена функцією f (x), на дві рівні частини. _________________________________
26. Дисперсія та середньоквадратичне відхилення. Математичне сподівання називають центром розсіювання. Для вимірювання розсіювання вводиться числова характеристика, яку називають дисперсією. Для визначення дисперсії розглядається відхилення випадкової величини Х від свого математичного сподівання (Х – М (Х)) Дисперсією випадкової величини Х називається математичне сподівання квадрата відхилення цієї величини
Для дискретної випадкової величини Х дисперсія
для неперервної
Якщо Х Î [а; b], то Якщо випадкова величина виміряна в деяких одиницях, то дисперсія вимірюватиметься в цих самих одиницях, але в квадраті. Тому доцільно мати числову характеристику такої самої вимірності, як і випадкова величина. Такою числовою характеристикою є середнє квадратичне відхилення. Середнім квадратичним відхиленням випадкової величини Х називають корінь квадратний із дисперсії:
_________________________________ Властивості дисперсії. 1. Якщо С — стала величина, то
Справді
2. Маємо:
3. Якщо А і В — сталі величини, то
Адже
Дисперсію можна обчислити і за такою формулою:
Для дискретної випадкової величини Х
для неперервної
Дисперсія не може бути від’ємною величиною Дисперсія характеризує розсіювання випадкової величини відносно свого математичного сподівання. _________________________________
Асиметрія та ексцес. Третій центральний момент характеризує асиметрію закону розподілу випадкової величини. Якщо m3 = 0, то випадкова величина Х симетрично розподілена відносно М(Х). Оскільки m3 має розмірність випадкової величини в кубі, то вводять безрозмірну величину — коефіцієнт асиметрії:
Центральний момент четвертого порядку використовується для визначення ексцесу, що характеризує плосковершинність, або гостровершинність щільності ймовірності f (x). Ексцес обчислюється за формулою
_________________________________
Біноміальний розподіл. Цілочислова випадкова величина X має біноміальний закон розподілу, якщо ймовірність її можливих значень обчислюється за формулою Бернуллі:
При перевірці виконання умови нормування використовується формула біному Ньютона, тому закон розподілу називають біноміальним:
Імовірнісна твірна функція для біноміального закону
Основні числові характеристики:
_________________________________
Нормальний розподіл. Випадкова величина Х має нормальний закон розподілу ймовірностей, якщо f (х) = де а = М (X), s = s (X). Отже, нормальний закон визначається звідси параметрами а і s і називається загальним. Тоді F(x)=
Для нормального закону Мо=Ме=а. Загальний нормальний закон позначають: N (a; s). _________________________________
Геометричний закон. Закон подається формулою:
Геометричний закон розподілу має частота настання події у схемі незалежних повторних випробувань, якщо вони проводяться до першого настання події. У формулі р — імовірність настання події в кожному випробуванні. Геометричний закон розподілу застосовується у задачах статистичного контролю якості і теорії надійності. Числові характеристики розподілу:
_________________________________
46. Розподіл Х2. Розглядаємо послідовність Якщо
Числові характеристики розподілу: M(X)=n. D(X)=2n. _________________________________
Показовий розподіл. Показовим називають розподіл ймовірності випадкової величини Х, який задається щільністю (а – додатна постійна величина)
Показовий розподіл визначається одним параметром λ. Ця особливість має перевагу в порівнянні з розподілами, що залежать від більшого числа параметрів. Функція розподілу показового закону:
_________________________________
Точкові статистичні оцінки. Статистична оцінка _________________________________
Множинна лінійна регресія На практиці здебільшого залежна змінна У цьому разі регресію називають множинною. При цьому якщо аргументи в функції регресії в першій степені, то множинна регресія називається лінійною, у противному разі — множинною нелінійною регресією. Довірчий інтервал для множинної лінійної регресії Матриця Х містить m лінійно незалежних векторів-стовпців, а це означає, що ранг її дорівнюватиме m і визначник Дисперсії статистичних оцінок Коефіцієнт множинної регресіїТісноту між ознаками Y та X, де
Чим ближче значення R до ±1, тим краще вибрано функцію регресії Нормування коефіцієнтів регресії Множинна лінійна регресія дає змогу порівняти вплив на досліджуваний процес різних чинників. У загальному випадку змінні
де _________________________________ Поняття випадкового процесу. Прості та складені випадкові події. Послідовність операцій, виконуваних з додержанням певного комплексу умов, називають експериментом. Наслідок будь-якого експерименту називають подією. Події поділяються на достовірні, неможливі та випадкові. Якщо в результаті випробування деяка подія неодмінно відбудеться, то вона називається достовірною і позначається Ω. Подія, яка в даному випробуванні не може відбутись, називається неможливою і позначається Æ. Якщо в результаті випробування деяка подія може відбутись, а може не відбутись, то вона називається випадковою. Випадкові події позначаються літерами A, B, C, D, …. Для математичного опису випадкових подій застосовують такі точні поняття: прості та складені випадкові події, простір елементарних подій. Подія, що може відбутися внаслідок проведення однієї і лише однієї спроби, називається простою випадковою подією. Елементарні події позначаються wі і не поділяються на простіші складові. Випадкова подія називається складеною, якщо її можна розкласти на прості події. Складені випадкові події позначаються латинськими великими літерами: A, B, C, D, …. Випадковим процесом називається процес, значення якого за будь-якого значення аргументу є випадковою величиною. _________________________________
Операції над подіями. Сумою двох подій А і В називається така подія С = А Добутком двох подій А і В називається така подія С=А Різницею двох подій А і В називається така подія С=А\В (С=А–В), яка внаслідок експерименту настає з настанням події А і одночасним ненастанням події В. Випадкові події А, В, С, для яких визначено операції додавання, множення та віднімання, підлягають таким законам: 1. А 2. А 3. А 4. (А 5. (А 6. (А 7. (А _________________________________
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 609; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.241.87 (0.013 с.) |

 В (С = А + В), яка внаслідок експерименту настає з настанням принаймні однієї з подій А або В. Операція А
В (С = А + В), яка внаслідок експерименту настає з настанням принаймні однієї з подій А або В. Операція А  В (С=АВ), яка внаслідок експерименту настає з одночасним настанням подій А і В. Операція А
В (С=АВ), яка внаслідок експерименту настає з одночасним настанням подій А і В. Операція А  В називається перерізом цих подій.
В називається перерізом цих подій. А = А, А
А = А, А  А = А.
А = А. .
.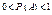 .
. .
. ) називаються такі впорядковані множини, кожна із яких містить m елементів і які відрізняються між собою порядком розташування цих елементів або хоча б одним елементом. Кількість таких множин, де всі елементи різні, обчислюється за формулою:
) називаються такі впорядковані множини, кожна із яких містить m елементів і які відрізняються між собою порядком розташування цих елементів або хоча б одним елементом. Кількість таких множин, де всі елементи різні, обчислюється за формулою: .
. називаються такі множини з m елементів, які різняться між собою хоча б одним елементом. Кількість таких множин:
називаються такі множини з m елементів, які різняться між собою хоча б одним елементом. Кількість таких множин: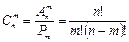 .
. .
.
 .
. _________________________________
_________________________________ , імовірність події А обчислюється за формулою
, імовірність події А обчислюється за формулою ,
,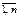 ), дістаємо
), дістаємо

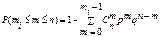 .
.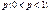 , то для великих значень n і m імовірність того, що випадкова подія А настане m раз, подається такою асимптотичною формулою:
, то для великих значень n і m імовірність того, що випадкова подія А настане m раз, подається такою асимптотичною формулою: ,
,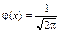 ℮
℮ 
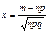 .
.
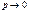 за умови np=a= =const імовірність появи випадкової події m раз
за умови np=a= =const імовірність появи випадкової події m раз 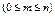 обчислюється за такою асимптотичною формулою:
обчислюється за такою асимптотичною формулою: ,
,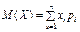

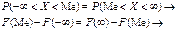

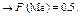
 (2)
(2)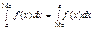 . (3)
. (3)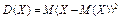 .
.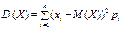 ;
;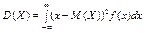 .
.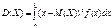 .
.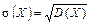 .
.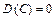 .
.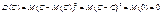 .
. . (2)
. (2)
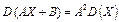 .
.
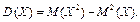
 ;
;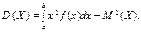
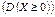 .
.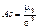 .
.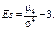
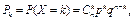
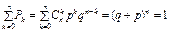 .
.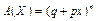 .
.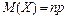 .
.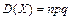 ;
;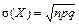 .
. ,
, dx. (2)
dx. (2)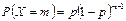
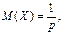
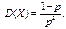
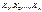 попарно незалежних випадкових величин, які розподілені нормально з нульовими математичними сподіваннями і одиничними дисперсіями.
попарно незалежних випадкових величин, які розподілені нормально з нульовими математичними сподіваннями і одиничними дисперсіями.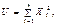 то ця сума має розподіл
то ця сума має розподіл  з
з 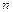 ступенями волі. Щільність розподілу
ступенями волі. Щільність розподілу
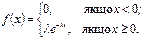
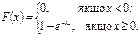
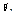 яка визначається одним числом, точкою, називається точковою. Беручи до уваги, що
яка визначається одним числом, точкою, називається точковою. Беручи до уваги, що 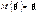 то
то 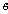 називається незміщеною; в противному разі, тобто коли
називається незміщеною; в противному разі, тобто коли 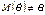 точкова статистична оцінка
точкова статистична оцінка  (3) називається зміщенням статистичної оцінки
(3) називається зміщенням статистичної оцінки  Оцінювальний параметр може мати кілька точкових незміщених статистичних оцінок Точкова статистична оцінка називається ефективною, коли при заданому обсязі вибірки вона має мінімальну дисперсію. Отже, оцінка
Оцінювальний параметр може мати кілька точкових незміщених статистичних оцінок Точкова статистична оцінка називається ефективною, коли при заданому обсязі вибірки вона має мінімальну дисперсію. Отже, оцінка 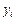 пов’язана з впливом не одного, а кількох аргументів.
пов’язана з впливом не одного, а кількох аргументів.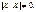 Отже, матриця
Отже, матриця 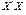 має обернену.
має обернену.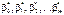 визначають з допомогою кореляційної матриці для вектора
визначають з допомогою кореляційної матриці для вектора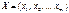 , вимірюють з допомогою коефіцієнта множинної кореляції R, що є узагальненням парного коефіцієнта кореляції rij і обчислюється за формулою
, вимірюють з допомогою коефіцієнта множинної кореляції R, що є узагальненням парного коефіцієнта кореляції rij і обчислюється за формулою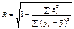 .
. репрезентують чинники, що мають різні одиниці виміру (кілограми, гривні, метри тощо). Отже, для того щоб порівняти і з’ясувати відносну вагомість кожного з чинників, використовують так звані нормовані коефіцієнти регресії, які визначають за формулою
репрезентують чинники, що мають різні одиниці виміру (кілограми, гривні, метри тощо). Отже, для того щоб порівняти і з’ясувати відносну вагомість кожного з чинників, використовують так звані нормовані коефіцієнти регресії, які визначають за формулою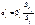

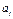 — коефіцієнт регресії після нормування;
— коефіцієнт регресії після нормування; 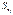 — виправлене середнє квадратичне відхилення змінної
— виправлене середнє квадратичне відхилення змінної 
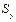 — виправлене середнє квадратичне відхилення ознаки Y.
— виправлене середнє квадратичне відхилення ознаки Y.


