Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Щільність ймовірностей та її властивості.Содержание книги Поиск на нашем сайте
Для неперервних випадкових величин закон розподілу ймовірностей зручно описувати з допомогою щільності ймовірностей, яку позначають f (x). Щільністю ймовірностей неперервної випадкової величини Х називається перша похідна від інтегральної функції F(x):
звідки Властивості f (x) 1. 2. Умова нормування неперервної випадкової величини Х:
3. Імовірність попадання неперервної випадкової величини в інтервалі
4. Функція розподілу ймовірностей неперервної випадкової величини має вигляд
_________________________________
Математичне сподівання. Однією з найчастіше застосовуваних на практиці характеристик є математичне сподівання. Математичним сподіванням випадкової величини Х, визначеною на дискретному просторі Ω, називається величина
Якщо простір Ω є неперервним, то математичним сподіванням неперервної випадкової величини Х називається величина
Якщо випадкова величина Х Î [а; b], то М (Х) Î [а; b], а саме: математичне сподівання випадкової величини має обов’язково міститься всередині інтервалу [а; b], являючи собою центр розподілу цієї величини. _________________________________
Властивості математичного сподівання. 1. Математичне сподівання від сталої величини С дорівнює самій сталій: М (С) = С. 2. М (СХ) = СМ (Х). Для дискретної випадкової величини маємо
Для неперервної:
3. Якщо А і В є сталими величинами, то
_________________________________ Мода та медіана. Модою (Мo) дискретної випадкової величини Х називають те її можливе значення, якому відповідає найбільша ймовірність появи. Модою для неперервної випадкової величини Х називають те її можливе значення, якому відповідає максимальне значення щільності ймовірності: f (Mо) = max. Якщо випадкова величина має одну моду, то такий розподіл імовірностей називають одномодальним; якщо розподіл має дві моди — двомодальним і т. ін. Існують і такі розподіли, які не мають моди. Їх називають антимодальними. Медіаною (Ме) неперервної випадкової величини Х називають те її значення, для якого виконуються рівність імовірностей подій:
Ме можна знайти, скориставшись щільністю ймовірностей:
або при Х Î [а; b]:
Отже, Ме — можливе значення випадкової величини Х, причому таке, що пряма, проведена перпендикулярно до відповідної точки на площині Х = Ме, поділяє площу фігури, яка обмежена функцією f (x), на дві рівні частини.
_________________________________
26. Дисперсія та середньоквадратичне відхилення. Математичне сподівання називають центром розсіювання. Для вимірювання розсіювання вводиться числова характеристика, яку називають дисперсією. Для визначення дисперсії розглядається відхилення випадкової величини Х від свого математичного сподівання (Х – М (Х)) Дисперсією випадкової величини Х називається математичне сподівання квадрата відхилення цієї величини
Для дискретної випадкової величини Х дисперсія
для неперервної
Якщо Х Î [а; b], то Якщо випадкова величина виміряна в деяких одиницях, то дисперсія вимірюватиметься в цих самих одиницях, але в квадраті. Тому доцільно мати числову характеристику такої самої вимірності, як і випадкова величина. Такою числовою характеристикою є середнє квадратичне відхилення. Середнім квадратичним відхиленням випадкової величини Х називають корінь квадратний із дисперсії:
_________________________________ Властивості дисперсії. 1. Якщо С — стала величина, то
Справді
2. Маємо:
3. Якщо А і В — сталі величини, то
Адже
Дисперсію можна обчислити і за такою формулою:
Для дискретної випадкової величини Х
для неперервної
Дисперсія не може бути від’ємною величиною Дисперсія характеризує розсіювання випадкової величини відносно свого математичного сподівання. _________________________________
Початкові та центральні моменти. Початковим моментом k-го порядку випадкової величини Х називають математичне сподівання величини Х k:
Для дискретної випадкової величини Х
для неперервної
Центральним моментом k-го порядку називається математичне сподівання від (Х – М(Х))k:
Для дискретної випадкової величини
для неперервної
_________________________________
Асиметрія та ексцес. Третій центральний момент характеризує асиметрію закону розподілу випадкової величини. Якщо m3 = 0, то випадкова величина Х симетрично розподілена відносно М(Х). Оскільки m3 має розмірність випадкової величини в кубі, то вводять безрозмірну величину — коефіцієнт асиметрії:
Центральний момент четвертого порядку використовується для визначення ексцесу, що характеризує плосковершинність, або гостровершинність щільності ймовірності f (x). Ексцес обчислюється за формулою
_________________________________
|
||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 400; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.177.65 (0.009 с.) |

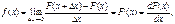

 .
.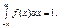
 обчислюється за формулою
обчислюється за формулою
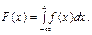
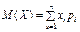

 .
.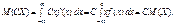
 .
.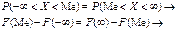

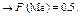
 (2)
(2)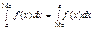 . (3)
. (3)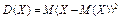 .
.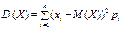 ;
;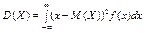 .
.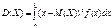 .
.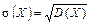 .
.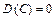 .
.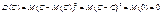 .
. . (2)
. (2)
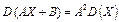 .
.
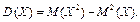
 ;
;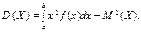
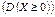 .
. .
. ;
;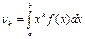 .
.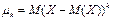 (5)
(5)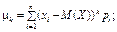
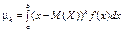 .
.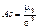 .
.