Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Повторні незалежні випробуванняСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Події називаються повторними, якщо в кожному з них настає одна і та ж подія А з однією і тією ж ймовірністю р. Нехай відносно деякої випадкової події А проводиться n незалежних випробувань. Всі випробування проводяться в однакових умовах, через що ймовірність настання події А залишається однаковою в кожному випробуванні. Ймовірність того, що подія А відбудеться в кожному з незалежних випробувань, позначають Ймовірність однієї складної події, яка полягає в тому, що в n випробуваннях подія А настане m разів і не настане n - m разів дорівнює
Таких складних подій може бути стільки, скільки можна скласти сполучень Формула Бернуллі. Ймовірність того, що в n незалежних випробуваннях, в кожному з яких ймовірність появи події дорівнює р, подія настане m разів (байдуже в якій послідовності), дорівнює:
Формулою (1.17) зручно користуватися, якщо Як наслідок з формули Бернуллі, ймовірність того, що подія настане: а) менше m разів; б) більше m разів; в) не менше m разів; г) не більше m разів; д) від m1 до m2 разів; відповідно дорівнює: а) б) в) г) д) Сума усіх ймовірностей Pn(m) (де m = 0, 1, 2,., n) дорівнює одиниці.
Розв’язання. Маємо схему дев’яти незалежних випробувань. Нехай подія А — «кредит не повернений», тоді 1) 2) Подію «із дев’яти кредитів не більш як з двома виникли проблеми» можна розглядати так:
3) Протилежною для цієї події буде - «усі кредити повернені». Обчислимо цю ймовірність:
Найімовірніше число появи події. Число
Розподіл може мати одне або два найімовірніші числа. Зауваження: Число
Розв’язання. Скористаємося формулою, за якою визначається найімовірніше число:
Задача має два розв’язки: n = 66 i n = 67. Формула Пуассона. Якщо в кожному з n незалежних повторних випробувань
Розв’язання. Якщо подія А = {пачку неправильно укомплектовано}, то її ймовірність р = 0,0004. Розглядається схема незалежних випробувань n =5000, m = 3. Ймовірність події А досить мала, тому задачу розв’яжемо за формулою Пуассона: Виконуючи обчислення, знаходимо: Локальна теорема Лапласа. Ймовірність того, що в n незалежних випробуваннях, у кожному з яких Р (А) = р, подія А відбудеться m раз, подається такою наближеною залежністю:
Локальна теорема Лапласа дає змогу обчислювати ймовірності Функцію Значення
Розв’язання. Подія А = {підприємство регіону має порушення фінансової дисципліни}. За умовою Р (А) = р = 0,9. Проведено n = 400 незалежних перевірок. Розв’яжемо задачу за формулою локальної теореми Лапласа:
Отже, Інтегральна теорема Лапласа. Ймовірність того, що подія А відбудеться від
Функція Ф (х)називається функцією Лапласа. Значення функції Лапласа визначають за Додатком 2. При цьому Ф (х)– непарна функція, тобто Ф (- х) = - Ф (х). При значеннях аргументу х > 5 значення функції Ф (х) = 0,5.
Розв’язання. а)Подія А = {порушення фінансової дисципліни мають не менше 480 підприємств}. Її ймовірність р = 0,5, кількість незалежних випробувань n = 1000. Застосуємо формулу інтегральної теореми Лапласа:
функція Лапласа, а далі виконаємо обчислення:
Значення функції Лапласа беруться з відповідної таблиці (додаток 2). б) Подія В = {порушення фінансової дисципліни мають від 480 до 520 підприємств} Виконаємо допоміжні обчислення:
Питання для самоконтролю
1. У чому суть схеми Бернуллі? Записати формулу Бернуллі. 2. Як визначається ймовірність того, що подія настане: а) менше m разів; б) більше m разів; в) не менше m разів; г) не більше m разів; д) від m1 до m2 разів; в n незалежних випробуваннях, в кожному з яких ймовірність появи події дорівнює р. 3. Як визначити найімовірніше число появи події? 4. Записати формулу Пуассона. Коли вона застосовується? 5. Сформулювати локальну теорему Муавра-Лапласа. 6. Як визначається функція Гауса? 7. Сформулювати інтегральну теорему Муавра-Лапласа. 8. Як визначається функція Лапласа і яких значень вона набуває при х > 5? Завдання 4 4.1. Митниця дає офіційну оцінку того, що 20 % усіх осіб, що повертаються із-за кордону, не декларують весь товар, на який накладається податок. Якщо випадково відібрати 6 осіб, які повертаються з-за кордону, то яка ймовірність того, що не менше трьох з них не задекларує товар, який оподатковується? 4.2. Служба податків визначила, що 50 % всіх особистих декларацій про прибуток містить принаймні одну помилку. Якщо випадково відібрати 10 декларацій, то яка ймовірність того, що 5-7 з них міститимуть принаймні одну помилку? 4.3. Банк видає кредитні картки VISA. Було встановлено, що 40 % усіх рахунків оплачуються повністю за їх допомогою. З попереднього року вибрали навмання 6 рахунків. Яка ймовірність, що 4 з них оплачені за допомогою карток VISA? не більше чотирьох? 4.4. Ймовірність несплати податку для кожного із 150 підприємців дорівнює 0,15. Яка ймовірність того, що податки не сплатять а) 20 підприємців, б) не більше 30 підприємців? 4.5. Унаслідок маркетингових досліджень встановлено, що ймовірність реалізації одиниці продукції дорівнює 0,8. Знайти ймовірність реалізації не менше 75 % із чотирьох одиниць продукції. 4.6. Ймовірність виграшу облігації за весь період позики становить 0,6. Куплено 5 облігацій. Знайти ймовірність такої події: а) виграш випаде принаймні на одну облігацію; б) виграють не більш як дві облігації. 4.7. Підприємство має трьох оптових покупців продукції, для кожного з них ймовірність своєчасного розрахунку з підприємством дорівнює 6/7. Визначити ймовірність своєчасного розрахунку за продукцію: а) усіма покупцями; б) не більше ніж одним покупцем. 4.8. Для забезпечення нормальної роботи банку потрібно, щоб справними було не менше ніж 80 % із наявних 50 комп’ютерів. Яка ймовірність нормальної роботи банку, якщо ймовірність вийти з ладу для кожного з комп’ютерів дорівнює 1/9? 4.9. Ймовірність своєчасної реалізації одиниці продукції дорівнює 0,8. Визначити ймовірність своєчасної реалізації не менше ніж 312 одиниць продукції із 400, що надійшли на реалізацію. 4.10. Встановлено, що під час процесу виробництва ймовірність того, що партія товару матиме дефекти, дорівнює 0,1. Якщо є 10 партій, то яка ймовірність, що дефекти матимуть менше ніж 2 партії? 4.11. Ймовірність несплати податку для кожного із 400 підприємців дорівнює 0,1. Яка ймовірність того, що податки не сплатять не більше 37 підприємців? 4.12. Підприємство має 5 постачальників, ймовірність виконання договору для кожного з них дорівнює 0,7. Визначити ймовірність того, що менше 40 % постачальників виконають договір. 4.13. Ймовірність випуску бракованого виробу дорівнює 0,02. Знайти ймовірність того, що число бракованих виробів буде менше трьох, якщо всього виготовлено 150 виробів. 4.14. Бізнесмен, вивчивши попит ринку на нові автомобілі, вирішив продати пробну партію з дев’яти таких автомашин. Ймовірність отримати високий прибуток за рахунок кожної машини оцінена в 0,8. Яка ймовірність отримати високий прибуток за рахунок продажу не більше двох автомашин? 4.15. Ймовірність виконання договору для одного заводу дорівнює 0,4. Яка ймовірність, що договір виконають принаймні три заводи, якщо в місті їх є 4? 4.16. Ймовірність малому підприємству бути банкротом за певний час дорівнює 0,2. Знайти ймовірність того, що з шести малих підприємств за цей час збережуться: а) два; б) більше двох. 4.17. В середньому для 15% договорів страхова компанія виплачує страхову суму. Визначити ймовірність того, що з десяти договорів у разі настання страхового випадку буде пов'язано з виплатою страхової суми: а) три договори; б) менше двох договорів. 4.18. Передбачається, що 10% нових малих підприємств, що відкриваються, припиняють свою діяльність протягом року. Яка ймовірність того, що з шести малих підприємств не більше двох протягом року припинять свою діяльність? 4.19. Унаслідок маркетингових досліджень встановлено, що ймовірність реалізації одиниці продукції дорівнює 0,75. Знайти ймовірність реалізації не менше 70 і не більше 85 із 100 одиниць продукції. 4.20. До банку відправлено 4000 пакетів грошових знаків. Ймовірність того, що пакет містить недостатнє або надлишкове число грошових знаків, дорівнює 0,0001. Знайти ймовірність того, що при перевірці буде знайдено: а) три помилково укомплектованих пакету; б) не більше трьох пакетів. 4.21. При обстеженні статутних фондів банків визначено, що п'ята частина банків мають статутний фонд більш 100 млн. грн. Знайти ймовірність того, що серед 1800 банків мають статутний фонд понад 100 млн. грн.: а) не менше 300; б) від 300 до 400 включно. 4.22. У страховій компанії є 10 000 клієнтів. Кожний з них, страхуючись від нещасного випадку, вносить 500 грн. Ймовірність нещасного випадку 0,0055, а страхова сума, що виплачується постраждалому, складає 50 000 грн. Яка ймовірність того, що: а) страхова компанія потерпить збиток (виплата хоча б одному); б) виплата страхових сум буде здійснена двом клієнтам? 4.23. Промтоварна база обслуговує 8 магазинів. Заявки на товар на наступний день можуть надходити від кожного магазину з ймовірністю 0,6. Знайти найімовірнішу кількість заявок, які можуть надходити на базу щодня, а також ймовірність надходження такої кількості заявок. 4.24. Частка 2-го сорту деякої масової продукції в середньому становить 20 %. Навмання взято 100 примірників цієї продукції. Яка кількість виробів 2-го сорту в утвореній групі найімовірніша і яка ймовірність того, що в цій групі буде саме така кількість виробів 2-го сорту? 4.25. Ймовірність того, що під час сортування скляний виріб буде розбито, дорівнює 0,002. Знайти ймовірність того, що із 1500 виробів при сортуванні буде розбито 4. 4.26. Частка 1-го сорту в деякій продукції в середньому становить 80 %. Яка ймовірність, що в партії з 100 примірників буде а) 77 примірників 1-го сорту, б) не менш як 75 примірників 1-го сорту? 4.27. Ймовірність виконання договору для однієї фірми дорівнює 0,7. Яка ймовірність, що договір виконають: а) принаймні 7 фірм, якщо в місті їх є 9; б) хоча б одна фірма? 4.28. Завод відправив на базу 1000 доброякісних виробів. За час перебування в дорозі кожний виріб може бути пошкоджено з ймовірністю 0,003. Знайти ймовірність того, що на базу прибудуть не більш 2 пошкоджених виробів. 4.29. Ймовірність підприємству певної галузі бути банкротом за певний час дорівнює 0,15. Знайти ймовірність того, що з 50 малих підприємств за цей час збережуться: а) 9; б) не менше 8. 4.30. При обстеженні статутних фондів банків певного району визначено, що 30% банків мають статутний фонд більш 10 млн. грн. Знайти ймовірність того, що серед 10 банків мають статутний фонд понад 10 млн. грн. не менше 3.
2. ВИПАДКОВІ ВЕЛИЧИНИ
|
|||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 2633; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 а ймовірність настання протилежної події
а ймовірність настання протилежної події 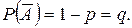

 .
. (1.17)
(1.17) (при великих n розрахунки ускладнюються).
(при великих n розрахунки ускладнюються). ;
; ;
; ;
; ;
;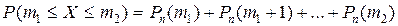 .
.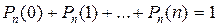
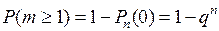
 Ймовірності обчислюватимемо за формулою Бернуллі:
Ймовірності обчислюватимемо за формулою Бернуллі:


 появи події А в n незалежних повторних випробуваннях називається найімовірнішим числом (появи цієї події), якщо їй відповідає найбільша ймовірність. Вона визначається за формулою:
появи події А в n незалежних повторних випробуваннях називається найімовірнішим числом (появи цієї події), якщо їй відповідає найбільша ймовірність. Вона визначається за формулою: (1.18)
(1.18) -це ціле число.
-це ціле число. Підставимо сюди значення відомих величин:
Підставимо сюди значення відомих величин: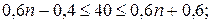



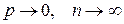 , тоді
, тоді , де
, де  . (1.19)
. (1.19)
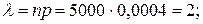
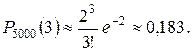
 де
де  ,
, 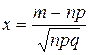 . (1.20)
. (1.20) , якщо n > 10 i p > 0,1.
, якщо n > 10 i p > 0,1. називають функцією ймовірностей або функцією Гауса.
називають функцією ймовірностей або функцією Гауса.
 Підставляючи дані за умовою задачі, дістаємо:
Підставляючи дані за умовою задачі, дістаємо: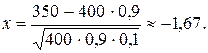 За таблицями (додаток 1) знаходимо
За таблицями (додаток 1) знаходимо  беручи до уваги, що
беручи до уваги, що 
 до
до  раз при проведенні n незалежних випробувань, у кожному з яких подія А відбувається з ймовірністю р, подається формулою:
раз при проведенні n незалежних випробувань, у кожному з яких подія А відбувається з ймовірністю р, подається формулою: ; (1.21)
; (1.21)