
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні правила комбінаторикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Правило суми. Якщо деякий об'єкт х може бути вибраний з сукупності об'єктів
Розв’язання. Три відділення Приватбанку з 8 можна вибрати
Правило добутку. Якщо з деякої кінцевої множини перший об'єкт х можна вибрати
Розв’язання. Три відділення Приватбанку з 8 можна вибрати
Розв’язання. а) Позначимо, Шість акцій із двадцяти можна обрати випадковим чином Три акції із чотирьох банкротів можна обрати випадковим чином Тоді ймовірність події А визначається за формулою (1.1):
б) Позначимо, Одну акцію із чотирьох банкротів можна придбати
Розв’язання. Вибрати 4 листівки 6 видів можна
а) Позначимо, А = {продано 4 однакові листівки}. Число m результатів, що сприяють настанню події А, дорівнює числу
б) Позначимо подію В = {продані 4 різних листівки}. Вибрати 4 листівки з 6 можна Отже,
Питання для самоконтролю
1. Що розуміють під випробуванням, подією? 2. Що називається сумою подій, добутком подій, різницею подій? 3. Які події називаються несумісними? 4. Дати означення повної групи несумісних подій. 5. Які події називаються рівноможливими? 6. Дати означення: а) перестановки з п елементів; б) розміщення з п по m елементів; в) сполучення з п по m елементів. 7. Записати формули для обчислення числа: а) перестановок з п елементів; б) розміщень з п по m елементів; в) сполучень з п по m елементів. 8. Дати означення класичної ймовірності (навести приклади). 9. Сформулювати властивості ймовірності.
Завдання 1 1.1. Керівництво фірми виділило відділу реклами кошти для розміщення у пресі оголошень про товари і послуги, що пропонуються фірмою. За підрахунками відділу реклами виділених коштів вистачить для того, щоб розмістити оголошення лише в 10 з 25 міських газет. Скільки існує способів випадкового відбору газет для розміщення об’яв? Яка ймовірність того, що навмання вибрані 10 редакцій газет виявляться з числа 15 газет, що мають найбільший тираж? 1.2. Нарада директорів складається з 4 бухгалтерів, 3 менеджерів і 2 інженерів. Планується створити підкомітет із трьох його членів. Знайти ймовірність того, що до підкомітету увійдуть бухгалтер і 2 менеджери. 1.3. Скільки існує способів складання у випадковому порядку списку з 7 кандидатів для вибору на керівну посаду? Яка ймовірність того, що кандидати будуть розставлені у переліку за віком (від молодшого до старшого)? 1.4. У двох з 14 складених касиром рахунків є помилки. Ревізор вирішив перевірити навмання 5 рахунків. Яка ймовірність, що помилки не будуть виявлені? 1.5. До ліфта дев’ятиповерхового офісного центру на 1-у поверсі зайшло троє службовців. Кожен із них з однаковою ймовірністю виходить на будь-якому з поверхів, починаючи з 2-го. Знайти ймовірність того, що всі пасажири вийдуть одночасно на одному з поверхів. 1.6. Купуючи картку лотереї «Спортлото», гравець повинен закреслювати 6 з 49 можливих чисел від 1 до 49. Якщо при розіграші лотереї він вгадає всі 6 чисел, то має шанс виграти значну суму грошей. Скільки можливих комбінацій можна скласти з 49 по 6, якщо порядок чисел байдужий? Чому дорівнює ймовірність вгадати всі 6 номерів?
1.7. Магазин отримує товар партіями по 100 штук. Якщо п'ять узятих навмання зразків відповідають стандартам, партія товару поступає на реалізацію. У черговій партії 8 одиниць товару з дефектом. Знайти ймовірність того, що товар поступить на реалізацію. 1.8. Дев'ять запечатаних пакетів з пропозиціями ціни на оренду ділянок для буріння нафтових свердловин поступили вранці в спеціальне агентство ранковою поштою. Скільки існує різних способів черговості відкриття конвертів з пропозиціями ціни? Яка ймовірність того, що конверти випадково виявляться розкритими в залежності від величини пропонованої за оренду ділянок ціни (в порядку зростаючої вартості)? 1.9. На курсах підвищення кваліфікації бухгалтерів навчають визначати правильність оформлення накладної. Для перевірки викладач пропонує перевірити 12 накладних, 5 з яких містять помилки. Навмання вибирають три накладних. Знайти ймовірність того, що з трьох накладних одна з помилками. 1.10. Скільки існує способів складання списку 10 ділових дзвінків випадковим чином? Яка ймовірність того, що список виявиться складеним в алфавітному порядку? Яка ймовірність того, що список з 6 навмання вибраних із 10 запланованих ділових дзвінків виявиться складеним в алфавітному порядку. 1.11. Фірма потребує організації 4 нових складів. Її співробітники підібрали 8 відповідних однаково зручних приміщень, 5 з яких розташовані в багатоповерхових будівлях. Скільки існує способів відбору 4 приміщень з 8 у випадковому порядку? Яка ймовірність того, що всі відібрані приміщення будуть розташовані в багатоповерхових будівлях? 1.12. Із 12 акціонерних товариств 7 успішно функціонують, 3 на межі банкрутства і 2 є банкротами. Громадянин придбав навмання по одній акції 5 акціонерних товариств. Яка ймовірність того, що серед навмання куплених акцій лише одна буде від товариства-банкрота? 1.13. На ринку представлено 8 різних пакетів програм для бухгалтерії з приблизно рівними можливостями, 4 з яких мають найменший об'єм пам'яті. Для апробації в своїх філіалах фірма вирішила відібрати 3 з них. Скільки існує способів відбору 3 програм з 8, якщо відбір здійснений у випадковому порядку? Яка ймовірність того, що випадково відібрані пакети програм займатимуть найменший об'єм пам'яті? 1.14. На пачках грошових банкнот проставлені номери від 1 до 10 за зростаючою сумою грошей у них. Навмання вибираються 4 з них для перерахунку. Знайти ймовірність, що відібрані пачки банкнот будуть: а) з номерами 4, 2, 6, 8; б) будуть розташовані за зростаючою сумою грошей. 1.15. У регіональному відділенні банку операціоністами працює 30 осіб, серед яких 10 чоловіків. Необхідно вибрати делегацію, що складається з 7 співробітників для підвищення кваліфікації і обміну досвідом з іншими відділеннями банку. Знайти ймовірність того, що серед вибраних будуть 3 чоловіки. 1.16. Компанія реалізує 4 види товарів, розташованих на різних складах. Знайти ймовірність, що для реалізації наступних 3 крупних замовлень від різних клієнтів доведеться виїжджати на різні склади. 1.17. Порада директорів складається з 3 бухгалтерів, 3 менеджерів і 2 інженерів. Планується створити підкомітет з трьох його членів. Знайти ймовірність того, що до підкомітету увійдуть два бухгалтери і менеджер.
1.18. Виділені крупні суми на виконання 4 крупних урядових програм, що обіцяють виконавцям високий прибуток. Скільки існує способів випадкового розподілу цих 4 програм між 6 можливими виконавцями? Яка ймовірність того, що кошти на виконання програм при такому розподілі отримають саме 4 виконавця, що мають найбільший прибуток? 1.19. Брокерська фірма пропонує акції різних компаній. Акції 10 з них продаються за найменшою серед наявних акцій ціною і володіють однаковою прибутковістю. Клієнт збирається придбати акції 3 таких компаній — по 1 від кожної компанії. Мається на увазі, що ціни на акції компаній наступного року зміняться і будуть різними. Скільки існує способів вибору 3 таких акцій з 10, якщо вибір здійснюється у випадковому порядку? Яка ймовірність того, що придбані акції попадуть в число акцій, зростання цін на які буде найбільшим наступного року? 1.20. Фірми F1, F2, F3, F4, F5 пропонують свої умови по виконанню 3 різних контрактів К1, К2 і КЗ. Будь-яка фірма може отримати лише один контракт. Контракти різні, тобто якщо фірма F1 отримає контракт К1, то це не те ж саме, якщо вона отримає контракт К2. Скільки способів здобуття контрактів мають фірми? Якщо передбачити рівноможливість отримання контрактів, чому дорівнює ймовірність того, що фірма F3 отримає контракт? 1.21. Набір трицифрового номера виграшної облігації виконують триразовим викиданням з урни одного за одним трьох жетонів із п’яти, пронумерованих цифрами від 1 до 5. Знайти ймовірність того, що вибраний номер містить цифру 3. 1.22. У малому підприємстві працюють 4 жінки та 5 чоловіків. Випадковим способом 2 особи запізнились. Знайти ймовірність, що одна з цих осіб – жінка, а друга чоловік. 1.23. Касир видає заробітну платню за 4 відомостями. Яка ймовірність того, що 3 робітника, що підійшли випадковим чином, отримають заробітну платню за різними відомостями? 1.24. У рекламному агентстві|агенції| є 5 послуг: поліграфія, дизайн, виробництво рекламних відеороликів, трансляція відеороликів на телебаченні та у супермаркетах. У агентство|агенцію| прийшло 4 замовлення. Знайти ймовірність, що всі замовлення на послуги одного виду. 1.25. У філії банку працюють 15 співробітників, 3 з яких не мають потрібної кваліфікації. Яка ймовірність, що два з трьох навмання відібраних для підвищення кваліфікації співробітника не мають потрібної кваліфікації?
1.26. Консультаційній фірмі пропонують 2 замовлення від першої корпорації і 7 від другої. Експерти фірми вважають, що виконати консультаційна фірма може лише 3 з них. Яка ймовірність того, що з 3 навмання вибраних для розгляду замовлень одне замовлення буде від першої, а два від другої корпорацій? 1.27. Із 20 банків 10 розташовані за межами міста. Для дослідження випадково обрано 5 банків. Яка ймовірність того, що серед обраних у межах міста виявляться 3 банки? 1.28. Брокерська фірма пропонує акції 3 різних компаній за найвищою ціною. Клієнт збирається навмання придбати 5 акцій незалежно від аналізу ситуації на ринку. Яка ймовірність того, що всі придбані акції будуть однієї компанії? 1.29. В торговому підприємстві, що займається реалізацією напоїв, працюють 10 менеджерів, 4 з яких мають певний досвід роботи. Підприємству необхідно для розширення сфери торгівлі у літній період відправити у відрядження 3 менеджера з продаж. Яка ймовірність того, що серед навмання відібраних 2 будуть мати певний досвід роботи? 1.30. У центральну бухгалтерію районного відділу освіти поступають звіти від 10 дитячих садків та 15 шкіл. Яка ймовірність того, що з 4 навмання вибраних для перевірки звітів два будуть з дитячих садків?
|
||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 600; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.200.26 (0.014 с.) |

 способами і після кожного такого вибору об'єкт у може бути вибраний
способами і після кожного такого вибору об'єкт у може бути вибраний  способами, то будь-який з даних об'єктів (х або у) може бути вибраний
способами, то будь-який з даних об'єктів (х або у) може бути вибраний  способами.
способами. способами, два відділення Ощадбанку з 9 можна вибрати
способами, два відділення Ощадбанку з 9 можна вибрати 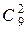 способами. Тоді, згідно правила суми, обмін грошей можна зробити
способами. Тоді, згідно правила суми, обмін грошей можна зробити способами.
способами. способами.
способами. способами.
способами.
 способами.
способами. способами.
способами.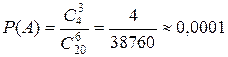

 способами, а дві інших із 16 не банкротів —
способами, а дві інших із 16 не банкротів —  способами. Тоді ймовірність події В відповідно до формули (1.1):
способами. Тоді ймовірність події В відповідно до формули (1.1):
 | = 126 способами, тобто n = 126.
| = 126 способами, тобто n = 126.
 = 15 способами, тобто mB = 15.
= 15 способами, тобто mB = 15. .
.


