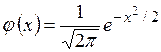Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закони розподілу неперервних випадкових величинСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
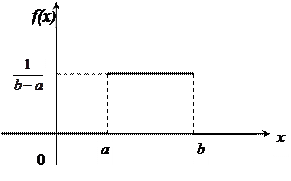
Рівномірний розподіл. Розподіл ймовірностей називається рівномірним, якщо на інтервалі, якому належать можливі значення випадкової величини щільність ймовірностей зберігає стале значення, тобто:
Функція розподілу рівномірного закону має вигляд:
Розв’язання. Щільність ймовірностей випадкової величини х, що має рівномірний розподіл, визначається за формулою: По умові завдання мінімальна ціна товару дорівнює а = 1200 грн., а максимальна b = 1800 грн., і щільність ймовірностей ціни товару х можна записати у вигляді:
Функція розподілу рівномірно розподіленої випадкової величини може бути записана у вигляді:
Ймовірність попадання випадкової величини в деякий інтервал (a,b) визначається формулою
В інтегралі нижня межа узята рівною а = 1200, оскільки при х < а = =1200 f (x)= 0.
Математичне сподівання рівномірно розподіленої випадкової величини визначається за формулою (2.13). Для математичного сподівання ціни товару отримали:
Дисперсію ціни товару знайдемо за формулою (2.13):
Середнє квадратичне відхилення ціни товару від математичного сподівання буде дорівнювати:
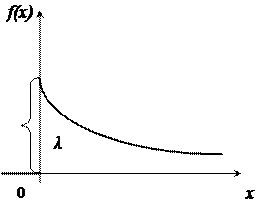
Показниковий розподіл. Показниковим називають розподіл ймовірностей неперервної випадкової величини Х, яку можна описати щільністю
Функція розподілу показникового закону:
Ймовірність попадання значень випадкової величини Х, розподіленої за показниковим законом в інтервал
Розв’язання. За формулами (2.15) маємо:
Нормальний розподіл. Закон розподілу ймовірностей неперервної випадкової величини Х називається нормальним, якщо його щільність має вигляд
де
Ймовірність попадання в заданий інтервал нормально розподіленої випадкової величини
Ймовірність заданого відхилення
Розв’язання. Знайдемо: Тоді
Розв’язання. Скориставшись формулою (2.18), маємо:
За таблицею додатка 2 знайдемо, що отже,
Питання для самоконтролю 1. Описати закони розподілу ймовірностей дискретної випадкової величини (біноміальний, геометричний, гіпергеометричний і закон розподілу Пуассона). Як визначаються їх числові характеристики? 2. Дати означення рівномірного, показникового та нормального розподілів неперервних випадкових величин. 3. Як визначаються числові характеристики 4. Як знайти 5. Якими параметрами визначається нормальний розподіл, який їх імовірнісний зміст? Накреслити криву нормального розподілу. 6. Записати формулу для обчислення ймовірності попадання значень нормально розподіленої випадкової величини в інтервал Завдання 7 7.1. Середнє значення розподілу доходів працівників фірми становить 15 000 грн. і середньоквадратичне відхилення - 2 000 грн. Якщо працівника вибрано навмання, то яка ймовірність того, що він заробляє від 10 000 до 20 000 грн.? 7.2. Державна податкова адміністрація проаналізувала благодійні внески всіх осіб, що зробили їх зі своїх прибутків. Служба встановила, що внески на одного працівника нормально розподіляються із середнім значенням 840 грн. і середнім квадратичним відхиленням 180 грн. Якщо вибрати навмання одного працівника, то яка ймовірність того, що протягом року він вніс менше ніж 435 грн.?
7.3. Статистичні дані прибутку на душу населення показали, що річний прибуток людей міста має нормальний розподіл із середнім значенням 9 000 грн. і середньоквадратичним відхиленням - 1 500 грн. Якщо вибрано певну особу навмання, то яка ймовірність того, що її річний прибуток знаходиться між 8 520 та 12200 грн.? 7.4. Річний прибуток від копіювальних машин має нормальний розподіл, середнє значення якого 720 000 грн. і середньоквадратичне відхилення 80 000 грн. Якщо вибрано копіювальну машину навмання, то яка ймовірність того, що річний прибуток від неї буде від 600 000 до 800 000 грн.? 7.5. Припустимо, що протягом року ціна на акції деякої компанії є випадкова величина, розподілена за нормальним законом з математичним сподіванням 48 у. о., і середнім квадратичним відхиленням 6 у. о. Визначите ймовірність того, що у випадково вибраний день ціна за акцію була більше 60 у. о. 7.6. Банк провів дослідження про наявність річних заощаджень у осіб, вік яких не менше 21 року. Дослідження показали, що річні заощадження на одну особу нормально розподіляються з середнім числом 1 850 грн. і середнім квадратичним відхиленням – 350 грн. Визначити ймовірність того, що навмання вибрана особа має заощадження більше ніж 2 200 грн. 7.7. Середня ціна деякої з великої кількості акцій становить 12 грн. 80 коп., а середнє квадратичне відхилення – 3 грн. Припускаємо, що ціни розподілені за нормальним законом. Знайти яку частку акцій продають за ціною, не вищою від 10 грн.? 7.8. Помилки в обчисленнях, допущені бухгалтером при складанні балансу, розподіляються у відсотках за нормальним законом з параметрами а =1,5 і 7.9. Банк провів дослідження про наявність річних заощаджень у осіб, вік яких не менше 21 року. Дослідження показали, що річні заощадження на одну особу нормально розподіляються з середнім числом 1 850 грн. і середнім квадратичним відхиленням – 350 грн. Визначити ймовірність того, що навмання вибрана особа має заощадження менше ніж 1 500 грн. 7.10. Припустимо, що протягом року ціна на акції деякої компанії є випадкова величина, розподілена за нормальним законом з математичним сподіванням 48 у. о., і середнім квадратичним відхиленням 6 у. о. Визначити ймовірність того, що у випадково вибраний день ціна за акцію була нижча за 60 у. о. 7.11. Державна податкова адміністрація проаналізувала благодійні внески всіх осіб, що зробили їх зі своїх прибутків. Служба встановила, що внески на одного працівника нормально розподіляються із середнім значенням 840 грн. і середнім квадратичним відхиленням 180 грн. Якщо вибрати навмання одного працівника, то яка ймовірність того, що протягом року він вніс від 390 грн. до 1 380 грн.; 7.12. Середній прибуток на душу населення в розмірі 8 000 грн. вважається випадковою величиною, що розподілена нормально із середнім квадратичним відхиленням 7.13. Річний прибуток від копіювальних машин має нормальний розподіл, середнє значення якого 720 000 грн. і середньоквадратичне відхилення 80 000 грн. Якщо вибрано копіювальну машину навмання, то яка ймовірність того, що річний прибуток від неї менш ніж 500 000 грн.?
7.14. Середня ціна деякої великої кількості акцій становить 12 грн. 80 коп., а середнє квадратичне відхилення – 3 грн. Припускаємо, що ціни розподілені за нормальним законом. Знайти ймовірність того, що навмання взята акція матиме ціну від 11 до 14 грн. 7.15. Статистичні дані доходу на душу населення показали, що річний прибуток людей міста має нормальний розподіл із середнім значенням 9 000 грн. і середньоквадратичним відхиленням -1 500 грн. Якщо вибрано певну особу навмання, то яка ймовірність того, що її річний прибуток є більшим ніж 6000 грн.? 7.16. Середнє значення розподілу доходів працівників фірми становить 15 000 грн. і середньоквадратичне відхилення - 2 000 грн. Якщо працівника вибрано навмання, то яка ймовірність того, що він заробляє більше ніж 16 000 грн.? Менше ніж 12 000 грн.? 7.17. Припустимо, що протягом року ціна на акції деякої компанії є випадкова величина, розподілена за нормальним законом з математичним сподіванням 48 у. о., і середнім квадратичним відхиленням 6 у. о. Визначити ймовірність того, що у випадково вибраний день ціна за акцію була вища за 40 у. о. 7.18. Банк провів дослідження про наявність річних заощаджень в осіб, вік яких не менш ніж 21 рік. Дослідження показали, що річні заощадження на одну особу нормально розподіляються з математичним сподіванням 1850 грн. і середнім квадратичним відхиленням – 350 грн. Визначити ймовірність того, що навмання вибрана особа має заощадження у межах від 1080 до 2375 грн. 7.19. Статистичні дані доходу на душу населення показали, що річний прибуток людей міста має нормальний розподіл із середнім значенням 9 000 грн. і середньоквадратичним відхиленням -1 500 грн. Якщо вибрано певну особу навмання, то яка ймовірність того, що її річний прибуток є між 12 400 та 13 000 грн.? 7.20. Річний прибуток від копіювальних машин має нормальний розподіл, середнє значення якого 720 000 грн. і середньоквадратичне відхилення 80 000 грн. Якщо вибрано копіювальну машину навмання, то яка ймовірність того, що річний прибуток від неї перевищує 900 000 грн.? 7.21. Середня ціна деякої великої кількості акцій становить 12 грн. 80 коп., а середнє квадратичне відхилення – 3 грн. Припускаємо, що ціни розподілені за нормальним законом. Знайти нижче від якої ціни продаються 20 % найдешевших акцій? 7.22. Державна податкова адміністрація проаналізувала благодійні внески всіх осіб, що зробили їх зі своїх прибутків. Служба встановила, що внески на одного працівника нормально розподіляються із середнім значенням 840 грн. і середнім квадратичним відхиленням 180 грн. Якщо вибрати навмання одного працівника, то яка ймовірність того, що протягом року він вніс більше ніж 1 020 грн.?
7.23. Статистичні дані прибутку на душу населення показали, що річний прибуток людей міста має нормальний розподіл із середнім значенням 9 000 грн. і середньоквадратичним відхиленням -1 500 грн. Якщо вибрано певну особу навмання, то яка ймовірність того, що її річний прибуток є більшим ніж 10200 грн.? 7.24. За даними досліджень встановлено, що денна середня заробітна плата робітника заводу знаходиться в межах [64-70] грн. і розподілена нормально з параметрами а = 68 грн. і 7.25. Річний прибуток від копіювальних машин має нормальний розподіл, середнє значення якого 720 000 грн. і середньоквадратичне відхилення 80 000 грн. Якщо вибрано копіювальну машину навмання, то яка ймовірність того, що річний прибуток від неї від 540 000 до 660 000 грн.? 7.26. Середній прибуток на душу населення в розмірі 150 грн. вважається випадковою величиною, яка розподілена нормально із середнім квадратичним відхиленням 20 грн. В яких межах практично можна гарантувати прибуток на душу населення з ймовірністю 0,9973? 7.27. Банк провів дослідження про наявність річних заощаджень в осіб, вік яких не менше 21 року. Дослідження показали, що річні заощадження на одну особу нормально розподіляються з середнім числом 1 850 грн. і середнім квадратичним відхиленням – 350 грн. Визначити ймовірність того, що навмання вибрана особа має заощадження менше ніж 800 грн. 7.28. Державна податкова адміністрація проаналізувала благодійні внески всіх осіб, що зробили їх зі своїх прибутків. Служба встановила, що внески на одного працівника нормально розподіляються із середнім значенням 840 грн. і середнім квадратичним відхиленням 180 грн. Якщо вибрати навмання одного працівника, то яка ймовірність того, що протягом року він вніс більше ніж 300 грн.? 7.29. Припустимо, що протягом року ціна на акції деякої компанії є випадкова величина, розподілена за нормальним законом з математичним сподіванням 48 у. о., і середнім квадратичним відхиленням 6 у. о. Визначити ймовірність того, що у випадково вибраний день ціна за акцію була між 40 і 50 у.о. за акцію. 7.30. Один з методів, що дозволяють добитися успішних економічних прогнозів, полягає в застосуванні погоджених підходів до вирішення конкретної проблеми. Зазвичай прогнозом займається велике число аналітиків. Середній результат таких індивідуальних прогнозів є загальним погодженим прогнозом. Цей прогноз відносно величини банківської відсоткової ставки в поточному році підкоряється нормальному закону з середнім значенням а =9% і середнім квадратичним відхиленням 2,6%. З групи аналітиків випадковим чином відбирається одна людина. Визначити ймовірність того, що згідно прогнозу цього аналітика рівень відсоткової ставки буде в межах від 12 до 15%.
Додаток 1 Таблиця значень функції
Додаток 2
Таблиця значень функції Лапласа
Додаток 3 ТАБЛИЦЯ ВИБОРУ ІНДИВІДУАЛЬНИХ ЗАВДАНЬ|задавань|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1246; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.243.136 (0.008 с.) |

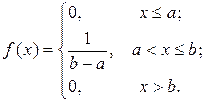
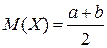 ;
; 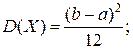
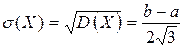 (2.13)
(2.13)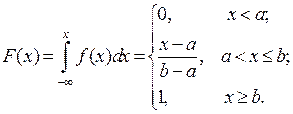


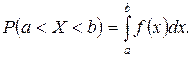
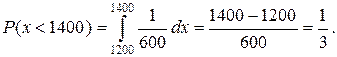
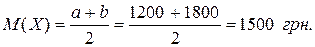
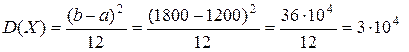 (грн.)2.
(грн.)2.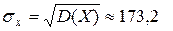 грн.
грн.
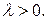
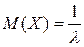 ;
; 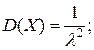
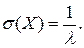 (2.14)
(2.14)
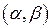 визначається за формулою
визначається за формулою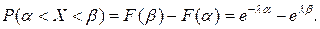 (2.15)
(2.15) . Знайти ймовірність події
. Знайти ймовірність події 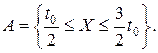
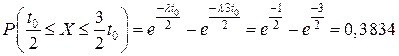


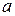 і
і  – параметри розподілу.
– параметри розподілу.
 (2.16)
(2.16) Ф
Ф 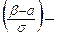 Ф
Ф 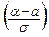 (2.17)
(2.17)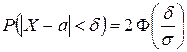 (2.18)
(2.18)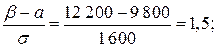
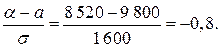
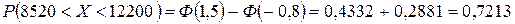 .
. і
і 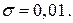 Якими будуть межі помилок обчислень з ймовірністю 0,9973?
Якими будуть межі помилок обчислень з ймовірністю 0,9973?
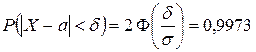 Тоді
Тоді 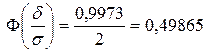 .
.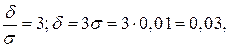
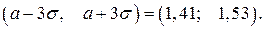
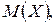
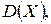
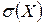 рівномірно розподіленої випадкової величини Х.
рівномірно розподіленої випадкової величини Х.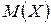 і
і 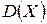 показникового закону, знаючи параметр
показникового закону, знаючи параметр  За якою формулою обчислюється ймовірність попадання значень показниково розподіленої неперервної величини
За якою формулою обчислюється ймовірність попадання значень показниково розподіленої неперервної величини 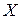 в інтервал
в інтервал 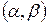 ?
?