
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розподіл Бозе-Ейнштейна та Фермі-ДіракаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
За типом просторової симетрії псі-функції системи квантових частинок поділяються на два види. Системи частинок, які описуються симетричними відносно перестановки координат псі-функціями, мають цілий спін і називаються бозонами, а при антисиметричних із напівцілим спіном - ферміонами. Відповідно до цього, у квантовій статистиці розглядаються дві статистики з функціями розподілу Фермі-Дірака(ферміони) та Бозе-Ейнштейна(бозони). Вони визначають середнє число частинок системи, що мають енергію En при температурі Т і їх можна записати у вигляді
де З визначення (6) випливає, що
де N - число частинок системи, а рівність називається умовою нормування функції розподілу f(En). Вираз (6) можна представити у вигляді
При достатньо високих температурах, коли виконується нерівність
обидві статистики переходять у класичну
Перехід від (6) до (7) має температурну межу, що називається температурою виродження
При Т <
Властивості функції розподілу для металів Функція розподілу електронів у металі має вид
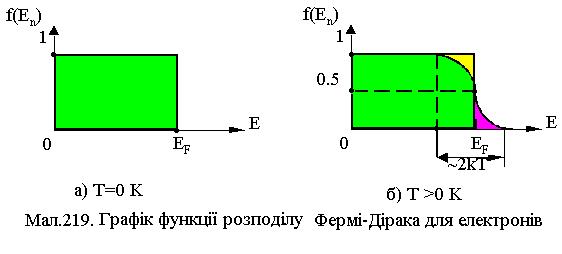
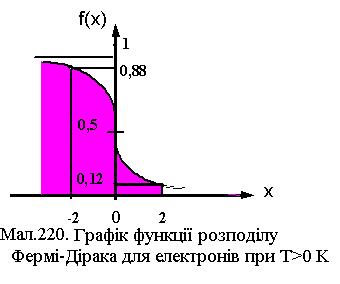
і при температурі  К для електронів з енергією К для електронів з енергією 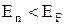 її величина дорівнює 1 (див.Мал.219,а)). При температурі Т > 0 величина f(En) мало змінюється в інтервалі енергій ( її величина дорівнює 1 (див.Мал.219,а)). При температурі Т > 0 величина f(En) мало змінюється в інтервалі енергій (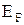 -kT, -kT, 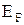 + kT), що для кімнатних температур становить лише 0,025 еВ (див.Мал.219,б)). Дійсно, введемо заміну змінної + kT), що для кімнатних температур становить лише 0,025 еВ (див.Мал.219,б)). Дійсно, введемо заміну змінної  , де х - змінна величина в одиницях kT, що відраховує енергію від , де х - змінна величина в одиницях kT, що відраховує енергію від 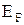 , а , а 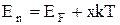 . Тепер функція розподілу f(x) набуває вигляду . Тепер функція розподілу f(x) набуває вигляду  , а таблиця значень функції буде такою , а таблиця значень функції буде такою
Видно, що при зміні x від -2 до 2 значення функції розподілу Фермі - Дірака змінюється від 0,88 до 0,12. Це означає, що найбільша зміна f(E) відбувається в інтервалі енергій від
Теплоємність кристалів Розглянемо застосування квантової статистики на прикладі розгляду теплоємності твердого тіла. Класична теорія теплоємностівиходить із теореми Больцмана про рівнорозподіл енергії за ступенями свободи. Згідно її положень, тверде тіло уявляється однією великою молекулою з 3N ступенями свободи, серед яких 3N-6 коливальних, 3 поступальні та 3 обертові. Так як N>>6, то можна прийняти, що усі ступені свободи є коливальними, причому кожна з них має теплову енергію kT. Повна внутрішня енергія моля такої речовини
Тепер теплоємність моля твердого тіла дорівнює
Цей результат дослідним шляхом установили Дюлонг та Пті і він відомий як правило Дюлонга-Пті: молярна теплоємність хімічно простих речовин у кристалічному стані не залежить від температури та рівна 3R. Насправді це правило виконується лише у випадку високих температур. Для низьких температур теплоємність твердого тіла пропорційна Досить близькі до експерименту значення теплоємності дає теорія теплоємності хімічно простих кристалів Дебая. Його ідея полягає в тому, що найбільший внесок у теплоємність дають теплові коливання вузлів кристалічної решітки з низькими акустичними частотами w, які мають довжини хвиль l, більші за період d. Як і у класичній теорії вважається, що N частинок кристала мають 3N коливальних ступенів свободи. Цим ступеням свободи відповідають 3N узагальнених координат, які можна звести до 3N нормальних координат. Останні описують 3N гармонічних коливань частинок. Такі коливання називають осциляторами. З квантової механіки відомо, що енергія осцилятора має дискретні значення
По аналогії з фотонним газом, кожному з таких акустичних коливань зпівставляється квазічастинка, яку називають фононом. Вони існують лише у межах кристала. Для них виконується закон збереження енергії. Квазіімпульс фонона дорівнює
де Розрахуємо число квантових станів для фононів, що мають імпульс в інтервалі від p до p+dp в об'ємі кристала V. Фазовий простір таких коливань визначається різницею об'ємів сфер імпульсу з радіусами p та р+dp і об'ємом кристала V
Як відомо, мінімальний об'єм комірки фазового простору, що відповідає одному, певному станові системи становить
У цьому виразі коефіцієнт 3 уведено з урахуванням того, що у кристалі можуть одночасно існувати дві поперечні хвилі (зсув кристалу) та одна повздовжня хвиля (стиснення кристалу). З міркувань граничних умов для стоячих хвиль, довжина акустичної хвилі l, породженої коливаннями вузлів кристалічної решітки, не може бути меншою двох періодів кристала - 2d. Такій довжині хвилі відповідає максимальна частота коливань W. Повне число коливань визначається числом ступенів свободи для системи з N частинок, що рівне 3N і це дає можливість обчислити швидкість фононів u через частоту W
Звідси одержимо
і після підстановки у (3), шукане число станів визнвчиться так
Розподіл осциляторів на можливих енергетичних рівнях (2) визначається розподілом Больцмана, а тому середня енергія фононів
Використовуючи (4-5), обчислимо внутрішню енергію Е поля фононів кристала для моля речовини (N=NА) у такий спосіб
або
При високих температурах, коли теплова енергія значно більша енергії фонона kТ >> ħw, в (6) можна покласти
При цьому інтеграл у (6) обчислюється так
В цьому наближенні одержимо
Диференціюючи (7) по Т отримаємо теплоємність, що відповідає правилу Дюлонга-Пті
У випадку, коли енергія фонона більша теплової енергії ħw > kT,
Уведемо у (8) заміну змінної, поклавши
Тепер інтеграл у (8) приводиться до такого вигляду
Величина
Утворення кристалів У процесі кристалізації (перехід речовини з рідини у тверде тіло) із розплаву чи розчину атоми речовини зближуються і між ними виникає сила взаємодії, завдяки якій утворюється стійка кристалічна структура з певними елементами симетрії. З точки зору провідності електричного струму кристали поділяються на провідники, напівпровідники та діелектрики. У провідників атоми зближуються настільки, що валентні (зовнішні) електрони, рухаючись по орбітах, охоплюють сусідні атоми. При тотожності електронів (їх нерозрізнюваності), це явище робить валентні електрони cколективізованими, «вільними»:-вони можуть вільно переміщуватися у межах кристала від одного атома до іншого. Досить прикласти до провідника невелику напругу і в ньому потече електричний струм.
У напівпровідника та діелектрика електронні оболонки валентних (зовнішніх) електронів перекриваються між собою, не охоплюючи сусідні атоми. Таке перекриття створює силовий зв’язок між атомами, а сили взаємодії, які виникають при цьому, носять квантовий характер і називаються обмінними силами. Їх величина залежить від величини перекриття оболонок. При температурі близько 0 К валентні електрони напівпровідників та діелектриків знаходяться при атомах, а енергія, необхідна для відриву валентного електрона від атома, становить 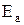 і називається енергією активації. Ця енергія мало змінюється з температурою і практично її можна вважати сталою. У напівпровідників і називається енергією активації. Ця енергія мало змінюється з температурою і практично її можна вважати сталою. У напівпровідників 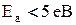 , а у діелектриків , а у діелектриків 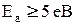 . Такі значення енергії . Такі значення енергії 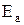 у напівпровідників зумовлюють можливість відриву валентних електронів від атомів за рахунок теплової енергії у напівпровідників зумовлюють можливість відриву валентних електронів від атомів за рахунок теплової енергії 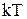 при кімнатних температурах. У діелектриків, при таких температурах, теплової енергії, для утворення достатньої концентрації вільних електронів замало і вони практично не проводять електричний струм при напрузі меншій ніж напруга іонізації. при кімнатних температурах. У діелектриків, при таких температурах, теплової енергії, для утворення достатньої концентрації вільних електронів замало і вони практично не проводять електричний струм при напрузі меншій ніж напруга іонізації.
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 631; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.156.26 (0.01 с.) |

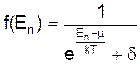 , (6)
, (6) для ферміонів,
для ферміонів, 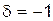 для бозонів. Величина m називається хімічним потенціалом. Вона визначається величиною зміни внутрішньої енергії системи при зміні числа її частинок на одиницю. У випадку ферміонів, якими є електрони у металі, m дорівнює енергії Фермі
для бозонів. Величина m називається хімічним потенціалом. Вона визначається величиною зміни внутрішньої енергії системи при зміні числа її частинок на одиницю. У випадку ферміонів, якими є електрони у металі, m дорівнює енергії Фермі  енергії найвищого заповненого енергетичного рівня. Для фотонів та фононів
енергії найвищого заповненого енергетичного рівня. Для фотонів та фононів  ,
, .
. ,
, . (7)
. (7) системи
системи . (8)
. (8) . Якщо концентрація n електронів у металі складає
. Якщо концентрація n електронів у металі складає  , то у напівпровіднику носії струму мають
, то у напівпровіднику носії струму мають  . Таким чином температура виродження
. Таким чином температура виродження  для напівпровідника складає
для напівпровідника складає  , тобто електронний газ у напівпровідниках завжди невироджений.
, тобто електронний газ у напівпровідниках завжди невироджений.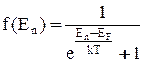
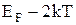 до
до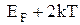 . Для
. Для 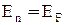 , f(
, f(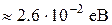 .
.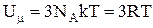 . При нагріванні кристала теплота іде на приріст внутрішньої енергії
. При нагріванні кристала теплота іде на приріст внутрішньої енергії 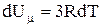 та на роботу по тепловому розширенню
та на роботу по тепловому розширенню 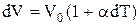 . Звертаючи увагу на те, що теплове розширення твердого тіла незначне (коефіцієнт температурного розширення
. Звертаючи увагу на те, що теплове розширення твердого тіла незначне (коефіцієнт температурного розширення  ), можна знехтувати роботою на розширення і вважати, що молярні теплоємності кристала при сталому тискові
), можна знехтувати роботою на розширення і вважати, що молярні теплоємності кристала при сталому тискові 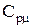 та при сталому об’ємові
та при сталому об’ємові 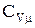 рівні за величиною
рівні за величиною  і
і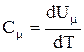
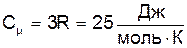 . (1)
. (1)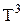 і цей результат має лише квантово-механічне обґрунтування, тобто тверде тіло при низьких температурах необхідно розглядати як квантову систему.
і цей результат має лише квантово-механічне обґрунтування, тобто тверде тіло при низьких температурах необхідно розглядати як квантову систему.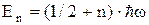 , (n=0,1,2,3....). (2)
, (n=0,1,2,3....). (2)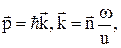
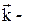 хвильовий вектор, u - швидкість розповсюдження акустичної хвилі в напрямку
хвильовий вектор, u - швидкість розповсюдження акустичної хвилі в напрямку 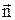 , w - частота коливання осцилятора. При взаємодії фононів закон збереження імпульсу не виконується: імпульс взаємодіючих фононів може передаватися кристалічній решітці. Уведення фононів є зручним методом опису взаємодії акустичних коливань у кристалах.
, w - частота коливання осцилятора. При взаємодії фононів закон збереження імпульсу не виконується: імпульс взаємодіючих фононів може передаватися кристалічній решітці. Уведення фононів є зручним методом опису взаємодії акустичних коливань у кристалах. .
.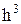 , тому число станів dГ в об'ємі dФ буде дорівнювати
, тому число станів dГ в об'ємі dФ буде дорівнювати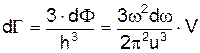 . (3)
. (3)
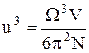
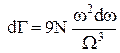 (4)
(4) на частоті w обчислюється так як і у випадку фотонів (формула Планка)
на частоті w обчислюється так як і у випадку фотонів (формула Планка)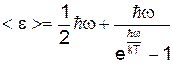 . (5)
. (5)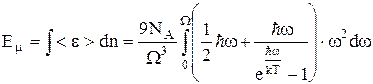
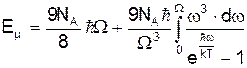 , (6)
, (6) .
.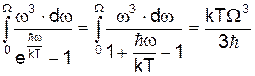 .
. (7)
(7)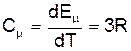 .
.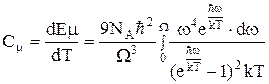 . (8)
. (8) . (9)
. (9)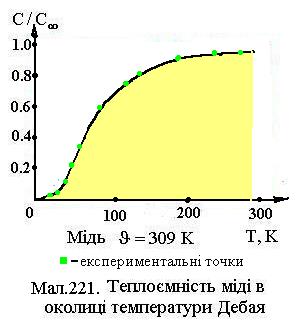
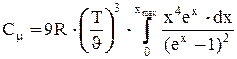 . (10)
. (10)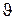 носить назву характеристичної температури Дебаяі визначає граничну температуру кристала, нижче якої теплоємність потрібно визначати на основі квантування акустичного поля. У випадку низьких температур, коли
носить назву характеристичної температури Дебаяі визначає граничну температуру кристала, нижче якої теплоємність потрібно визначати на основі квантування акустичного поля. У випадку низьких температур, коли 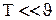 верхня границя інтеграла в (10)
верхня границя інтеграла в (10) 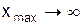 , а сам інтеграл буде деяким числом. При цьому теплоємність буде пропорційна Т3, що відповідає даним експерименту (див.Мал.221). Досліди показують, що одержана залежність теплоємності від температури добре виконується для багатьох хімічно простих речовин, а саме співвідношення відоме, як закон Дебая.
, а сам інтеграл буде деяким числом. При цьому теплоємність буде пропорційна Т3, що відповідає даним експерименту (див.Мал.221). Досліди показують, що одержана залежність теплоємності від температури добре виконується для багатьох хімічно простих речовин, а саме співвідношення відоме, як закон Дебая.



