
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Елементи квантової статистики та фізики твердого тілаСодержание книги
Поиск на нашем сайте
Елементи квантової статистики та фізики твердого тіла Статистичні методи у квантовій механіці Як відомо, із квантової механіки, динаміку елементарних частинок, які знаходяться у силовому потенціальному полі, визначають за допомогою y-функцій Шредінгера. Фізичний зміст цих функцій полягає у тому, що перебування частинки у певному стані задається ймовірністю, густина якої дорівнює квадратові модуля y-функції. Можна ввести 6-вимірний простір із 3-х просторових координат x,y,z та 3-х проекцій імпульсу dW = f (q, p) dФ. (1) У (1) через q та р умовно позначені просторові координати та проекції імпульсу відповідно, dF = dpdq - елемент об'єму фазового простору, а
Функція f(p,q) - густина ймовірності того, що частинка знаходиться в одиничному фазовому об'ємі з координатами q та р. Фазовий простір системи з n частинок є 6n-вимірним. Кожна точка фазового простору повинна була б відповідати одному визначеному станові, як це є у класичній фізиці, але у квантовій механіці де координати та імпульс мають невизначеність за Гейзенбергом
стану частинки відповідає деякий фазовий об'єм dФ=dqdp. Виходячи з (2) можна визначити мінімальний фазовий об'єм, що відповідає одному станові частинки
Якщо деяка функція координат та імпульсу F(p,q) визначена на фазовому просторі системи частинок, то її середнє значення
В (3) інтегрування проводиться по усьому фазовому об'єму системи Ф. Уведення фазового простору (q,p) та густини розподілу f(q,p) є одним із методів опису динаміки системи елементарних частинок через неперервні змінні q та p. Існують також інші методи опису динаміки стану елементарних частинок. Один із них ґрунтується на визначенні стану системи через дискретну змінну величину, якою може бути, наприклад, енергія системи. У цьому випадку функція розподілу f(q,p) визначається на множині дискретних значень енергії Еn, де n - сукупність усіх дискретних квантових чисел, що визначають стан системи. У найбільш загальному вигляді функцію розподілу запропонував Гібсс
Стала А визначається з умови нормування
Властивості функції розподілу для металів Функція розподілу електронів у металі має вид
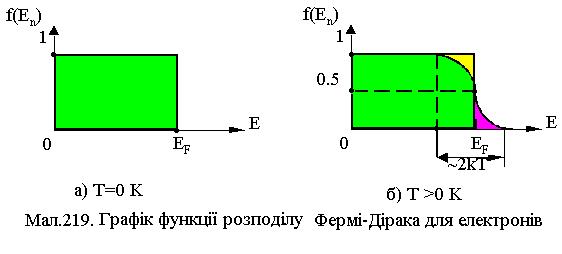
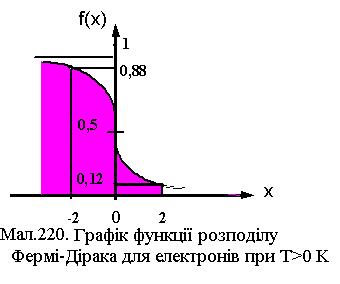
і при температурі  К для електронів з енергією К для електронів з енергією 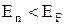 її величина дорівнює 1 (див.Мал.219,а)). При температурі Т > 0 величина f(En) мало змінюється в інтервалі енергій ( її величина дорівнює 1 (див.Мал.219,а)). При температурі Т > 0 величина f(En) мало змінюється в інтервалі енергій (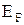 -kT, -kT, 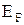 + kT), що для кімнатних температур становить лише 0,025 еВ (див.Мал.219,б)). Дійсно, введемо заміну змінної + kT), що для кімнатних температур становить лише 0,025 еВ (див.Мал.219,б)). Дійсно, введемо заміну змінної  , де х - змінна величина в одиницях kT, що відраховує енергію від , де х - змінна величина в одиницях kT, що відраховує енергію від 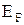 , а , а 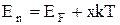 . Тепер функція розподілу f(x) набуває вигляду . Тепер функція розподілу f(x) набуває вигляду  , а таблиця значень функції буде такою , а таблиця значень функції буде такою
Видно, що при зміні x від -2 до 2 значення функції розподілу Фермі - Дірака змінюється від 0,88 до 0,12. Це означає, що найбільша зміна f(E) відбувається в інтервалі енергій від
Теплоємність кристалів Розглянемо застосування квантової статистики на прикладі розгляду теплоємності твердого тіла. Класична теорія теплоємностівиходить із теореми Больцмана про рівнорозподіл енергії за ступенями свободи. Згідно її положень, тверде тіло уявляється однією великою молекулою з 3N ступенями свободи, серед яких 3N-6 коливальних, 3 поступальні та 3 обертові. Так як N>>6, то можна прийняти, що усі ступені свободи є коливальними, причому кожна з них має теплову енергію kT. Повна внутрішня енергія моля такої речовини
Тепер теплоємність моля твердого тіла дорівнює
Цей результат дослідним шляхом установили Дюлонг та Пті і він відомий як правило Дюлонга-Пті: молярна теплоємність хімічно простих речовин у кристалічному стані не залежить від температури та рівна 3R. Насправді це правило виконується лише у випадку високих температур. Для низьких температур теплоємність твердого тіла пропорційна Досить близькі до експерименту значення теплоємності дає теорія теплоємності хімічно простих кристалів Дебая. Його ідея полягає в тому, що найбільший внесок у теплоємність дають теплові коливання вузлів кристалічної решітки з низькими акустичними частотами w, які мають довжини хвиль l, більші за період d. Як і у класичній теорії вважається, що N частинок кристала мають 3N коливальних ступенів свободи. Цим ступеням свободи відповідають 3N узагальнених координат, які можна звести до 3N нормальних координат. Останні описують 3N гармонічних коливань частинок. Такі коливання називають осциляторами. З квантової механіки відомо, що енергія осцилятора має дискретні значення
По аналогії з фотонним газом, кожному з таких акустичних коливань зпівставляється квазічастинка, яку називають фононом. Вони існують лише у межах кристала. Для них виконується закон збереження енергії. Квазіімпульс фонона дорівнює
де Розрахуємо число квантових станів для фононів, що мають імпульс в інтервалі від p до p+dp в об'ємі кристала V. Фазовий простір таких коливань визначається різницею об'ємів сфер імпульсу з радіусами p та р+dp і об'ємом кристала V
Як відомо, мінімальний об'єм комірки фазового простору, що відповідає одному, певному станові системи становить
У цьому виразі коефіцієнт 3 уведено з урахуванням того, що у кристалі можуть одночасно існувати дві поперечні хвилі (зсув кристалу) та одна повздовжня хвиля (стиснення кристалу). З міркувань граничних умов для стоячих хвиль, довжина акустичної хвилі l, породженої коливаннями вузлів кристалічної решітки, не може бути меншою двох періодів кристала - 2d. Такій довжині хвилі відповідає максимальна частота коливань W. Повне число коливань визначається числом ступенів свободи для системи з N частинок, що рівне 3N і це дає можливість обчислити швидкість фононів u через частоту W
Звідси одержимо
і після підстановки у (3), шукане число станів визнвчиться так
Розподіл осциляторів на можливих енергетичних рівнях (2) визначається розподілом Больцмана, а тому середня енергія фононів
Використовуючи (4-5), обчислимо внутрішню енергію Е поля фононів кристала для моля речовини (N=NА) у такий спосіб
або
При високих температурах, коли теплова енергія значно більша енергії фонона kТ >> ħw, в (6) можна покласти
При цьому інтеграл у (6) обчислюється так
В цьому наближенні одержимо
Диференціюючи (7) по Т отримаємо теплоємність, що відповідає правилу Дюлонга-Пті
У випадку, коли енергія фонона більша теплової енергії ħw > kT,
Уведемо у (8) заміну змінної, поклавши
Тепер інтеграл у (8) приводиться до такого вигляду
Величина
Утворення кристалів У процесі кристалізації (перехід речовини з рідини у тверде тіло) із розплаву чи розчину атоми речовини зближуються і між ними виникає сила взаємодії, завдяки якій утворюється стійка кристалічна структура з певними елементами симетрії. З точки зору провідності електричного струму кристали поділяються на провідники, напівпровідники та діелектрики. У провідників атоми зближуються настільки, що валентні (зовнішні) електрони, рухаючись по орбітах, охоплюють сусідні атоми. При тотожності електронів (їх нерозрізнюваності), це явище робить валентні електрони cколективізованими, «вільними»:-вони можуть вільно переміщуватися у межах кристала від одного атома до іншого. Досить прикласти до провідника невелику напругу і в ньому потече електричний струм.
У напівпровідника та діелектрика електронні оболонки валентних (зовнішніх) електронів перекриваються між собою, не охоплюючи сусідні атоми. Таке перекриття створює силовий зв’язок між атомами, а сили взаємодії, які виникають при цьому, носять квантовий характер і називаються обмінними силами. Їх величина залежить від величини перекриття оболонок. При температурі близько 0 К валентні електрони напівпровідників та діелектриків знаходяться при атомах, а енергія, необхідна для відриву валентного електрона від атома, становить 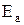 і називається енергією активації. Ця енергія мало змінюється з температурою і практично її можна вважати сталою. У напівпровідників і називається енергією активації. Ця енергія мало змінюється з температурою і практично її можна вважати сталою. У напівпровідників 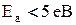 , а у діелектриків , а у діелектриків 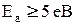 . Такі значення енергії . Такі значення енергії 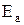 у напівпровідників зумовлюють можливість відриву валентних електронів від атомів за рахунок теплової енергії у напівпровідників зумовлюють можливість відриву валентних електронів від атомів за рахунок теплової енергії 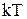 при кімнатних температурах. У діелектриків, при таких температурах, теплової енергії, для утворення достатньої концентрації вільних електронів замало і вони практично не проводять електричний струм при напрузі меншій ніж напруга іонізації. при кімнатних температурах. У діелектриків, при таких температурах, теплової енергії, для утворення достатньої концентрації вільних електронів замало і вони практично не проводять електричний струм при напрузі меншій ніж напруга іонізації.
Електропровідність металів а). Рівняння динаміки руху електронів. Метод ефективної маси Для дослідження руху електронів у періодичному полі кристала достатньо записати та розв'язати рівняння другого закону Ньютона
де m-класична маса електрона,
і може бути визначена через його енергію
Під дією зовнішньої сили
Величину прискорення електрона можна визначити з (3) таким чином
Враховуючи (4), маємо
Вираз (6) можна представити у вигляді рівняння другого закону Ньютона для електрона
де
так звана ефективна маса електрона. Цю масу можна тлумачити як міру інертності електрона до дії зовнішньої сили Знаючи залежність Е від k, можна визначити
У точках перегину кривої (точка В) друга похідна від Е(k)
Це означає, що електрони, які знаходяться посередині енергетичної зони, беруть обмежену участь в електропровідності. На верхніх енергетичних рівнях, під стелею першої зони Брилюєна (точка С), Е має максимум:
Це означає, що під дією сили б). Квантова теорія електропровідності металів
Як показують квантово-механічні розрахунки величина провідності s металів з уведенням ефективної маси
де n- концентрація вільних електронів із зарядом e, t - час релаксації (фактично час вільного пробігу). Щодо температурної залежності s, то до Т=50 К вона Зазначимо, що опір направленому рухові електронів під дією зовнішнього електричного поля пов'язаний з розсіюванням їх на тепловому коливальному русі вузлів кристалічної решітки (фононах) та її дефектах, домішках, вакансіях і механічних неоднорідностях. Контактні явища у металах а). Робота виходу. Метал являє собою кристалічну решітку. При утворенні кристала атоми зближаються на такі відстані, що відбувається перекриття зовнішніх (валентних) та внутрішніх електронних орбіталей. При цьому перекриття валентних орбіталей настільки значне, що валентні електрони одного атома охоплюють сусідні атоми і таким чином вони сколективізуються у газ ‘вільних’ електронів: кожен із них належить усім атомам одночасно і вони можуть вільно переміщуватися в межах кристала. У вузлах кристалічної решітки розміщуються іонізовані таким чином атоми, які знаходяться у тепловому коливальному русі. Вільні електрони можуть рухатися у періодичному полі кристала під дією зовнішнього електричного поля, створюючи електричний струм. Вільні електрони мають ще назву електронів провідності. При Т> 0 К, за рахунок теплової енергії кТ (кінетична енергія), вільні електрони мають можливість виходити за поверхню кристала і повертатися у кристал за рахунок кулонівських сил тяжіння до іонів. При цьому кінетична енергія електрона переходить у потенціальну енергію кулонівської взаїмодії і навпаки. За деякий час установлюється динамічна рівновага між кількістю електронів, що вийшли за поверхню кристала, і кількістю електронів, що повернулися у кристал. Така рівновага підтримує над поверхнею кристала електронну хмарку із середнім зарядом
де  поверхнева різниця потенціалів. поверхнева різниця потенціалів.
б). Закони Вольтадля контактної різниці потенціалів. Для сполучених провідників Вольт установив такі закони: 1. При сполученні двох провідників, виготовлених із різнорідних металів, між точками поблизу їх поверхонь (точки В і С) виникає зовнішня контактна різниця потенціалів, величина якої залежить виключно від їх хімічної природи та температури.
Першопричиною виникнення контактної різниці потенціалів є власні неоднакові роботи виходу металів. При з’єднанні таких провідників у місці контакту відбуваються переходи частини електронів із металу з меншою роботою виходу
Різниця потенціалів (1) називається зовнішньою контактною різницею потенціалів. Вона створює між вільними кінцями провідників електричне поле напруженістю Крім того, різні метали мають різні концентрації nі, а тому і різні енергії Фермі. При При утворенні контакту двох металів з різними концентраціями вільних електронів, через їх границю починається дифузія електронів. Через деякий час концентрації електронів при границі вирівняються а метали будуть мати потенціали
де
Внутрішня контактна різниця потенціалів тепер запишеться так
Відношення сталих
а тому можна записати
За порядком величини
З квантової точки зору, переміщення електронів у прошарку контакту змінює положення рівнів Фермі
При Т=0 К енергія Фермі має вид
а підстановка цього виразу у (3) дає
При Т
З останнього виразу видно, що внутрішня контактна різниця потенціалів залежить від температури квадратично, але залишається досить малою величиною.
Потрібно зауважити, що у зоні контакту шириною 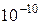 м метали, внаслідок дифузії електронів, заряджуються різнойменно. Однак це не створює потенціального бар’єру для проходження струму у зоні контакту, як це є у напівпровіднику, тому що концентрація вільних електронів практично не змінюється. м метали, внаслідок дифузії електронів, заряджуються різнойменно. Однак це не створює потенціального бар’єру для проходження струму у зоні контакту, як це є у напівпровіднику, тому що концентрація вільних електронів практично не змінюється.
Вираз (1) дає пояснення суті першого закону Вольта, а для пояснення другого закону розглянемо потенціали на границях металів, з'єднаних у ланцюг, як це представлено на Мал.237. Різницю потенціалів між крайніми металами при їх поверхнях (точки В і С) можна записати у вигляді
і тепер
Термоелектрорушійна сила У 1821 році Зеебек виявив, що у замкненому колі з двох різнорідних провідників, контакти яких знаходяться при різних температурах (див. Мал.238) виникає електрорушійна сила, яку назвали термоелектрорушійною- ТЕРС. Основними процесами, що створюють ТЕРС, є такі: 1. Дифузія електронів. В околиці контакту з більшою (меншою) температурою виникають електрони з енергіями більшими (меншими) ніж енергія Фермі. Це створює градієнт концентрації і потік гарячих електронів у напрямку холодного контакту (потік холодних електронів у напрямку гарячого контакту). 2. Зміна рівнів Фермі від температури. Внутрішня контактна різниця потенціалів, що визначається рівнями Фермі, різна у гарячого й холодного контактів і їх різниця, що не дорівнює нулю, як це було б при однакових температурах, дає відповідний вклад у ТЕРС. 3. Утягування електронів потоком фононів. Теплові коливання кристалічної решітки більш інтенсивні біля гарячого контакту, що створює потік фононів у напрямку холодного контакту. Останні, взаємодіючи з електронами, надають їм відповідного направленого руху. Відбувається накопичення електронів біля холодного і збіднення їх біля гарячого контакту.
Розрахунки показують, що величина термоелектрорушійної сили
і за формулою (5) можна записати
Величина a- коефіцієнт термоелектрорушійної сили, характерний для кожної з пар металів. Цей класичний результат збігається з квантово-механічним для малих різниць температур спаїв Коефіцієнт корисної дії (ККД) термопар із металів складає ~ 0.1% у той час як термопари з напівпровідників мають ККД ~ 15% і у принципі може бути підвищеним. Проте цей ефект знайшов широке застосування у приладах, що вимірюють температуру.
Напівпровідниковий діод
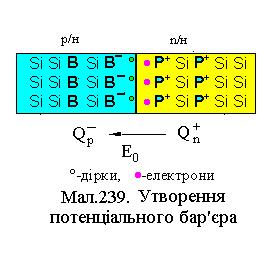 При утворенні контакту р- та n-напівпровідників через нього виникає дифузія та рекомбінація носіїв струму в обох областях. Дифузія виникає внаслідок різної концентрації електронів та дірок у сполучених р- та n-областях. При дифузії вільного електрона з n-області там залишається додатній іон донорної домішки При утворенні контакту р- та n-напівпровідників через нього виникає дифузія та рекомбінація носіїв струму в обох областях. Дифузія виникає внаслідок різної концентрації електронів та дірок у сполучених р- та n-областях. При дифузії вільного електрона з n-області там залишається додатній іон донорної домішки 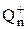 (від нього саме відірвався цей електрон) і в р-області він займає вакансію зв’язку акцепторної домішки, перетворюючи її у від’ємний іон (від нього саме відірвався цей електрон) і в р-області він займає вакансію зв’язку акцепторної домішки, перетворюючи її у від’ємний іон 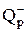 . Такий процес називається рекомбінацією електрона та дірки. Слід окремо зауважити, що під час рекомбінації у контактному прошарку зникають носії струму. Під рекомбінацією дірки у n-області слід розуміти виникнення вакансії зв'язку між атомами у ній і зайняття її електроном донора. Це означає зникнення електрона й дірки, як носіїв струму, й утворення знову ж таки додатного іона донорної домішки в n-області й від’ємного іона акцепторної домішки в p-області. . Такий процес називається рекомбінацією електрона та дірки. Слід окремо зауважити, що під час рекомбінації у контактному прошарку зникають носії струму. Під рекомбінацією дірки у n-області слід розуміти виникнення вакансії зв'язку між атомами у ній і зайняття її електроном донора. Це означає зникнення електрона й дірки, як носіїв струму, й утворення знову ж таки додатного іона донорної домішки в n-області й від’ємного іона акцепторної домішки в p-області.
Таким чином, границя n- і р-області збіднюється носіями струму, а зарядами іонів домішок створюється внутрішнє електричне поле з напруженістю При накладанні зовнішнього поля з напруженістю Відношення
Елементи квантової статистики та фізики твердого тіла
|
|||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 313; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.42.59 (0.016 с.) |

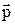 на них - pх,pу,pz, який називається фазовим. Кожній точці цього простору відповідає певний стан частинки. Імовірність стану визначається виразом
на них - pх,pу,pz, який називається фазовим. Кожній точці цього простору відповідає певний стан частинки. Імовірність стану визначається виразом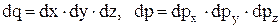 .
.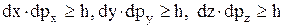 (2)
(2)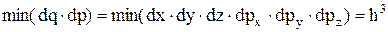 .
. обчислюється за правилом:
обчислюється за правилом: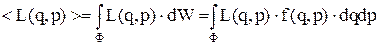 (3)
(3)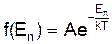 . (4)
. (4) . (5)
. (5)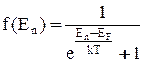
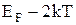 до
до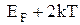 . Для
. Для 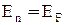 , f(
, f(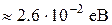 .
.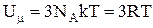 . При нагріванні кристала теплота іде на приріст внутрішньої енергії
. При нагріванні кристала теплота іде на приріст внутрішньої енергії 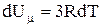 та на роботу по тепловому розширенню
та на роботу по тепловому розширенню 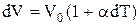 . Звертаючи увагу на те, що теплове розширення твердого тіла незначне (коефіцієнт температурного розширення
. Звертаючи увагу на те, що теплове розширення твердого тіла незначне (коефіцієнт температурного розширення  ), можна знехтувати роботою на розширення і вважати, що молярні теплоємності кристала при сталому тискові
), можна знехтувати роботою на розширення і вважати, що молярні теплоємності кристала при сталому тискові 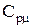 та при сталому об’ємові
та при сталому об’ємові 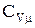 рівні за величиною
рівні за величиною  і
і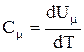
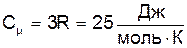 . (1)
. (1)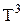 і цей результат має лише квантово-механічне обґрунтування, тобто тверде тіло при низьких температурах необхідно розглядати як квантову систему.
і цей результат має лише квантово-механічне обґрунтування, тобто тверде тіло при низьких температурах необхідно розглядати як квантову систему.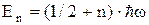 , (n=0,1,2,3....). (2)
, (n=0,1,2,3....). (2)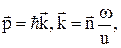
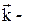 хвильовий вектор, u - швидкість розповсюдження акустичної хвилі в напрямку
хвильовий вектор, u - швидкість розповсюдження акустичної хвилі в напрямку 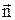 , w - частота коливання осцилятора. При взаємодії фононів закон збереження імпульсу не виконується: імпульс взаємодіючих фононів може передаватися кристалічній решітці. Уведення фононів є зручним методом опису взаємодії акустичних коливань у кристалах.
, w - частота коливання осцилятора. При взаємодії фононів закон збереження імпульсу не виконується: імпульс взаємодіючих фононів може передаватися кристалічній решітці. Уведення фононів є зручним методом опису взаємодії акустичних коливань у кристалах. .
.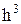 , тому число станів dГ в об'ємі dФ буде дорівнювати
, тому число станів dГ в об'ємі dФ буде дорівнювати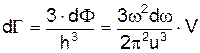 . (3)
. (3)
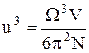
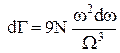 (4)
(4) на частоті w обчислюється так як і у випадку фотонів (формула Планка)
на частоті w обчислюється так як і у випадку фотонів (формула Планка)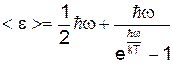 . (5)
. (5)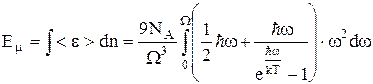
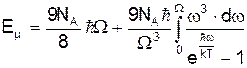 , (6)
, (6) .
.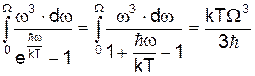 .
. (7)
(7)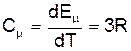 .
.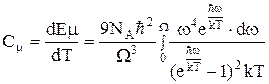 . (8)
. (8) . (9)
. (9)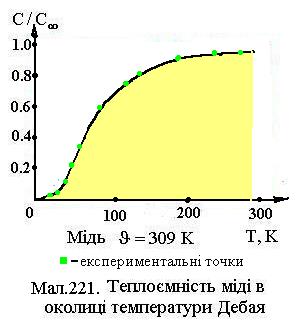
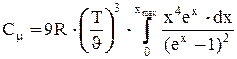 . (10)
. (10)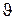 носить назву характеристичної температури Дебаяі визначає граничну температуру кристала, нижче якої теплоємність потрібно визначати на основі квантування акустичного поля. У випадку низьких температур, коли
носить назву характеристичної температури Дебаяі визначає граничну температуру кристала, нижче якої теплоємність потрібно визначати на основі квантування акустичного поля. У випадку низьких температур, коли 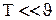 верхня границя інтеграла в (10)
верхня границя інтеграла в (10) 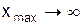 , а сам інтеграл буде деяким числом. При цьому теплоємність буде пропорційна Т3, що відповідає даним експерименту (див.Мал.221). Досліди показують, що одержана залежність теплоємності від температури добре виконується для багатьох хімічно простих речовин, а саме співвідношення відоме, як закон Дебая.
, а сам інтеграл буде деяким числом. При цьому теплоємність буде пропорційна Т3, що відповідає даним експерименту (див.Мал.221). Досліди показують, що одержана залежність теплоємності від температури добре виконується для багатьох хімічно простих речовин, а саме співвідношення відоме, як закон Дебая.
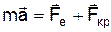 , (1)
, (1)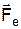 - сила створена зовнішнім електричним, а
- сила створена зовнішнім електричним, а  - кристалічним полями. Але для цього потрібно описати у явному вигляді
- кристалічним полями. Але для цього потрібно описати у явному вигляді 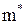 . В основі методу лежить корпускулярно-хвильовий дуалізм електрона: псі-функція електрона у кристалі являє собою хвильовий пакет з несучою частотою
. В основі методу лежить корпускулярно-хвильовий дуалізм електрона: псі-функція електрона у кристалі являє собою хвильовий пакет з несучою частотою 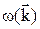 , яка є функцією хвильового вектора
, яка є функцією хвильового вектора  . У такому випадку покладаємо, що швидкість електрона V співпадає із груповою швидкістю Vгр хвильового пакета
. У такому випадку покладаємо, що швидкість електрона V співпадає із груповою швидкістю Vгр хвильового пакета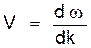 (2)
(2)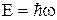 наступним чином
наступним чином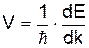 . (3)
. (3)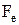 електрон придбаває імпульс
електрон придбаває імпульс  , який зв’язаний з нею другим законом Ньютона
, який зв’язаний з нею другим законом Ньютона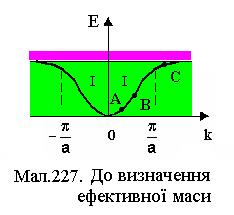
 . ( 4)
. ( 4)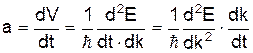 . (5)
. (5)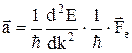 . (6)
. (6)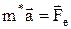 ,
,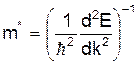 (7)
(7) , у просторі періодичного потенціального поля кристала. У такому випадку властивості криcталічного поля закладаються у залежність енергії Е від хвильового вектора
, у просторі періодичного потенціального поля кристала. У такому випадку властивості криcталічного поля закладаються у залежність енергії Е від хвильового вектора 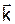 . Ця залежність визначається розв'язком відповідного рівняння Шредінгера. Підсумовуючи розглянуте, можна стверджувати, що метод ефективної маси дає можливість розглянути рух електрона у кристалічному полі під дією зовнішнього електричного поля, як рух вільного електрона, згідно рівняння (6).
. Ця залежність визначається розв'язком відповідного рівняння Шредінгера. Підсумовуючи розглянуте, можна стверджувати, що метод ефективної маси дає можливість розглянути рух електрона у кристалічному полі під дією зовнішнього електричного поля, як рух вільного електрона, згідно рівняння (6).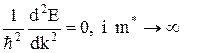
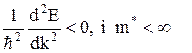
 , (8)
, (8) та співпадає з дослідними даними, на відміну від класичної теорії, де
та співпадає з дослідними даними, на відміну від класичної теорії, де 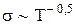 .
.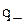 та потенціалом
та потенціалом 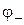 (див. Мал.235). Одночасно на поверхні кристала індукується некомпенсований додатній заряд та потенціал іонів кристалічної решітки тої ж величини, що й в електронної хмарки
(див. Мал.235). Одночасно на поверхні кристала індукується некомпенсований додатній заряд та потенціал іонів кристалічної решітки тої ж величини, що й в електронної хмарки 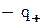 ,
,  . Таким чином над поверхнею кристала створюється подвійний потенціальний бар’єр. Для того щоб електрон вийшов за поверхню кристала, необхідно виконати роботу проти кулонівських сил тяжіння F+, яка викликана поверхневим зарядом q+ та сили відштовхування
. Таким чином над поверхнею кристала створюється подвійний потенціальний бар’єр. Для того щоб електрон вийшов за поверхню кристала, необхідно виконати роботу проти кулонівських сил тяжіння F+, яка викликана поверхневим зарядом q+ та сили відштовхування 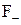 , яка створюється зарядом електронної хмарки
, яка створюється зарядом електронної хмарки  . Ця робота дорівнює
. Ця робота дорівнює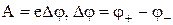 ,
,
 2. Різниця потенціалів між точками поблизу поверхонь кінців ланцюга, створеного з¢єднанням різнорідних провідників, що мають однакову температуру, не залежить від хімічного складу проміжних провідників і дорівнює зовнішній контактній різниці потенціалів, що виникає при безпосередньому з’єднанні крайніх провідників.
2. Різниця потенціалів між точками поблизу поверхонь кінців ланцюга, створеного з¢єднанням різнорідних провідників, що мають однакову температуру, не залежить від хімічного складу проміжних провідників і дорівнює зовнішній контактній різниці потенціалів, що виникає при безпосередньому з’єднанні крайніх провідників.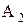 у метал із більшою роботою виходу
у метал із більшою роботою виходу 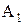 (глибшою потенціальною ямою). При цьому метал з
(глибшою потенціальною ямою). При цьому метал з 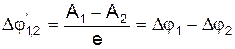 . (1)
. (1)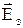 .
. електрони з другого металу дифундують у перший. Цей процес продовжується до вирівнювання концентрацій електронів на границі контакту в обох металах. Розрахунки внутрішньої контактної різниці потенціалів за класичною теорією можна провести у такий спосіб.
електрони з другого металу дифундують у перший. Цей процес продовжується до вирівнювання концентрацій електронів на границі контакту в обох металах. Розрахунки внутрішньої контактної різниці потенціалів за класичною теорією можна провести у такий спосіб.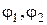 . З класичної точки зору концентрацію електронів у потенціальному електричному полі з відповідним потенціалом при поверхні розділу двох металів за Больцманом можна записати у виді
. З класичної точки зору концентрацію електронів у потенціальному електричному полі з відповідним потенціалом при поверхні розділу двох металів за Больцманом можна записати у виді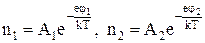 , (2)
, (2) деякі сталі, Т – температура на границі. З (2) можна одержати вирази для потенціалів
деякі сталі, Т – температура на границі. З (2) можна одержати вирази для потенціалів . (3)
. (3) . (4)
. (4) має величину
має величину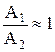 ,
,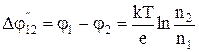 . (5)
. (5) .
.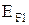 та
та 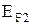 в провідниках. У провідникові, що заряджається позитивно, рівень Фермі знижується, а у метала, що заряджається негативно - підвищується. Процес продовжується до вирівняння рівнів Фермі. Таке явище виникає у зв’язку зі зміною концентрацій електронів, від значення яких залежить величина енергії Фермі. Розглянутий процес спричиняє виникнення внутрішньої різниці потенціалів
в провідниках. У провідникові, що заряджається позитивно, рівень Фермі знижується, а у метала, що заряджається негативно - підвищується. Процес продовжується до вирівняння рівнів Фермі. Таке явище виникає у зв’язку зі зміною концентрацій електронів, від значення яких залежить величина енергії Фермі. Розглянутий процес спричиняє виникнення внутрішньої різниці потенціалів . (3)
. (3)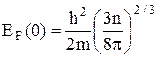 ,
,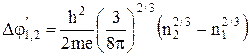 .
. 0 К енергія Фермі має вид
0 К енергія Фермі має вид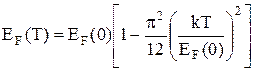 .
.
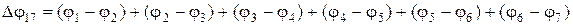
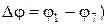 , що й пояснює другий закон Вольта.
, що й пояснює другий закон Вольта.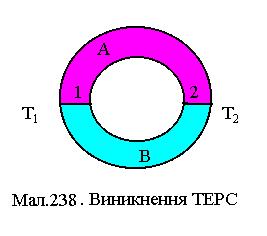 Таким чином створюється стороннє силове поле не електричного походження, яке направлене назустріч градієнту температури, тобто від гарячого до холодного контакту. Такого ж роду процеси відбуваються у замкненому колі з n- та р-напівпровідників. У першому випадку напруженість силового поля направлена, як і у випадку металів, по градієнту поля, а в другому випадку - у протилежному напрямку.
Таким чином створюється стороннє силове поле не електричного походження, яке направлене назустріч градієнту температури, тобто від гарячого до холодного контакту. Такого ж роду процеси відбуваються у замкненому колі з n- та р-напівпровідників. У першому випадку напруженість силового поля направлена, як і у випадку металів, по градієнту поля, а в другому випадку - у протилежному напрямку.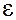 у замкненому колі визначається різницями потенціалів на контактах 1 та 2
у замкненому колі визначається різницями потенціалів на контактах 1 та 2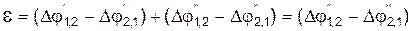
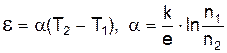 .
.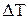 . Однак із більшенням
. Однак із більшенням 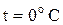 , то при температурі другого спаю при
, то при температурі другого спаю при 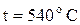 , ТЕРС становиться рівною 0. При температурі меншій
, ТЕРС становиться рівною 0. При температурі меншій 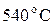 полярність має один знак, а при більшій – інший.
полярність має один знак, а при більшій – інший.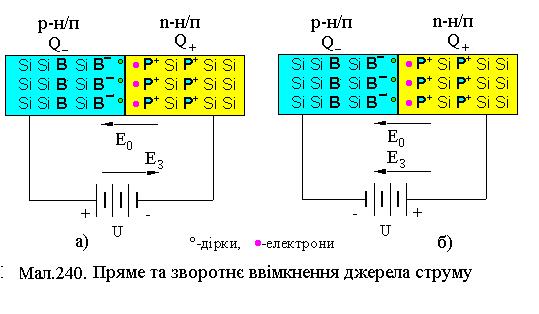
 , направленою від n- до р-області. Це поле протидіє дифузії носіїв струму через контакт. У якийсь час
, направленою від n- до р-області. Це поле протидіє дифузії носіїв струму через контакт. У якийсь час 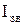 майже відсутній аж до зовнішньої напруги, при якій напівпровідник пробивається - атоми іонізуються. Таке включення напруги (‘+’ на n-область і ‘-’ на р-область) називається зворотнім (див. Мал.240 б)). При накладанні зовнішнього поля з напруженістю
майже відсутній аж до зовнішньої напруги, при якій напівпровідник пробивається - атоми іонізуються. Таке включення напруги (‘+’ на n-область і ‘-’ на р-область) називається зворотнім (див. Мал.240 б)). При накладанні зовнішнього поля з напруженістю 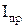 >>
>>  при однаковій величині напруги, що створює ці струми, називається коефіцієнтом випрямлення. Ця величина змінюється при зміні величини напруги. Таким чином, контакт р-n напівпровідників має односторонню провідність електричного струму. Ця властивість зникає коли температура діода підвищується до такої, що власна провідність стає більшою ніж домішкова.
при однаковій величині напруги, що створює ці струми, називається коефіцієнтом випрямлення. Ця величина змінюється при зміні величини напруги. Таким чином, контакт р-n напівпровідників має односторонню провідність електричного струму. Ця властивість зникає коли температура діода підвищується до такої, що власна провідність стає більшою ніж домішкова.


