
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні поняття зонної теоріїСодержание книги Поиск на нашем сайте
Поряд із дозволеною та забороненою енергетичними зонами введемо поняття валентної зони та зони провідності (вільної зони). Перша утворюється з енергетичних рівнів електронів заповнених зовнішніх оболонок атомів, а друга - або частково заповнена валентними електронами, або вільна й утворюється енергетичними рівнями вільних, відірвавшихся від атомів електронів. В залежності від співвідношення між ширинами заборонених зон та наявністю зон провідності кристалічні тіла поділяються на три групи: метали, діелектрики та напівпровідники. Метали. Кристали металу мають частково заповнену зону провідності. Наприклад, розглянемо кристал натрію. Цей атом має 11 електронів у таких станах Діелектрикиабо ізолятори. У випадку, коли валентна зона заповнена повністю при T Напівпровідники(н/п). До класу н/п відносять кристали з вільною зоною провідності і повністю заповненою валентною зоною при T Під дією зовнішнього електричного поля на напівпровідник, в ньому поряд із направленим рухом вільних електронів у зоні виникає направлений рух валентних електронів по вакансіям у валентній зоні (якщо вони є), тобто без відриву від атомів. Цікавим є утворення зон у кристалах елементів четвертої групи, наприклад, кремнію. Ці елементи мають 4 валентних електронів і їх кристали мали б бути металами, так як валентна р-зона містить два електрони на атом і заповнена лише на 1/3. Але експеримент показує, що 3р-зона розчіплюється на дві зони, одна з яких об’єднується з 3s-зоною, а друга виступає як валентна і повністю заповнена при температурі T
Таблиця 1. Характеристики діелектриків та напівпровідників.
Електропровідність металів а). Рівняння динаміки руху електронів. Метод ефективної маси Для дослідження руху електронів у періодичному полі кристала достатньо записати та розв'язати рівняння другого закону Ньютона
де m-класична маса електрона,
і може бути визначена через його енергію
Під дією зовнішньої сили
Величину прискорення електрона можна визначити з (3) таким чином
Враховуючи (4), маємо
Вираз (6) можна представити у вигляді рівняння другого закону Ньютона для електрона
де
так звана ефективна маса електрона. Цю масу можна тлумачити як міру інертності електрона до дії зовнішньої сили Знаючи залежність Е від k, можна визначити
У точках перегину кривої (точка В) друга похідна від Е(k)
Це означає, що електрони, які знаходяться посередині енергетичної зони, беруть обмежену участь в електропровідності. На верхніх енергетичних рівнях, під стелею першої зони Брилюєна (точка С), Е має максимум:
Це означає, що під дією сили б). Квантова теорія електропровідності металів
Як показують квантово-механічні розрахунки величина провідності s металів з уведенням ефективної маси
де n- концентрація вільних електронів із зарядом e, t - час релаксації (фактично час вільного пробігу). Щодо температурної залежності s, то до Т=50 К вона Зазначимо, що опір направленому рухові електронів під дією зовнішнього електричного поля пов'язаний з розсіюванням їх на тепловому коливальному русі вузлів кристалічної решітки (фононах) та її дефектах, домішках, вакансіях і механічних неоднорідностях.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 314; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.51.72 (0.006 с.) |

 . Усі оболонки, крім 3s, заповнені, а в останній знаходиться один електрон. При утворенні кристала з відповідних оболонок утворюються енергетичні зони. З них - зона, що відповідає валентній оболонці, заповнена наполовину, і є зоною провідності. На відміну від Na, в атомі магнію Mg, який має 12 електронів, оболонка 3s заповнена, але кристал є хорошим провідником. Це пов'язано з тим, що при утворенні кристала магнію, його кристалічне поле деформує зони так, що в результаті існує перекриття сусідніх 3s та 3p зон. У зв'язку з цим у Mg 3p зона є зоною провідності.
. Усі оболонки, крім 3s, заповнені, а в останній знаходиться один електрон. При утворенні кристала з відповідних оболонок утворюються енергетичні зони. З них - зона, що відповідає валентній оболонці, заповнена наполовину, і є зоною провідності. На відміну від Na, в атомі магнію Mg, який має 12 електронів, оболонка 3s заповнена, але кристал є хорошим провідником. Це пов'язано з тим, що при утворенні кристала магнію, його кристалічне поле деформує зони так, що в результаті існує перекриття сусідніх 3s та 3p зон. У зв'язку з цим у Mg 3p зона є зоною провідності. K, а зона провідності не має електронів і відстань DЕ між цими зонами (ширина забороненої зони) становить декілька еВ (> 5 еВ), то кристал відноситься до діелектриків. Під дією електричного або теплового поля електрони з валентної зони не можуть перейти у зону провідності. Виключення становить електричний пробій діелектрика - електрична іонізація атомів криcтала. До таких кристалів відносяться, наприклад, NaCl із DЕ= 6 еВ, вуглець С із DЕ= 5,2 еВ та інші.
K, а зона провідності не має електронів і відстань DЕ між цими зонами (ширина забороненої зони) становить декілька еВ (> 5 еВ), то кристал відноситься до діелектриків. Під дією електричного або теплового поля електрони з валентної зони не можуть перейти у зону провідності. Виключення становить електричний пробій діелектрика - електрична іонізація атомів криcтала. До таких кристалів відносяться, наприклад, NaCl із DЕ= 6 еВ, вуглець С із DЕ= 5,2 еВ та інші.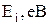
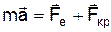 , (1)
, (1)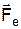 - сила створена зовнішнім електричним, а
- сила створена зовнішнім електричним, а  - кристалічним полями. Але для цього потрібно описати у явному вигляді
- кристалічним полями. Але для цього потрібно описати у явному вигляді 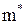 . В основі методу лежить корпускулярно-хвильовий дуалізм електрона: псі-функція електрона у кристалі являє собою хвильовий пакет з несучою частотою
. В основі методу лежить корпускулярно-хвильовий дуалізм електрона: псі-функція електрона у кристалі являє собою хвильовий пакет з несучою частотою 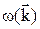 , яка є функцією хвильового вектора
, яка є функцією хвильового вектора  . У такому випадку покладаємо, що швидкість електрона V співпадає із груповою швидкістю Vгр хвильового пакета
. У такому випадку покладаємо, що швидкість електрона V співпадає із груповою швидкістю Vгр хвильового пакета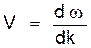 (2)
(2)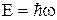 наступним чином
наступним чином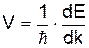 . (3)
. (3)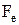 електрон придбаває імпульс
електрон придбаває імпульс  , який зв’язаний з нею другим законом Ньютона
, який зв’язаний з нею другим законом Ньютона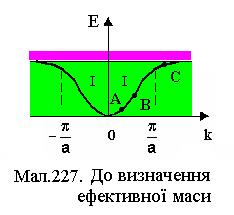
 . ( 4)
. ( 4)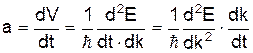 . (5)
. (5)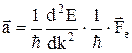 . (6)
. (6)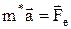 ,
,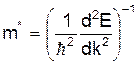 (7)
(7) , у просторі періодичного потенціального поля кристала. У такому випадку властивості криcталічного поля закладаються у залежність енергії Е від хвильового вектора
, у просторі періодичного потенціального поля кристала. У такому випадку властивості криcталічного поля закладаються у залежність енергії Е від хвильового вектора 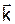 . Ця залежність визначається розв'язком відповідного рівняння Шредінгера. Підсумовуючи розглянуте, можна стверджувати, що метод ефективної маси дає можливість розглянути рух електрона у кристалічному полі під дією зовнішнього електричного поля, як рух вільного електрона, згідно рівняння (6).
. Ця залежність визначається розв'язком відповідного рівняння Шредінгера. Підсумовуючи розглянуте, можна стверджувати, що метод ефективної маси дає можливість розглянути рух електрона у кристалічному полі під дією зовнішнього електричного поля, як рух вільного електрона, згідно рівняння (6).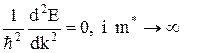
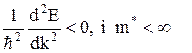
 , (8)
, (8)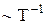 та співпадає з дослідними даними, на відміну від класичної теорії, де
та співпадає з дослідними даними, на відміну від класичної теорії, де 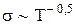 .
.


