
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: розв’язання задач на основні закони розподілу неперервних випадкових величин.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Приклад 1. Випадкова величина рівномірно розподілена на проміжку [4; 16]. Знайти Розв’язання. Згідно з формулами:
Числові характеристики НВВ Х, що рівномірно розподілена: Ймовірність того, що рівномірно розподілена ВВХ потрапить в проміжок
Приклад 2. Задано Визначити Розв’язання. Так задана випадкова величина, розподілена за показниковим розподілом з параметром
Приклад 3. Відомо, що випадкова величина Х має закон розподілу Записати вирази для Розв’язання.
  Графіки Графіки  наведені на рис. 1 і 2. наведені на рис. 1 і 2.
Рис.1. Рис. 2. Використовуючи формули
1)
2)
Індивідуальні завдання 9 1. Випадкова величина
2. Випадкова величина має показниковий розподіл з параметром
3. Випадкова величина має нормальний розподіл з параметрами
Практичне заняття № 10 Тема: Використання граничних теорем та законів великих чисел для оцінки ймовірностей у випадку великої кількості випробувань. Приклад 1. Відомо, що Розв’язання.
Використаємо нерівність Чебишева:
Приклад 2. Визначити необхідне число дослідів, які необхідно провести, щоб з ймовірністю 0,96 відхилення частоти появи події А від ймовірності її появи в окремому досліді, що дорівнює 0,75, не перевищувало за абсолютною величиною 0,05. Розв’язання. Введемо позначення
а) нерівність Чебишева:
б) інтегральну теорему Муавра-Лапласа про ймовірність відхилення частоти події від її імовірності в кожному випробуванні не більше, ніж на
Як видно з розрахунків, нерівність Чебишева дає значення n значно вище. Індивідуальні завдання 10 Завдання 1. Кількість повідомлень, що надходять на телефонний номерза добу є випадковою величиною, математичне сподівання якої дорівнює Завдання 2. Аналіз торгівельної діяльності певного магазину показує, що середньомісячний товарообіг складає Завдання 3. Ймовірність спотворення цифрового сигналу під час його передачі дорівнює 0,05. Скільки необхідно надіслати сигналів, щоб з ймовірністю не менше Практичне заняття № 11 Тема: Статистичний розподіл вибірки. Графічне зображення вибірки. Обчислення числових характеристик вибірки. Приклад 1. Задана вибірка із 50 елементів:
Виконати наступні завдання: 1) побудувати статистичний розподіл вибірки, емпіричну функцію розподілу, та її графік; 2) побудувати полігон та гістограму частот та відносних частот; 3) обчислити числові характеристики вибірки: середнє, дисперсію і середнє квадратичне відхилення; 4) знайти моду, медіану, розмах і коефіцієнт варіації; 5) знайти асиметрію і ексцес вибірки. (N – номер варіанта). Практичне заняття № 12 Тема: Статистичні оцінки. Приклад 1. Автотранспортна компанія має на меті оцінити середній час транспортування овочів та фруктів з півдня країни до столиці. Випадкова вибірка Розв’язання. Довірчий інтервал для середнього
З таблиці функції Лапласа Відповідь: Приклад 2. Проводиться аналіз розмірів основних фондів 15 промислових підприємств регіону. В результаті виявлено, що середнє відхилення складає 0,2 млн.грн. Припускаючі, що розмір основних фондів має нормальний розподіл, знайти межі в яких з надійністю Розв’язання. Межі інтервалу для генерального середнього квадратичного відхилення: Значення З додатку 6 Довірчі інтервали Остаточно Довірчий інтервал для генерального середнього квадратичного відхилення З надійністю 0,9 дисперсія розмірів основних фондів знаходиться в межах 0,0253 – 0,0913, а середнє квадратичне відхилення від 0,1591 млн.грн. до 0,5022 млн.грн. Приклад 3. Визначити обсяг вибірки Розв’язання. Використовуємо формулу: Величину Маємо Індивідуальна робота 12 1. Досліджується вартість доби відпочинку на зимовому курорті. Вибірка об’єму 2. Визначити обсяг вибірки
Практичне заняття № 13
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1072; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.113 (0.009 с.) |

 , побудувати графіки функцій
, побудувати графіки функцій  та
та 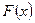 , обчислити ймовірності подій
, обчислити ймовірності подій  та
та  .
.
 .
. за умови
за умови  вираховується за формулою
вираховується за формулою  , враховуючи, що
, враховуючи, що  та
та  маємо
маємо


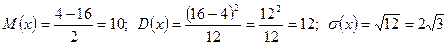 .
.

 .
. . Використовуючи формули
. Використовуючи формули  ;
;  одержимо:
одержимо: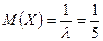 , оскільки
, оскільки 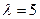 ;
;  ;
;  ;
; ;
;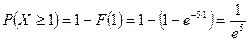 .
. .
.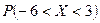 ,
, 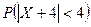 . Чому дорівнюють
. Чому дорівнюють  ?
?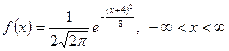 ;
; .
.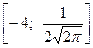

 ;
; , обчислюємо ймовірності:
, обчислюємо ймовірності:
 ;
;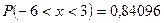 .
.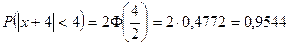 .
. .
. .
.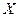 рівномірно розподілена на проміжку
рівномірно розподілена на проміжку  . Знайти
. Знайти  , побудувати графіки функцій
, побудувати графіки функцій  та
та 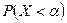


 та
та  .
. та
та  . Записати вирази для
. Записати вирази для  , схематично побудувати їх графіки. Знайти ймовірності
, схематично побудувати їх графіки. Знайти ймовірності  .
.

 всієї продукції, що виробляється заводом – першого сорту. Оцінити ймовірність того, що число виробів першого сорту серед 200 000 виробів виготовлених буде відрізнятися від математичного сподівання цього числа не більше, ніж на 2000 шт.
всієї продукції, що виробляється заводом – першого сорту. Оцінити ймовірність того, що число виробів першого сорту серед 200 000 виробів виготовлених буде відрізнятися від математичного сподівання цього числа не більше, ніж на 2000 шт. – ймовірність того, що виріб І сорту,
– ймовірність того, що виріб І сорту,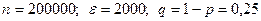
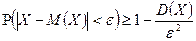 , тут
, тут  ;
;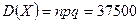 , отже,
, отже, 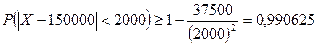 .
. ;
; . Для обчислення кількості дослідів n можна використати дві формули:
. Для обчислення кількості дослідів n можна використати дві формули: , звідки
, звідки  підставивши у формулу, маємо:
підставивши у формулу, маємо:  отже
отже  ;
; :
: знайдемо
знайдемо 
 тобто
тобто  за таблицями інтегральної функції
за таблицями інтегральної функції  отже
отже  ,
,  .
. Оцінити ймовірність того, що в найближчу добу кількість повідомлень: а) перевищить число
Оцінити ймовірність того, що в найближчу добу кількість повідомлень: а) перевищить число  б) на перевищить
б) на перевищить 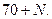
 у.г.о. Оцінити ймовірність того, що в наступному місяці товарообіг буде в межах
у.г.о. Оцінити ймовірність того, що в наступному місяці товарообіг буде в межах  у.г.о., якщо відомо, що дисперсія досліджуваної величини
у.г.о., якщо відомо, що дисперсія досліджуваної величини 
 очікувати, що число спотворених сигналів буде відхилятися від математичного сподівання на величину, що по модулю не перевищує
очікувати, що число спотворених сигналів буде відхилятися від математичного сподівання на величину, що по модулю не перевищує  Розв’язати задачу а) за нерівністю Чебишова; б) за інтегральною теоремою Муавра-Лапласа.
Розв’язати задачу а) за нерівністю Чебишова; б) за інтегральною теоремою Муавра-Лапласа.
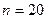 партій товарів показала
партій товарів показала  годин;
годин;  год. Побудувати довірчий інтервал з
год. Побудувати довірчий інтервал з 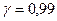 для середнього часу транзиту.
для середнього часу транзиту. Тут
Тут 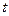 обчислюється з рівності
обчислюється з рівності  за таблицею функції Лапласа.
за таблицею функції Лапласа.
 Межі інтервалу:
Межі інтервалу: 

 знаходяться генеральна дисперсія та середнє квадратичне відхилення розмірів основних фондів.
знаходяться генеральна дисперсія та середнє квадратичне відхилення розмірів основних фондів.
 та
та 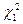 знаходимо у додатку 6 (критичні точки розподілу
знаходимо у додатку 6 (критичні точки розподілу  ) з рівностей
) з рівностей 
 Маємо при
Маємо при  Кількість ступенів свободи
Кількість ступенів свободи 







 за якого похибка
за якого похибка 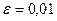 гарантується з ймовірністю 0,97, якщо
гарантується з ймовірністю 0,97, якщо 
 Величина відхилення
Величина відхилення 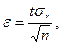 звідси
звідси 

 З таблиці
З таблиці 
 Об’єм вибірки має складати
Об’єм вибірки має складати 
 , та виправлену дисперсію
, та виправлену дисперсію  Побудувати довірчий інтервал з рівнем довіри
Побудувати довірчий інтервал з рівнем довіри  для генеральної середньої
для генеральної середньої  генеральної дисперсії
генеральної дисперсії  та генерального середнього квадратичного відхилення
та генерального середнього квадратичного відхилення  випадкової величини х – вартості доби відпочинку на зимовому курорті.
випадкової величини х – вартості доби відпочинку на зимовому курорті. , якщо
, якщо 



