

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Тема: перевірка гіпотез про розподіл генеральної сукупності за критеріями пірсона та колмогорова
Похожие статьи вашей тематики
Приклад. За спостереженнями, наведеними в таблиці, за допомогою критерію Пірсона перевірити гіпотезу про те, що випадкова величина має нормальний розподіл ( =0,05, n=500). =0,05, n=500).
| Інтервал
| [-4,3)
| [-3,-2)
| [-2,-1)
| [-1,0)
| [0,1)
| [1,2)
| [2,3)
| [3,4)
| | ni
|
|
|
|
|
|
|
|
|
Розв’язання. Обчислимо за вибіркою оцінки параметрів нормального розподілу, використовуючи метод умовних варіант: 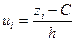 , тут С = – 0,5; h =1. , тут С = – 0,5; h =1.
| №
| Середина інтервалу yі
| Частота
ni
| ui
| ni ui
| ni ui2
| |
| -3,5
-2,5
-1,5
-0,5
0,5
1,5
2,5
3,5
|
| -3
-2
-1
| -30
-60
-70
|
| | ∑
|
|
|
|
|
| 



Знайдемо  . Для знаходження теоретичних частот складають розрахункову таблицю: . Для знаходження теоретичних частот складають розрахункову таблицю:
| №
| 
| 
| Ф( ) )
| Ф( ) )
| pi= Ф( ) – Ф( ) – Ф( ) )
| npi
| |
| ∞
 2,09
–1,42
–0,74
–0,07
0,61
1,28
1,96 2,09
–1,42
–0,74
–0,07
0,61
1,28
1,96
| –2,09
–1,42
–0,74
–0,07
0,61
1,28
1,96
-∞
| –0,5
–2
–1
| –30
–0,48169
–0,42220
–0,27035
–0,02790
0,22907
0,39973
0,47500
| 0,01831
0,05949
0,15185
0,24245
0,25697
0,17066
0,07527
0,025
| 9,155
29,745
75,925
121,225
128,485
85,33
37,635
12,5
| | ∑
|
|
|
|
| 1,000
|
| Порівняємо теоретичні і емпіричні (статистичні) частоти. Для знаходження емпіричного значення  складають розрахункову таблицю: складають розрахункову таблицю:
| №
| ni
| npi
| ni- npi
| (ni - npi)2
| (ni - npi)2/ npi
| |
|
| 9,155
29,745
75,925
121,225
128,485
85,330
37,635
12,5
| 0,845
0,255
–5,925
8,775
–8,485
4,670
2,365
–2,5
| 0,7140
0,0650
35,1056
77,0006
71,9952
21,8089
5,5932
6,25
| 0,07799
0,03663
0,46237
0,63519
0,00778
0,25558
0,14862
0,5
| | ∑
|
|
|
|
| 2,12416
| Отже,  =2,12416. Кількість інтервалів r=8, а кількість невідомих параметрів l =2. Тоді, число степенів свободи k = r – l – 1 = 5. За таблицею розподілу =2,12416. Кількість інтервалів r=8, а кількість невідомих параметрів l =2. Тоді, число степенів свободи k = r – l – 1 = 5. За таблицею розподілу  2 знаходимо критичну точку 2 знаходимо критичну точку 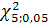 =11,07. Отже, оскільки =11,07. Отже, оскільки  , гіпотеза про нормальний розподіл досліджуваної величини приймається. Рівень достовірності проведеного тесту , гіпотеза про нормальний розподіл досліджуваної величини приймається. Рівень достовірності проведеного тесту  . .
Індивідуальні завдання 13
Розподіл трьохсот приватних фірм за рівнем прибутку (тис.грн за певний часовий проміжок) відображено в наступній таблиці. За допомогою  критерію при рівні значущості критерію при рівні значущості  перевірити гіпотезу про те, що рівень прибутку приватних фірм є нормально розподіленою випадковою величиною. перевірити гіпотезу про те, що рівень прибутку приватних фірм є нормально розподіленою випадковою величиною.
| Рівень прибутку (тис.грн.)
| Кількість фірм
| Рівень прибутку (тис.грн.)
| Кількість фірм
| | [ –K; 0)
(фірма збиткова)
|
| [ 4K; 5K)
| 200-2N
| | [ 0; K)
|
| [ 5K; 6K)
| N+25
| | [ K; 2K)
|
| [ 6K; 7K)
|
| | [ 2K; 3K)
|
| [ 8K; 9K)
|
| | [ 3K; 4K)
| N+20
| [ 9K; 10K)
|
|
Числові значення параметрів:
N – номер варіанту; K – кількість літер у прізвищі.
Практичне заняття № 14
Тема. Використання критерію Фішера-Снедекора.
Приклад 1. Рівень впливу фактора F на ознаку Х наведено у таблиці
| Рівень фактора F
(групи)
| Спостережувані значення
ознаки Х
|  1 1
 2 2
| 51, 52, 56, 57
52, 54, 56, 58
42, 44, 50, 52
|
Дослідити, чи істотно впливає фактор F на ознаку Х при рівні значущості  . .
Розв’язування. На ознаку Х діє фактор F, який має три рівня ( ). Число спостережень на кожному рівні однакове і дорівнює чотирьом ( ). Число спостережень на кожному рівні однакове і дорівнює чотирьом ( ). ).
Обчислимо групові середні  та загальну середню та загальну середню  : :
 , ,  , ,
 , , 
Знаходимо факторну  і залишкову і залишкову  суми квадратів відхилень: суми квадратів відхилень:

Поділивши одержані суми квадратів відхилень на відповідні числа ступенів свободи, одержимо факторну і залишкову дисперсії
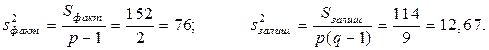
Порівняємо факторну і залишкову дисперсії за критерієм Фішера–Снедекора, обчисливши спостережуване значення критерію

Число ступенів свободи чисельника  а знаменника а знаменника 
За значеннями  , ,   по таблиці критичних точок розподілу Фішера–Снедекора знаходимо критичну точку по таблиці критичних точок розподілу Фішера–Снедекора знаходимо критичну точку

Висновок: Оскільки  , то вплив фактора F на ознаку Х є суттєвим. , то вплив фактора F на ознаку Х є суттєвим.
Індивідуальні завдання 14
З’ясувати, чи істотно впливає фактор F на ознаку Х при заданих рівнях значущості 
Варіант,

| Рівень
фактора
| Спостережувані
значення Х
| Варіант,

| Рівень
фактора
| Спостережувані
значення Х
|

|
| 3,4; 4,2; 5,1; 4,3; 4,6
3,8; 3,6; 4,5; 5,2; 5,1
4,3; 5,6; 5,2; 4,9; 4,7
3,6; 3,9; 4,3; 5,4; 5,0
|

|
| 9,4; 8,2; 7,1; 8,3; 7,6
8,8; 9,6; 7,5; 8,2; 9,1
8,3; 9,6; 8,2; 7,9; 8,7
7,6; 8,9; 9,3; 7,4; 9,0
|

|
| 18; 24; 21; 25
23; 25; 21; 20
19; 17; 22; 21
18; 22; 24; 23
23; 21; 24; 26
|

|
| 234; 321; 269; 308
338; 353; 289; 331
278; 312; 329; 358
332; 371; 369; 328
264; 338; 289; 352
|

|
| 126; 143; 132; 152
135; 148; 145; 153
129; 134; 136; 143
132; 143; 152; 147
|

|
| 7,24; 6,32; 7,36; 6,31
6,41; 5,35; 5,43; 6,29
7,35; 6,38; 7,32; 6,41
6,38; 5,35; 6,33; 5,43
|

|
| 1,24; 1,32; 1,36; 1,31
1,41; 1,35; 1,43; 1,29
1,35; 1,38; 1,32; 1,40
1,38; 1,35; 1,33; 1,42
|

|
| 4,24; 5,32; 5,36; 5,31
4,41; 4,35; 4,43; 5,29
5,35; 5,38; 5,32; 5,40
4,38; 5,35; 5,33; 4,42
|

|
| 0,23; 0, 24; 0,21; 0,25
0,23; 0,25; 0,21; 0,20
0,19; 0,17; 0,22; 0,21
0,18; 0,22; 0,24; 0,23
|

|
| 0,73; 0, 84; 0,71; 0,65
0,63; 0,85; 0,71; 0,69
0,79; 0,67; 0,72; 0,81
0,78; 0,82; 0,64; 0,73
|

|
| 13; 15; 17; 11; 14; 12
10; 13; 14; 16; 18; 12
15; 17; 14; 18; 21; 20
|

|
| 51; 65; 57; 71; 64; 72
70; 63; 54; 66; 68; 71
65; 57; 74; 68; 71; 70
|

|
| 1,4; 1,5; 1,7; 1,1; 1,2
1,1; 1,5; 1,8; 1,6; 1,9
1,6; 1,9; 1,7; 1,8; 2,1
|

|
| 7,46; 7,52; 7,70; 7,82
7,86; 8,52; 8,73; 7,64
7,35; 8,02; 8,15; 7,26
|

|
| 64; 69; 74; 58; 71
53; 67; 59; 68; 58
56; 70; 65; 72; 63
63; 64; 54; 71; 57
|

|
| 4,4; 5,9; 5,4; 5,8; 5,1
5,3; 5.7; 4,9; 4,8; 4,6
5,6; 4,7; 5,5; 5,2; 4,3
5,3; 5,4; 4,8; 4,7; 4,9
|

|
| 10,3; 13,2; 15,3; 12,6
14,4; 15,4; 13,6; 12,8
12,1; 15,9; 15,3; 13,5
15,1; 13,9; 14,3; 13,8
|

|
| 80,7; 83,2; 85,3; 82,6
84,4; 85,4; 83,6; 82,8
82,1; 85,9; 85,3; 83,5
85,9; 83,9; 84,7; 88,5
|

|
| 426; 443; 432; 452
435; 448; 465; 453
429; 434; 456; 443
432; 463; 452; 447
|

|
| 2,6; 3,1; 3,4; 2,8; 3,3
2,9; 3,6; 3,2; 2,8; 3,7
3,6; 3,7; 3,0; 3,8; 3,1
2,5; 2,3; 3,2; 2,8; 3,6
|

|
| 36; 45; 49; 32
56; 55; 48; 52
46; 45; 54; 53
46; 60; 59; 57
56; 58; 47; 62
|

|
| 76; 85; 79; 82
86; 85; 78; 72
76; 75; 84; 73
86; 76; 79; 77
86;88; 87; 92
|

|
| 6; 5; 9; 7; 8;10
5;9; 8; 6; 7; 6
8; 5; 8; 5; 9; 7
6; 10; 9; 7; 8; 7
5; 9; 7; 6; 7; 8
|

|
| 3,3; 4,7; 4,8; 3,2
5,8; 5,7; 4,9; 5,2
4,6; 4,5; 5,4; 5,3
4,6; 6,0; 5,9; 5,7
5,6; 5,8; 4,7; 6,2
|

|
| 0,68; 0,61; 0,76; 0,59
0,78; 0,73; 0,71; 0,67
0,60; 0,69; 0,72; 0,56
0,72; 0,66; 0,81; 0,84
|

|
| 0,18; 0,11; 0,16; 0,19
0,18; 0,13; 0,11; 0,17
0,16; 0,19; 0,12; 0,16
0,12; 0,16; 0,11; 0,14
|

|
| 76,4; 82,2; 90,6; 87,5
70,7; 78,2; 80,9; 84,3
86,2; 89,1; 92,6; 88,6
79,2; 85,2; 89,4; 81,5
|

|
| 6,4; 8,2; 9,6; 8,5
7,7; 7,2; 8,9; 8,3
8,2; 8,1; 9,6; 8,6
7,2; 8,2; 8,4; 8,5
|

|
| 578; 654; 679; 523; 749
537; 554; 619; 523; 628
707; 662; 670; 723; 687
768; 762; 696; 729; 674
|

|
| 5,8; 6,5; 6,7; 5,3; 7,4
5,7; 5,5; 6,1; 5,3; 6,2
7,0; 6,6; 6,7; 7,2; 6,8
7,6; 7,2; 6,9; 7,2; 6,7
|

|
| 1,5; 1,8; 2,1; 1,7
1,7; 1,9; 2,0; 2,4
2,1; 1,7; 2,2; 2,6
1,6; 1,9; 1,4; 1,8
1,7; 1,9; 2,0; 2,4
|

|
| 4,5; 4,8; 4,1; 4,7
4,7; 4,9; 5,0; 5,4
4,1; 4,7; 5,2; 4,6
4,6; 4,9; 5,4; 4,8
4,2; 4,9; 5,0; 4,5
|

|
| 30,3; 43,2; 45,3; 32,6
34,4; 45,4; 43,6; 42,8
32,1; 35,9; 35,3; 43,5
35,1; 43,9; 34,3; 43,8
|

|
| 70,3; 73,2; 75,3; 72,6
84,4; 85,4; 73,6; 82,8
72,1; 75,9; 85,3; 83,5
75,1; 83,9; 84,3; 73,8
|
Практичне заняття № 15
|



 =0,05, n=500).
=0,05, n=500).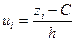 , тут С = – 0,5; h =1.
, тут С = – 0,5; h =1.



 . Для знаходження теоретичних частот складають розрахункову таблицю:
. Для знаходження теоретичних частот складають розрахункову таблицю:

 )
)
 )
)
 2,09
–1,42
–0,74
–0,07
0,61
1,28
1,96
2,09
–1,42
–0,74
–0,07
0,61
1,28
1,96
 складають розрахункову таблицю:
складають розрахункову таблицю: 2 знаходимо критичну точку
2 знаходимо критичну точку 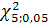 =11,07. Отже, оскільки
=11,07. Отже, оскільки  , гіпотеза про нормальний розподіл досліджуваної величини приймається. Рівень достовірності проведеного тесту
, гіпотеза про нормальний розподіл досліджуваної величини приймається. Рівень достовірності проведеного тесту  .
. критерію при рівні значущості
критерію при рівні значущості  перевірити гіпотезу про те, що рівень прибутку приватних фірм є нормально розподіленою випадковою величиною.
перевірити гіпотезу про те, що рівень прибутку приватних фірм є нормально розподіленою випадковою величиною. 1
1
 2
2
 .
. ). Число спостережень на кожному рівні однакове і дорівнює чотирьом (
). Число спостережень на кожному рівні однакове і дорівнює чотирьом ( ).
). та загальну середню
та загальну середню  :
: ,
,  ,
, ,
, 
 і залишкову
і залишкову  суми квадратів відхилень:
суми квадратів відхилень:
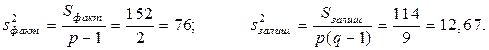

 а знаменника
а знаменника 

 по таблиці критичних точок розподілу Фішера–Снедекора знаходимо критичну точку
по таблиці критичних точок розподілу Фішера–Снедекора знаходимо критичну точку
 , то вплив фактора F на ознаку Х є суттєвим.
, то вплив фактора F на ознаку Х є суттєвим.




