
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: означення ймовірності. Елементи комбінаторики та теорії множин.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Практичне заняття № 1 Тема: Означення ймовірності. Елементи комбінаторики та теорії множин. Приклад 1. З карток з цифрами 1; 2; 3; 4; 5 навмання вибирають три картки, розкладають їх у ряд і фіксують утворене число. Вкажіть загальну кількість елементарних подій даного експерименту і кількість елементарних подій, які сприяють події В =„Утворилося число кратне 3”. Розв’язання. Для вибраних трьох карток важливим є порядок, тому для підрахунку загальної кількості елементарних подій використаємо розміщення Події В сприяє поява числа, сума цифр якого ділиться на три. Серед даних цифр виберемо всі трійки таких, щоб їх сума ділиться на 3: 1, 2, 3 або 1, 3, 5, або 2, 3, 4, або 3, 4, 5. З кожної такої трійки цифр можна утворити Приклад 2. У скарбниці є 200 монет одного номіналу, серед яких 25 монет 1992 року випуску. Яка ймовірність того, що навмання вибрана монета датована 1992 роком? Розв’язання. Експеримент полягає у вийманні зі скарбнички навмання однієї монети і фіксації її року випуску. Враховуючи, що монети одного номіналу, тому мають однакову вагу і величину вважаємо, що жодна монета не має переваги над іншими бути вибраною. Тому наслідки експерименту вважаємо рівноможливими. Цим самим імовірнісну модель побудовано. Подія А – „вийнята монета 1992 року”. Всього наслідків експерименту є 200. Події А сприяють 25 наслідків, тому Приклад 3. Двоє осіб домовились зустрітися в певному місці у проміжку часу від Розв’язання. Простір Представлені умови зобразимо на площині в системі координат
Рис. 1. Скориставшись геометричним означенням ймовірності дістанемо:
Індивідуальні завдання 1 1. У квадрат з вершинами (0;0), (0;1), (1;0), (1;1) навмання кинули точку М. Нехай ( 2. За підсумком року акції (N – номер варіанта; k – кількість букв в повному імені). 3. У ящику знаходяться кульки пронумеровані від 1 до 200. Навмання дістають одну кульку. Яка ймовірність того, що дане число буде кратне числам 1-10 варіант: 11-20 варіант: 21-35 варіант: Практичне заняття № 2 Індивідуальні завдання 2 1. Податкові інспектори здійснюють перевірку діяльності підприємств: перший обслуговує а підприємств, серед яких с % не мають заборгованості, другий - b підприємств, із них d % - без заборгованості. Яка ймовірність того, що: а) навмання обране підприємство не має заборгованості; б) підприємство, що не має заборгованості, перевіряв перший інспектор? 2. У рекламному агентстві працює три групи дизайнерів. Перша обслуговує l фірм, друга – k, третя – m. Протягом одного місяця кошти, витрачені на рекламу дизайнерами першої групи, повертаються до z% фірм, другої – до h%, третьої – до v%. Яка ймовірність того, що: а) навмання вибрана фірма окупила витрачені на рекламу кошти протягом місяця; б) фірма, що окупила протягом місяця витрачені на рекламу кошти, обслуговувалася першою групою дизайнерів? 3. У першій групі 40-N студентів, у другій 18 студентів. В кожній з груп по два студенти, що не підготувалися до семінару. З кожної групи викликають по одному студенту. Яка ймовірність того, що а) обидва студенти підготувалися до семінару; б) один студент підготувався до семінару; в) хоча б один студент підготувався до семінару; г) обидва студенти не підготувалися до семінару. 4. Ймовірність своєчасної сплати податків для першого підприємства дорівнює
Практичне заняття № 3 Індивідуальне завдання 3 1. Робітник обслуговує n верстатів-автоматів. Імовірність того, що протягом години верстат-автомат потребує уваги робітника, є величиною сталою і дорівнює 1) k верстатів; 2) від k 1 до k 2 верстати; 3) неменше ніж m верстатів; 4) не більше ніж m1 верстат; 5) принаймні один верстат. 2. Імовірність того, що студент складе іспит з теорії ймовірностей, є величиною сталою і дорівнює в середньому
Практичне заняття № 4 Індивідуальні завдання 4 1. Знайти імовірність того, що подія А настає рівно m раз у n випробуваннях, якщо імовірність появи події А у кожному випробуванні дорівнює р. 2. Імовірність того, що деталь не пройшла перевірки ВТК, дорівнює р. Знайти імовірність того, що серед n випадково відібраних деталей виявиться неперевіреними від k 1 до k 2 деталей. 3. Імовірність випуску бракованого виробу дорівнює р. Чому дорівнює імовірність того, що у партії із n виробів бракованих буде не більше як m? 4. Ймовірність появи події в схемі незалежних випробувань Бернуллі є сталою в межах схеми і рівною
Практична робота 5
Індивідуальні завдання 5 Завдання 1. Розв’язати задачу, представлену в прикладі 1, покладаючи Завдання 2. Розв’язати задачу, представлену в прикладі 2, покладаючи Завдання 3. Розв’язати задачу, представлену в прикладі 3 при таких значеннях Варіанти 1-10: Варіанти 11-20: Варіанти 21-30: Варіанти 31-35: де К - номер Вашого варіанта. Завдання 4. Випадкова величина Практичне завдання № 6 Тема:Обчислення числових характеристик системи двох дискретних випадкових величин. Приклад 1. Система двох дискретних випадкових величин
1. Знайти невідомий параметр системи 2. Знайти ряди розподілу кожної випадкової величини 3. Обчислити числові характеристики системи 4. Знайти умовний закон розподілу ДВВ 5. Знайти умовний закон розподілу ДВВ 6. Знайти закон розподілу ДВВ 7. Обчислити імовірність події Розв’язання. 1. Умова нормування ряду розподілу системи ДВВ Маємо:
Маємо остаточно закон розподілу
1. Знайдемо ряд розподілу одновимірної ДВВ
Отже, маємо ряд розподілу для ДВВ
Одновимірна функція цього розподілу Знайдемо ряд розподілу для ДВВ
Отже, маємо закон розподілу ДВВ
Одновимірна функція розподілу
2. Обчислимо числові характеристики для системи ДВВ
Обчислимо кореляційний момент
Отже, Оскільки
Оскільки Коефіцієнт кореляції:
Оскільки 3. Знайдемо умовний закон розподілу ДВВ Користаючи формулою умовної імовірності
Отже, маємо умовний закон розподілу ДВВ
Зауваження.Імовірність події 5. Знайдемо умовний закон розподілу ДВВ X при умові
Отже, умовний закон розподілу ДВВ X при умові
Зауваження.Імовірність 6. Знайдемо закон розподілу ДВВ Розмістимо у правих верхніх кутах клітин закону розподілу системи ДВВ
Маємо:
звідки
Отже, закон розподілу ДВВ
7.Обчислимо
Подія Отже, Індивідуальні завдання 6 Виконати всі завдання 1-7, представлені в прикладі 1 для системи двох дискретних величин Практичне заняття № 7 Індивідуальні завдання 7 1. Випадкова величина 2. Два мисливці роблять по три постріли. Ймовірність влучення для кожного з них Зауваження. Ввести дві дискретні випадкові величини 3. Випадкова величина Тут Практичне заняття № 8 Індивідуальні завдання 8 Варіант 1. Серед дев’яти однотипних виробів п’ять відповідають вимогам стандарту, а решта – ні. Навмання береться шість виробів. Визначити закон розподілу цілочислової випадкової величини Х – появу числа виробів, що відповідають стандарту і обчислити для цієї величини Варіант 2. Під час штампування валиків імовірність відхилення кожного валика від стандартного розміру дорівнює 0,15. За робочу зміну робітником було проштамповано 800 валиків. Знайти закон Х – числа валиків, що не відповідають стандартному розміру, та її основні числові характеристики Варіант 3. У лабораторних умовах було висіяно 10000 насінин нового сорту ячменю. Імовірність того, що насінина ячменю не проросте в середньому становить 0,2. Визначити закон розподілу цілочислової випадкової величини Х – числа зернин ячменю, що проростуть, і обчислити Варіант 4. Радіотелефонна станція отримує цифровий текст. Унаслідок атмосферних завад імовірність спотворення цифри в середньому дорівнює 0,001. Було отримано текст, що налічує 2000 цифр. Знайти закон розподілу Х – числа спотворених цифр в отриманому тексті. Варіант 5. В урні міститься 100 кульок, із них 80 білі, а решта чорні. Кульки із урни виймають навздогад по одній із поверненням. Знайти закон розподілу Х – числа проведених експериментів, якщо вони здійснюються до першої появи чорної кульки. Чому дорівнюють Варіант 6. В електромережу містечка увімкнуто для освітлення вулиць у вечірню пору 20000 електрола
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1007; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.147.121 (0.014 с.) |

 .
. чисел, а всього чисел, які діляться на 3, буде
чисел, а всього чисел, які діляться на 3, буде 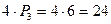 . Отже, події В сприяє 24 елементарні події.
. Отже, події В сприяє 24 елементарні події. .
. до
до  годин, а також про те, що той, хто прийде першим, чекатиме на другого протягом
годин, а також про те, що той, хто прийде першим, чекатиме на другого протягом  годин. Знайти ймовірність того, що зустріч відбудеться, якщо кожна особа може прийти в довільний момент часу
годин. Знайти ймовірність того, що зустріч відбудеться, якщо кожна особа може прийти в довільний момент часу  .
. – множина точок квадрата зі стороною
– множина точок квадрата зі стороною 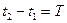 . Подіями доцільно вважати частини квадрата, що мають площу. Події А – „зустріч відбудеться” відповідає заштрихована частина квадрата, якщо момент приходу кожної особи –
. Подіями доцільно вважати частини квадрата, що мають площу. Події А – „зустріч відбудеться” відповідає заштрихована частина квадрата, якщо момент приходу кожної особи –  і
і  . Подія А відбудеться за умови
. Подія А відбудеться за умови 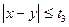 , де
, де 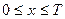 ,
,  .
. (рис.1). Часу Т відповідає площа квадрата ONCK, а події А площа шестикутника OEDCBA.
(рис.1). Часу Т відповідає площа квадрата ONCK, а події А площа шестикутника OEDCBA.
 .
. ) її координати. Знайти ймовірність того, що рівняння
) її координати. Знайти ймовірність того, що рівняння 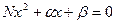 має дійсні корені (
має дійсні корені (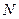 - номер варіанту).
- номер варіанту). фірм мали прибуток, акції N фірм знецінились, а акції k фірм – зберегли свою номінальну вартість. Яка ймовірність того, що випадково куплені k –1 акцій різних фірм матимуть прибуток?
фірм мали прибуток, акції N фірм знецінились, а акції k фірм – зберегли свою номінальну вартість. Яка ймовірність того, що випадково куплені k –1 акцій різних фірм матимуть прибуток? та
та  .
. , для другого –
, для другого – 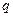 0,6, для третього -
0,6, для третього -  2/3. Визначити ймовірність своєчасної сплати податків: а) не більше ніж одним підприємством; б) лише одним підприємством; в) двома підприємствами; г) жодним підприємством; д) хоча б одним підприємством.
2/3. Визначити ймовірність своєчасної сплати податків: а) не більше ніж одним підприємством; б) лише одним підприємством; в) двома підприємствами; г) жодним підприємством; д) хоча б одним підприємством.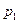 . У групі n студентів. Знайти найімовірнішу кількість членів цієї групи котрі складуть іспит, і обчислити відповідну імовірність.
. У групі n студентів. Знайти найімовірнішу кількість членів цієї групи котрі складуть іспит, і обчислити відповідну імовірність.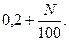 Знайти ймовірність того, що при
Знайти ймовірність того, що при  незалежних випробувань, відхилення відносної частоти появи події від її ймовірності по модулю не перевищить
незалежних випробувань, відхилення відносної частоти появи події від її ймовірності по модулю не перевищить 


 де
де  де
де 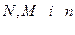 :
:











 Виконати завдання прикладу 4 (в п. 5 задачі обчислити ймовірність
Виконати завдання прикладу 4 (в п. 5 задачі обчислити ймовірність  ).
). задана таблицею розподілу.
задана таблицею розподілу. х y
х y








 і
і  та знайти одновимірні функції їх розподілів.
та знайти одновимірні функції їх розподілів. . Обчислити математичне сподівання цього розподілу.
. Обчислити математичне сподівання цього розподілу. та обчислити
та обчислити  .
. .
. , де
, де 
 звідки
звідки 
 :
:


 ;
;  .
.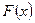 має вигляд:
має вигляд: 
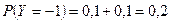 ;
;  ;
;  ;
;  .
.


 має вигляд:
має вигляд:







 де
де 


 то між ДВВ X та Y існує кореляційний зв'язок.
то між ДВВ X та Y існує кореляційний зв'язок. то цей кореляційний зв'язок має «відємний» характер: із зростанням однієї величини інша величина спадає.
то цей кореляційний зв'язок має «відємний» характер: із зростанням однієї величини інша величина спадає.
 то величина
то величина  свідчить про помірний зв'язок між X таY.
свідчить про помірний зв'язок між X таY. .
. , маємо
, маємо 


 .
.





 ми знайшли в пункті 2.
ми знайшли в пункті 2.





 ми знайшли в пункті 2.
ми знайшли в пункті 2. як добуток
як добуток  відповідних рядка і стовпця, перетин яких утворює ці клітини.
відповідних рядка і стовпця, перетин яких утворює ці клітини. y
x
y
x









 користуючись законом розподілу системи ДВВ
користуючись законом розподілу системи ДВВ 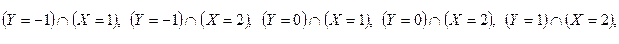 тоді
тоді 

 , заданої таблицею розподілу.
, заданої таблицею розподілу. Знайти щільність розподілу випадкової величини
Знайти щільність розподілу випадкової величини 
 Знайти закон розподілу випадкової величини
Знайти закон розподілу випадкової величини 
 - кількість влучень для першого та другого мисливців та розглянути
- кількість влучень для першого та другого мисливців та розглянути 
 Знайти закон розподілу випадкової величини
Знайти закон розподілу випадкової величини  обчислити
обчислити 
 - кількість літер у прізвищі;
- кількість літер у прізвищі; 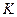 - кількість літер у повному імені.
- кількість літер у повному імені. .
.
 ?
?


