
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Елементарні множини та їх властивостіСодержание книги
Поиск на нашем сайте
Означення 3.1.1 Будь-які інтервали Означення 3.1.2 Елементарними множинами в Одже будь-яка елементарна множина Властивості елементарних множин. 1. Перетин скінченної множини елементарних множин є елементарна множина. Доведення. Твердження очевидно, якщо розглянути перетин двох відрізків. Розглянемо випадок двох множин Загальний випадок доводиться методом математичної індукції. 2. Доповнення елементарної множини Доведення. Твердження очевидно, якщо елементарна множина 3. Об’єднання скінченної множини елементарних множин є елементарна множина. Доведення. Розглянемо випадок двох множин 4. Різниця Доведення. Зобразимо різницю 5. Симетрична різниця Ця властивість випливає з 4 і 3, тому що
Міра елементарних множин та її властивість Означення 3.2.1 Мірою будь якого відрізка Тобто незалежно від того, чи буде відрізок Означення 3.2.2 Мірою будь якої елементарної множини Розглянемо наступні властивості. 1. Якщо множини Доведення. Позначимо
Методом математичної індукції ця властивість поширюється на випадок скінченної множини неперетинних елементарних множин. Ця властивість називається адитивністю міри.
Наслідок 1. Якщо
Доведення. Зобразимо множину Наслідок 2. Якщо
Ця властивість виливає з (3.2.1), тому що Наслідок 3. Якщо
Доведення. Зобразимо множину
Наслідок 4. Якщо елементарна множина
Доведення. Нехай
2. Якщо елементарна множина
Доведення. Нехай
і
Оскільки множина
Отже Наслідок 4. Якщо елементарна множина
Доведення. В силу (3.2.3)
|
|||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 247; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.74.100 (0.01 с.) |

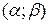 , півінтервали
, півінтервали 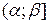 або
або 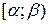 , або сегменти
, або сегменти 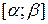 будемо називати відрізками і позначати літерой
будемо називати відрізками і позначати літерой  . При цьому у число відрізків включаємо порожню множину
. При цьому у число відрізків включаємо порожню множину 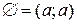 і сегмент, що складається з одної точки
і сегмент, що складається з одної точки 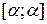 .
.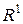 будемо називати будь-ялі скінченні об’єднання попарно неперетинних відрізків. Зокрема, будь-який відрізок – елементарна множина.
будемо називати будь-ялі скінченні об’єднання попарно неперетинних відрізків. Зокрема, будь-який відрізок – елементарна множина. має вигляд
має вигляд 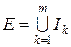 , де
, де 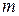 може бути довільним натуральним числом і відрізки
може бути довільним натуральним числом і відрізки 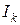 попарно не перетинаються.
попарно не перетинаються.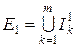 і
і 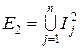 . Маємо
. Маємо 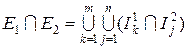 .
. .
.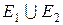 . Розглянемо доповнення множини
. Розглянемо доповнення множини 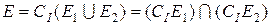 . Внаслідок властивостей 2 і 1 множина
. Внаслідок властивостей 2 і 1 множина 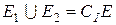 .
.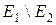 двох елементарних множин є елементарна множина.
двох елементарних множин є елементарна множина.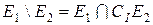 , де
, де  двох елементарних множин є елементарна множина.
двох елементарних множин є елементарна множина.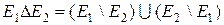 .
.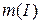 .
.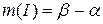 . Зокрема міра відрізку
. Зокрема міра відрізку 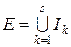 називається сума довжин відрізків
називається сума довжин відрізків  .
. і
і  .
.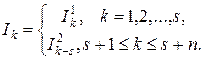 Тоді
Тоді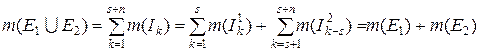 .
. і
і  - елементарні множини і
- елементарні множини і 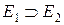 , то
, то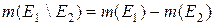 . (3.2.1)
. (3.2.1)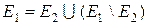 . В силу адитивності міри
. В силу адитивності міри 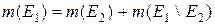 , а це еквівалентно сформулюваному.
, а це еквівалентно сформулюваному. .
. , і називається монотонністю міри.
, і називається монотонністю міри.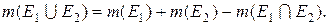 (3.2.2)
(3.2.2)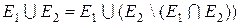 і далі застосуємо властивість 1 і наслідок 1:
і далі застосуємо властивість 1 і наслідок 1: .
.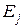 ,
, 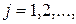 r, то
r, то .
.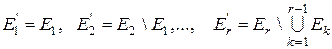 . Множини
. Множини 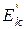 попарно не перетинаються і, як легко перевірити,
попарно не перетинаються і, як легко перевірити, 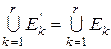 . Отже, внаслідок монотонності і адитивності одержимо
. Отже, внаслідок монотонності і адитивності одержимо .
. . (3.2.3)
. (3.2.3) . Для кожного відрізку
. Для кожного відрізку 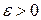 знайдемо сегмент
знайдемо сегмент 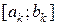 такий, що
такий, що  і
і 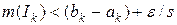 . З іншого боку для кожного відрізка
. З іншого боку для кожного відрізка  і
і  такий, що
такий, що 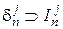 і
і  . Тоді
. Тоді (3.2.4)
(3.2.4)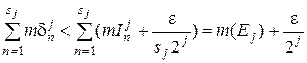 . (3.2.5)
. (3.2.5)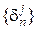 покриває замкнену обмежену множину
покриває замкнену обмежену множину  =
=  . За лемою Гейне-Бореля існує скінченне покриття, яке позначимо через
. За лемою Гейне-Бореля існує скінченне покриття, яке позначимо через 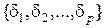 . Оскільки сегменти
. Оскільки сегменти 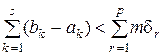 і внаслідок нерівностей (3.2.4-3.2.5) маємо
і внаслідок нерівностей (3.2.4-3.2.5) маємо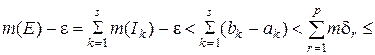
 .
. . Спрямувавши
. Спрямувавши  до нуля одержимо (3.2.3). Властивість 2 доведена.
до нуля одержимо (3.2.3). Властивість 2 доведена.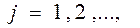 то
то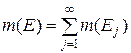 . (3.2.6)
. (3.2.6)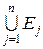 , де
, де  -довільне натуральне число, то внаслідок монотонності та адитивності міри
-довільне натуральне число, то внаслідок монотонності та адитивності міри 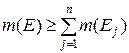 і отже
і отже 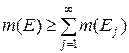 , що з раніш одержаною нерівністю
, що з раніш одержаною нерівністю 


