
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Множини потужності континуумуСодержание книги
Поиск на нашем сайте
Теорема 1.4.1 (Кантор). Множина точок сегмента Доведення. Припустимо, що це ні так, тобто сегмент Означення 1.4.1. Множина А має потужність континууму, або потужність с, якщо А ~ Приклади множин потужності континууму. 1. Тому що 2. Будь-який сегмент 3. Будь-який інтервал 4. Множина 5. Множина 6. Множина всіх трансцендентних чисел має потужність континууму, оскільки цю множину можливо зобразити як різницю між множиною 7. Множина 8. Очевидно, що піввісь
Властивості множин потужності континууму. 1. Об’єднання скінченної множини Доведення. Розглянемо півінтервали 2. Об’єднання зчисленної множини множин Доведення. Розглянемо півінтервали 3. Об’єднання не більш ніж зчисленної множини множин Доведення. Розглянемо випадок зчисленої множини множин Двійкові дроби. Означення 1.4.2. Двійковим дробом називається сума ряду Цей ряд збігається, сума його невід’ємна і не перевищує одиниці тому, що члени його мажоруються членами геометричної прогресії. Отже кожному двійковому дробу відповідає число – сума ряду Теорема 1.4.2. Кожному числу Доведення. Нехай Теорема доведена. Означення 1.4.3. Нехай В силу теореми 1.4.2
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 309; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.151.11 (0.006 с.) |

 не є зчисленною.
не є зчисленною. . Поділимо сегмент
. Поділимо сегмент  ,
,  і
і 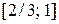 і позначимо через
і позначимо через  той з них, що не містить елемент
той з них, що не містить елемент  (якщо таких сегментів два, беремо будь-який з них). Поділимо сегмент
(якщо таких сегментів два, беремо будь-який з них). Поділимо сегмент 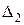 той з них, що не містить елемент
той з них, що не містить елемент  . І так далі, якщо вибрано сегмент
. І так далі, якщо вибрано сегмент 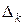 , поділимо сегмент
, поділимо сегмент  той з них, що не містить елемент
той з них, що не містить елемент  . Тепер зауважимо, що
. Тепер зауважимо, що  і довжина сегмента
і довжина сегмента  . Отже, внаслідок відомої теореми про вкладені сегменти, довжини яких прямують до нуля, існує елемент
. Отже, внаслідок відомої теореми про вкладені сегменти, довжини яких прямують до нуля, існує елемент 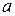 спільний всім сегментам
спільний всім сегментам  . З іншого боку існує
. З іншого боку існує 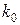 таке, що
таке, що  . Але, завдяки вибору сегментів
. Але, завдяки вибору сегментів 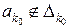 . Одержана суперечність доводить теорему.
. Одержана суперечність доводить теорему.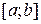 має потужність континууму, оскільки функція
має потужність континууму, оскільки функція 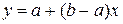 встановлює взаємно однозначну відповідність між множинами
встановлює взаємно однозначну відповідність між множинами  , будь-який півінтервал
, будь-який півінтервал  або
або  має потужність континууму. Дійсно, завдяки властивості 4 потужності, вилучення одного або двох елементів з нескінченної множини не міняє потужності.
має потужність континууму. Дійсно, завдяки властивості 4 потужності, вилучення одного або двох елементів з нескінченної множини не міняє потужності.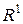 - всіх дійсних чисел має потужність континууму, оскільки функція
- всіх дійсних чисел має потужність континууму, оскільки функція 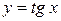 встановлює взаємно однозначну відповідність між множинами
встановлює взаємно однозначну відповідність між множинами 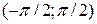 і
і  всіх ірраціональних чисел має потужність континууму, тому що множину
всіх ірраціональних чисел має потужність континууму, тому що множину  можливо зобразити як різницю між множиною
можливо зобразити як різницю між множиною 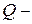 всіх раціональних чисел. Отже, завдяки властивості 4 потужності, вилучення зчисленної множини не міняє потужності.
всіх раціональних чисел. Отже, завдяки властивості 4 потужності, вилучення зчисленної множини не міняє потужності. - всіх додатних чисел має потужність континууму, тому що функція
- всіх додатних чисел має потужність континууму, тому що функція  встановлює взаємно однозначну відповідність між множинами
встановлює взаємно однозначну відповідність між множинами  і
і  має потужність с.
має потужність с. множин
множин 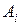 потужності континууму, які попарно не мають спільних елементів, є множиною потужності континууму.
потужності континууму, які попарно не мають спільних елементів, є множиною потужності континууму. Вони попарно не мають спільних елементів і
Вони попарно не мають спільних елементів і  ~
~  ~
~  . Властивість доведена.
. Властивість доведена. потужності, які попарно не мають спільних елементів, є множиною потужності с.
потужності, які попарно не мають спільних елементів, є множиною потужності с. . Вони попарно не мають спільних елементів і
. Вони попарно не мають спільних елементів і  ~
~  . Властивість доведена.
. Властивість доведена. взаємно однозначна відповідність множини
взаємно однозначна відповідність множини  . Множини
. Множини  попарно не мають спільних елементів і
попарно не мають спільних елементів і  . Оскільки
. Оскільки  , то завдяки властивості 4 еквівалентних множин,
, то завдяки властивості 4 еквівалентних множин,  ~
~ 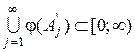 . З іншого боку
. З іншого боку  . За теоремою Кантора-Бернштейна
. За теоремою Кантора-Бернштейна  . Властивість доведена.
. Властивість доведена. , де
, де 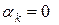 або 1.
або 1. і також називати двійковим дробом. Двійковий дріб виду
і також називати двійковим дробом. Двійковий дріб виду  , де
, де 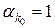 , називається двійково-раціональним числом. Ця сума дорівнює раціональному числу
, називається двійково-раціональним числом. Ця сума дорівнює раціональному числу  , де m непарне число менше за
, де m непарне число менше за 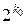 . Двійково-раціональне число
. Двійково-раціональне число  (запис (0) («0 в періоді») означає, що усі
(запис (0) («0 в періоді») означає, що усі  якщо
якщо  ) має зображення
) має зображення  .
.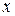 з інтервала (0; 1), що не є двійково-раціональним числом, відповідає єдиний двійковий дріб.
з інтервала (0; 1), що не є двійково-раціональним числом, відповідає єдиний двійковий дріб. і не є двійково-раціональним числом. Необхідно побудувати
і не є двійково-раціональним числом. Необхідно побудувати  для будь-якого
для будь-якого  і довести, що частинна сума
і довести, що частинна сума 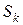 ряду
ряду 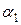 . Якщо
. Якщо  , покладемо
, покладемо  . Тоді
. Тоді  і
і  . Якщо
. Якщо  , то покладемо
, то покладемо  . Тоді
. Тоді  і
і  ,
, 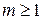 такі, що
такі, що  . Знову розглянемо два випадки. Якщо
. Знову розглянемо два випадки. Якщо  , то покладемо
, то покладемо  .
. 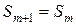 і
і  . Якщо
. Якщо  , то покладемо
, то покладемо  . Тоді
. Тоді 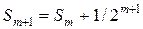 і
і  . Число
. Число  , тому що
, тому що 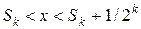 . З останній нерівності випливає
. З останній нерівності випливає  .
. множина всіх двійкових дробів,
множина всіх двійкових дробів,  множина усіх двійкових дробів, зображення яких містить нескінченну множину чисел
множина усіх двійкових дробів, зображення яких містить нескінченну множину чисел  множина всіх двійкових дробів, зображення яких містить одиницю в періоді.
множина всіх двійкових дробів, зображення яких містить одиницю в періоді. має потужність континуум, а множина
має потужність континуум, а множина  - множина потужності континууму.
- множина потужності континууму.


