
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Зчислені множини та їх властивостіСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Означення 1.3.1. Множини А називається зчисленною, або множиною зчисленної потужності, якщо вона еквівалентна множині натуральних чисел Теорема 1.3.1 (Критерій зчисленості множини). Щоб множина А була зчисленною, необхідно і досить, щоб її можно було зображити у вигляді послідовності: Доведення. Необхідність. Нехай Достатність. Нехай Загальні властивості потужності множин. 1. Будь яка нескінченна множина А має потужність не меншу зчисленної потужності, тобто Доведення. Виберемо будь який елемент в множині А і позначимо його через 2. Об’єднання зчисленної множини Доведення. Спочатку в рядок запишемо елементи множини 3. Об’єднання нескінченної множини А і скінченної або зчисленної множини В еквівалентно множині А. Доведення. Виділимо з множини 4. Якщо різниця множини Доведення. Перетин 5. Об’єднання зчисленної множини скінченних множин
Доведення. Спочатку в рядок запишемо елементи множини 6. Об’єднання скінченної множини зчисленних множин Доведення. Кожну множину 7. Об’єднання зчисленної множини зчисленних множин Доведення. Множину 8. Якщо елементи множини А визначаються m значками, тобто Доведення. Застосуємо метод математично індукції. Якщо елементи множини Приклади зчисленних множин. 1. Множина - усіх натуральних чисел зчисленна, тому що 2. Будь-яка нескінченна підмножина натуральних чисел зчисленна, тому що її можливо зобразити у вигляді 3. Множина 4. Множина 5. Множина 6. Множина A={
Дійсно елементи множини A визначаються 7. Множина Дійсно кожен елемент 8. Множина Множину 9. Множина Позначимо через
|
||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 658; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.0.34 (0.011 с.) |

 . Зчисленну потужність множини будемо позначати літерою
. Зчисленну потужність множини будемо позначати літерою 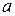 . Тобто запис
. Тобто запис 
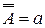 означає, що множини А зчисленна.
означає, що множини А зчисленна.
 ~
~  позначимо через
позначимо через 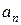 . Тим самим визначено загальний член послідовності. Отже:
. Тим самим визначено загальний член послідовності. Отже: 
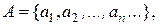 де всі елементи послідовності різні. Кожному елементу
де всі елементи послідовності різні. Кожному елементу  . Оскільки різні елементи мають різні номери і кожне натуральне число
. Оскільки різні елементи мають різні номери і кожне натуральне число 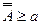 .
. . Оскільки різниця
. Оскільки різниця 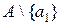 теж нескінченна, виберемо із неї будь який елемент і позначимо його через
теж нескінченна, виберемо із неї будь який елемент і позначимо його через  . Припустимо, що вже вибрано елементи
. Припустимо, що вже вибрано елементи  , …,
, …,  . Різниця
. Різниця  - нескінченна. Тому із неї можливо вибрати елемент
- нескінченна. Тому із неї можливо вибрати елемент  , де m - довільне натуральне число. Отже з множини А виділина підмножина
, де m - довільне натуральне число. Отже з множини А виділина підмножина 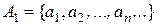 зчисленної потужності. А це означає, що
зчисленної потужності. А це означає, що 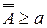 .
.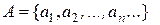 і скінченної множини
і скінченної множини 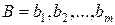 еквівалентно множині А, отже
еквівалентно множині А, отже 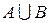 - зчисленна множина.
- зчисленна множина. , а потім будемо виписувати елементи множини А, пропускаючи ті елементи, що належать також множині
, а потім будемо виписувати елементи множини А, пропускаючи ті елементи, що належать також множині  і нехай D – різниця множин
і нехай D – різниця множин  і
і  . Оскільки
. Оскільки  ~
~ 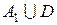 , то внаслідок властивості 3 еквівалентних множин
, то внаслідок властивості 3 еквівалентних множин 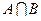 скінченна або зчисленна множина. Отже, за попередньої властивістю внаслідок рівності
скінченна або зчисленна множина. Отже, за попередньої властивістю внаслідок рівності  одержимо властивість 4.
одержимо властивість 4. - зчисленна або скінченна множина.
- зчисленна або скінченна множина. , пропускаючи ті елементи, що уже вибрані.
, пропускаючи ті елементи, що уже вибрані.  буде зображена у вигляді рядка або послідовності, отже вона скінченна або зчисленна.
буде зображена у вигляді рядка або послідовності, отже вона скінченна або зчисленна. - зчисленна множина.
- зчисленна множина.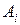 зобразимо у виглядіпослідовності
зобразимо у виглядіпослідовності  , а потім будемо виписувати елементи множин
, а потім будемо виписувати елементи множин 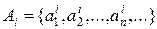 . Першим в рядок поставимо елемент
. Першим в рядок поставимо елемент 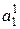 , а потім запишемо елементи у яких сума верхнього і нижнього індексів дорівнює трьом, чотирьом і так далі. При цьому будемо виписувати елементи множин
, а потім запишемо елементи у яких сума верхнього і нижнього індексів дорівнює трьом, чотирьом і так далі. При цьому будемо виписувати елементи множин  , кожен з яких приймає зчисленну кількість значень
, кожен з яких приймає зчисленну кількість значень 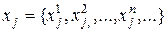 ,
,  то А - зчисленна.
то А - зчисленна.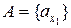 визначаються одним значком, значення якого
визначаються одним значком, значення якого 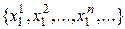 , то множину А можливо зобразити у вигляді
, то множину А можливо зобразити у вигляді 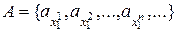 . Отже А - зчисленна. Нехай властивість 8 має місце для k індексів (
. Отже А - зчисленна. Нехай властивість 8 має місце для k індексів (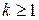 ). Розглянемо множину
). Розглянемо множину  і її підмножину
і її підмножину  елементів, у яких k+1індекс має фіксоване довільне значення
елементів, у яких k+1індекс має фіксоване довільне значення  . В силу припущення, кожна множина
. В силу припущення, кожна множина  - зчисленна, а тоді зчисленна множина А тому, що
- зчисленна, а тоді зчисленна множина А тому, що  . Отже, за принципом математичної індукції властивість 8 має місце для будь якого m.
. Отже, за принципом математичної індукції властивість 8 має місце для будь якого m. .
. усіх додатних раціональних чисел зчисленна.
усіх додатних раціональних чисел зчисленна.  можливо зобразити у вигляді
можливо зобразити у вигляді 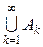 , де
, де  - множина раціональних чисел вигляду
- множина раціональних чисел вигляду  . Оскільки кожна множина
. Оскільки кожна множина  є зчисленною.
є зчисленною.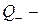 усіх від’ємних раціональних чисел зчисленна, оскільки
усіх від’ємних раціональних чисел зчисленна, оскільки  .
.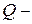 усіх раціональних чисел зчисленна, завдяки тому, що
усіх раціональних чисел зчисленна, завдяки тому, що 
 -усіх точек к-вимірного евклідового простору
-усіх точек к-вимірного евклідового простору  , координати яких раціональні числа, - зчисленна.
, координати яких раціональні числа, - зчисленна. значками (координатами точки), кожен з яких приймає зчисленну множину значень. Отже, внаслідок властивості 8, множина A - зчисленна.
значками (координатами точки), кожен з яких приймає зчисленну множину значень. Отже, внаслідок властивості 8, множина A - зчисленна.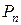 всіх алгебраїчних многочленів степеня не вище n з раціональними коефіцієнтами зчисленна.
всіх алгебраїчних многочленів степеня не вище n з раціональними коефіцієнтами зчисленна. множини
множини  раціональними коефіцієнтами:
раціональними коефіцієнтами:  . Отже, завдяки властивості 8, множина
. Отже, завдяки властивості 8, множина 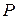 всіх алгебраїчних многочленів з раціональними коефіцієнтами зчисленна.
всіх алгебраїчних многочленів з раціональними коефіцієнтами зчисленна.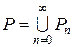 . Тому, завдяки властивості 7, множина
. Тому, завдяки властивості 7, множина 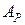 всіх алгебраїчних чисел - зчисленна.
всіх алгебраїчних чисел - зчисленна. множину алгебраїчних чисел, що відповідають алгебраїчному многочлену
множину алгебраїчних чисел, що відповідають алгебраїчному многочлену  , то внаслідок властивості 5,
, то внаслідок властивості 5, 


