
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні означення теорії множин.Содержание книги
Поиск на нашем сайте Множина – це будь-яке об’єднання відмінних та визначених об’єктів нашої інтуїції або інтелекту, яке розглядається як єдине ціле. Множина – це сукупність об’єктів, об’єднаних за певною ознакою. Приклади: - множина букв алфавіту; - множина точок на прямій; - множина двозначних натуральних чисел; - множина цілих чисел і т.д. Множини позначають А, В, С, … Об’єкти з яких складається множина називаються її елементами: а, в, с, … Якщо елемент а належить множині А, то позначають: Якщо елементами множини є числа, то її називають числовою: - множина натуральних чисел: N - множина цілих чисел: Z - множина раціональних чисел: Q - множина дійсних чисел: R Множина називається скінченною, якщо вона має скінченну кількість елементів. Множина називається нескінченною, якщо вона має нескінченну кількість елементів. Кількість елементів множини називається потужністю: Множина яка не має жодного елемента називається порожньою: Æ Множина А називається підмножиною множини В тоді і лише тоді, коли будь – який елемент множини А належить множині В: Будь – яка множина є підмножиною самої себе. Порожня множина є підмножиною будь – якої множини. Тому у будь – якої множини є дві очевидних підмножини: порожня і сама ця множина. Приклад: Множина всіх підмножин множини А називається булеаном множини А і позначається: В (А). Теорема: кожна множина А, яка містить п елементів, має 2п підмножин.
Теорема: порожня множина є підмножиною будь – якої множини. Нехай дано дві множини: А і Æ. Доведемо, що Æ Припустимо, що твердження Æ
Дві множини А і В називаються рівними, коли кожний елемент множини А є елементом множини В і навпаки: Властивості множин: § рефлективність: § симетричність: § транзитивність: Способи задання множин: Множина вважається заданою, якщо про будь – який об’єкт можна сказати чи належить він до даної множини чи ні. 1. Довільну скінченну множину можна задати переліком усіх її елементів. Наприклад: - множину студентів групи можна задати їх списком у журналі; - С={червень, липень, серпень} – множина літніх місяців. Спосіб задання множини переліком її елементів доцільно використовувати коли ця кількість не дуже велика. Так, множину всіх натуральних чисел, які менші 100000, можна задати переліком її елементів, але це займе дуже багато часу. У таких випадках використовують слідуючий запис: В={1; 2; 3; …; 99998; 99999}. Знак … можна використовувати тоді, коли зрозуміло, які елементи вони замінюють. 2. Задання множин за допомогою характеристичної властивості. Нескінченні множини неможливо задати переліком елементів, тому їх задають за допомогою характеристичної властивості Означення. Ознака або властивість, якою володіють усі елементи даної множини і не володіють елементи, що не належать до даної множини, називається характеристичною властивістю для даної множини. Характеристична властивість повинна бути такою, щоб було зрозуміло, чи належить даний об’єкт до множини, що розглядається. Для множин, які задаються характеристичною властивістю їх елементів, використовують запис: Приклади: 1) 2) 3) 2. Дії над множинами.
1. Об’єднанням множин А і В називається множина, яка складається з усіх тих і тільки тих елементів, які належать хоча б одній з множин А або В. Позначається: Об’єднання множин можна виконувати з будь – якою кількістю множин: Для об’єднання множин справедливі слідуючи властивості: 1) комутативна: 2) асоціативна: 3) 4) ідемпотентність: 5) Діаграми (круги) Ейлера – Венна - це графічне зображення множин. (Д. Венн – англійський математик, 1834-1932р.р. Л. Ейлер – швейцарський математик, 1707-1783р.р.)
Приклад:
2. Перетином множин А і В називається множина, яка складається з усіх тих і тільки тих елементів, які належать як множині А так і множині В (спільні елементи множин). Позначається: Дві множини А і В називаються непересічними, якщо Дві множини А і В називаються пересічними, якщо Перетин множин можна виконувати з будь – якою кількістю множин: Для перетину множин справедливі слідуючи властивості: 1) комутативна: 2) асоціативна: 3) 4) ідемпотентність: 5) Приклад:
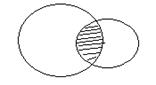
3. Різницею множин А і В називається множина, яка складається з тих і тільки тих елементів, які належать множині А і не належать множині В. Позначається:
Множина
Приклад: 4. Універсальна множина – це найбільша множина U, для якої вся решта множин є підмножинами. На діаграмах Ейлера – Венна універсальну множину позначають прямокутником:
Для універсальних множин справедливі слідуючи співвідношення: 5. Доповненням множини А до універсальної множини U називається така множина, що визначається співвідношенням Позначається: Множини За допомогою доповнення множин можна також у зручному вигляді подати різницю множин Теорема: Доведення: так як
Алгебра множин. Алгебра множин являє собою сукупність тотожностей (рівностей). Для будь – яких підмножин А, В і С універсальної множини U дійсними є такі рівності: 1) 2) 3) 4) 5)
1’) 2’) 3’) 4’) 5’) Кожну з наведених рівностей можна довести, показавши, що множина, яка стоїть з одного боку знака рівності, включена до множини, що стоїть з іншого боку від цього знака рівності. Доведемо рівність 3: Доведення складається з двох частин: 1) Нехай а) якщо б) якщо 2) Нехай У загальному вигляді рівності 3 і 3’ можна подати у такому вигляді:
Для довільних підмножин А, В універсальної множини U справедливі такі рівності: 1) якщо 2) 3) 4) 5) 6) 7) якщо 1’) якщо 2’) 3’) 4’) 5’) 6’) 7’) якщо Рівність алгебри множин, отримана з іншої рівності через заміну всіх входжень Для будь – якого істинного твердження, що формується в термінах двоїсте по відношенню до цього речення є також істинним. З цього випливає, що якщо є деяке твердження 1 – 7, то відповідне йому твердження 1’ – 7’ випливає на підставі двоїстості. Це дозволяє спрощувати різні складні вирази алгебри множин. Узагальнення операцій над множинами: 1) перетин множин: 2) об’єднання множин: 3) формули де Моргана: Контрольні запитання. 1. Що таке множина? Наведіть приклади різних множин. 2. Що таке скінченна та нескінченна множини? Наведіть приклади. 3. Яка множина називається порожньою? 4. Що таке підмножина? 5. Які є способи задання множин? 6. Що називається потужністю множини? 7. Що називається булеаном множини? 8. Що називається об’єднанням множин? (*) 9. Що називається об’єднанням множин? (*) 10. Що називається перерізом множин? (*) 11. Що називається різницею множин? (*) 12. Сформулювати і записати закони алгебри множин. (**)
Література: О.А. Борисенко. Лекції з дискретної математики: навчальний посібник для вузів. Суми, СумДУ, 1999р. лекції 2 - 4 Ю.В. Нікольський, В.В.Пасічник, Ю.М. Щербина. Дискретна математика. Підручник для вищих навчальних закладів. Київ. 2007р. розділ 1. п. 1.12 – 1.13
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1576; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |


 . Якщо елемент d не належить множині А, то позначають:
. Якщо елемент d не належить множині А, то позначають:  .
.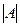
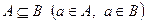 . Множина А, що строго включена до В, позначається так:
. Множина А, що строго включена до В, позначається так:  , це означає, що множина В містить і інші елементи крім елементів множини А.
, це означає, що множина В містить і інші елементи крім елементів множини А. . Підмножини множини А:
. Підмножини множини А:  Æ.
Æ. {
{ 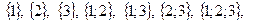 Æ}
Æ} .
. ,
, 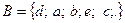

 ;
; ;
;
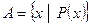 , де
, де  - скорочене позначення речення «елемент х має властивість Р»
- скорочене позначення речення «елемент х має властивість Р»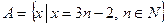 - множина натуральних чисел, що при діленні на 3 дають остачу 1.
- множина натуральних чисел, що при діленні на 3 дають остачу 1. - множина всіх раціональних коренів рівняння.
- множина всіх раціональних коренів рівняння. - множина натуральних чисел між числами 5 і 10.
- множина натуральних чисел між числами 5 і 10.

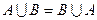

 Æ= А
Æ= А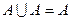
 тоді і тільки тоді, коли
тоді і тільки тоді, коли 
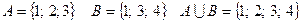
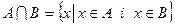
 Æ.
Æ.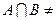 Æ.
Æ.


 Æ=Æ
Æ=Æ
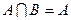 тоді і тільки тоді, коли
тоді і тільки тоді, коли 
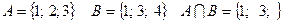



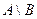

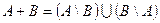



 ,
, 


 і
і  не мають спільних елементів, тому
не мають спільних елементів, тому  Æ,
Æ, 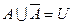 . Очевидно, що множина А є доповненням до
. Очевидно, що множина А є доповненням до  .
.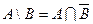
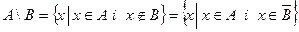 , то
, то  - дистрибутивний закон
- дистрибутивний закон
 - дистрибутивний закон
- дистрибутивний закон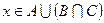 , тоді
, тоді  або
або 
 і
і  , а отже
, а отже 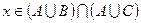
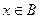 і
і  , а отже
, а отже 

 і
і  , то В =Æ.
, то В =Æ. - закон поглинання
- закон поглинання - закон де Моргана
- закон де Моргана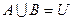 і
і 
 .
.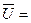 Æ
Æ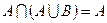 - закон поглинання
- закон поглинання - закон де Моргана
- закон де Моргана ,
,  ,
,  на Æ, Æ на
на Æ, Æ на  та Æ
та Æ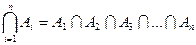 при
при  ;
; при
при  ,
,  .
.


