
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
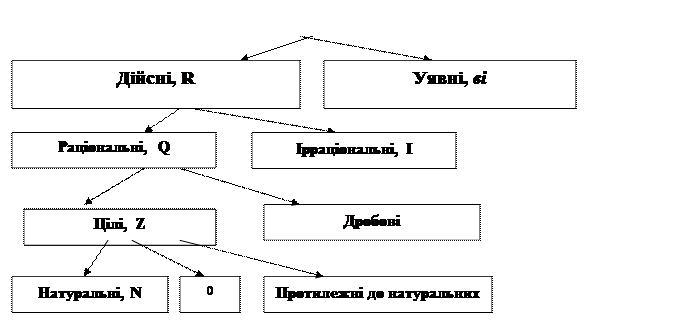
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
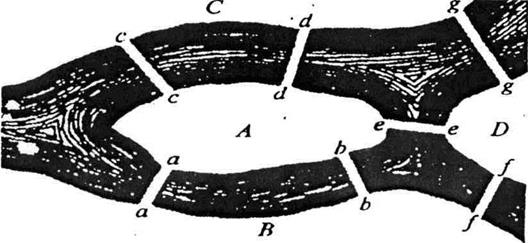
Якщо вийти з деякої частини міста, то Чи можна пройти кожен міст один раз і повернутися В початкову частину міста.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Обходу мостів відповідає послідовність ребер графа задачі, в якій два сусідні ребра мають спільну вершину, тобто маршрут. Так як в кінці обходу треба повернутися в початкову вершину міста і на кожному мості побувати один раз, то цей маршрут є циклом, що містить усі ребра графа.
Можна сказати, що Ейлерові графи це такі графи, які можна зобразити одним розчерком пера, при чому процес його зображення починається і закінчується в тій самій точці. Леонард Ейлер розв’язав цю задачу. Теорема Ейлера: скінчений неорієнтований граф є Ейлеровим тоді і тільки тоді, коли він зв’язний і степені всіх його вершин парні. Граф називається зв’язним, якщо будь – які дві вершини з’єднані маршрутом. Будь – який не зв’язний граф складається з кількох частин, кожна з яких є зв’язним графом. Ці частини називаються компонентами зв’язності графа. Дві вершини називаються зв’язними, якщо існує маршрут з кінцями в цих вершинах. У даній задачі вершини А, В, С, Д мають непарні степені, тому розв’язання задачі неможливе.
5. Дерево. Зв’язний граф без циклів називається деревом. «Зв’язний» означає, що його не можна розбити на два не розірвавши в якій–небудь вершині. З прикладами дерев ви зустрічаєтесь при роботі в NORTON COMMANDER – дерево каталогів, що будується за допомогою клавіш Ctrl +T. Теорема: граф є деревом тоді і тільки тоді, коли будь-які дві вершини сполучені рівно одним простим шляхом. Вершина графа з якої виходить рівно одне ребро, називається «висячою». Оскільки у графа кількість вершин скінчена, то така подорож обов’язково закінчиться, а закінчитись вона може лише у «висячій» вершині. Лема про «висячу» вершину: кожне дерево, яке має не менше двох вершин, має хоча б дві «висячі» вершини. Теорема: в дереві кількість вершин на одну більше за кількість ребер. m=n-1, де m - вершини, n - ребра.

Сукупність вершин, які знаходяться на відстані k ребер від кореня називаються k - ярусом дерева.
Бінарним (орієнтованим) деревом називається дерево, яке задовольняє умовам: а) в кореневу вершину не входить ні одна дуга; б) будь-яка інша вершина має тільки одну дугу, яка входить в неї і тільки або дві, або жодної дуги, яка виходить з неї.
Приклади. Множина чотирикутників зображена у вигляді дерева.

Множина чисел зображена у вигляді дерева.
Дерево розбору арифметичного виразу:
Транспортні мережі. Транспортною мережею називається скінчений граф без петель, який задовольняє умови: § існує лише одна вершина § існує лише одна вершина § кожному ребру (дузі) З поняттям транспортної мережі пов’язують поняття потоку. Нехай Потоком по дузі транспортної мережі називається функція 1) 2) Функцію
До аналізу транспортної мережі зводяться задачі, які виникають в процесі планування поставок матеріалів, розподілу потоків речовини, енергії, товарів між споживачами.
Нехай А – деяка множина вершин транспортної мережі ( Оскільки кожна частина речовини, що рухається від
Пропускна здатність розрізу А ( Задача про найбільший потік: при заданій конфігурації транспортної мережі та відомій пропускній здатності ребер необхідно знайти найбільше значення потоку, який може пропустити транспортна мережа, а також розподіл цього потоку по ребрах мережі. Дуга Повний потік – це такий потік Алгоритм для знаходження потоку був запропонований Фордом та Фалкерсоном і полягає в поступовому збільшенні потоку Знаходження найбільшого потоку складається з двох етапів. I етап. Знаходження повного потоку: нехай II етап. Знаходження найбільшого потоку. Нехай 1) проводимо розподіл потоку 2) приписування індексів вершинам: вершині
ненасичена дуга
ненасичена дуга
Приклад.
Контрольні запитання.
1. Основні поняття теорії графів. 2. Види графів. 3. Способи задання графів.(*) 4. Означення маршрута, ланцюга, цикла. 5. Означення дерева, бінарного дерева, приклади. (*) 6. Ейлерів граф. 7. Транспортні мережі: пропускна здатність ребра, поняття потоку. (**) 8. Задача про найбільший потік, алгоритм її ров’язання. (***)
Література: Ю.В. Нікольський, В.В.Пасічник, Ю.М. Щербина. Дискретна математика. Підручник для вищих навчальних закладів. Київ. 2007р. розділ 3. п. 3.1 – 3.9
Розділ 6. Теорія алгоритмів.
План. 1. Поняття алгоритму. 2. Основні вимоги до алгоритмів 3. Властивості алгоритмів. 4. Машина Тьюринга.
Поняття алгоритму.
Поняття алгоритму одне з найголовніших в математиці. З давніх часів у математиці склалось інтуїтивне уявлення про алгоритм, як формальне розпорядження, що визначає сукупність операцій і порядок їх виконання для розв’язання задач деякого типу. Термін походить від латинізованої вимови (Algorithmi) імені середньовічного узбецького математика аль – Хорезмі, який ще в 9 ст. сформулював правила, що дають змогу складати та розв’язувати квадратні рівняння. Процес розвитку обчислювальних методів сприяв ствердженню думки про те, що розв’язок будь – якої математичної проблеми має бути алгоритмічним. У техніку термін «алгоритм» введено разом із терміном «кібернетика». В зв’язку з цим знадобилось усвідомити, які вимоги має задовольняти послідовність дій (або її опис), щоб мати право називатися «алгоритмом». У цьому велику допомогу надала практика використання обчислювальних машин.
Процес розв’язування задачі на ЕОМ складається з таких етапів: 1) чітке формулювання задачі із зазначенням мети, яку потрібно досягти, тут виділяють початкові дані, результати і визначається зв’язок між ними; 2) визначення математичних співвідношень (формул, рівнянь, …), що пов’язують результати з початковими даними; 3) побудова схеми цього процесу (набір інструкцій); 4) запис алгоритму розв’язання задачі мовою, зрозумілою для ЕОМ; 5) пошук помилок у програмі та усунення їх; 6) розрахунки за готовою програмою та аналіз одержаних результатів. У різних задачах деякі з цих етапів можуть бути відсутні, деякі з цих етапів можуть бути поділені на більше число, але схема залишається такою ж.
Алгоритм – це сукупність правил, які визначають процедуру розв’язування будь – якої задачі з деякого класу задач.
Алгоритм – це програма, а критерій алгоритмічностіпроцесу є можливість запрограмувати його.
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 432; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.152.146 (0.009 с.) |










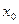 , яка називається входом (джерелом) мережі;
, яка називається входом (джерелом) мережі; , яка називається виходом (витоком) мережі;
, яка називається виходом (витоком) мережі; приписується число
приписується число 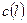 , яке називається пропускною здатністю ребра
, яке називається пропускною здатністю ребра 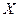 - довільна вершина транспортної мережі. Позначимо через
- довільна вершина транспортної мережі. Позначимо через 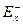 - множину всіх дуг, що заходять в дану вершину, а через
- множину всіх дуг, що заходять в дану вершину, а через 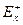 - множину всіх дуг, що виходять з даної вершини.
- множину всіх дуг, що виходять з даної вершини. , яка задовольняє умовам:
, яка задовольняє умовам: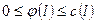
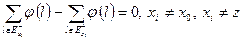

 від вершини
від вершини  . Згідно умови 1 ця кількість не може перевищувати пропускної здатності ребра. Згідно умови 2 потік, який заходить в вершину
. Згідно умови 1 ця кількість не може перевищувати пропускної здатності ребра. Згідно умови 2 потік, який заходить в вершину  - величина потоку транспортної мережі.
- величина потоку транспортної мережі.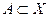 ), яка задовольняє умовам:
), яка задовольняє умовам: 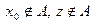 .позначимо
.позначимо  і
і 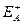 - множини ребер, які відповідно входять і виходять в вершини, які належать множині А. Повну сукупність
- множини ребер, які відповідно входять і виходять в вершини, які належать множині А. Повну сукупність  називають розрізом транспортної мережі.
називають розрізом транспортної мережі.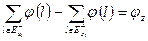
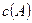 ) – це сума пропускних здатностей дуг, що заходять в вершини розрізу:
) – це сума пропускних здатностей дуг, що заходять в вершини розрізу: 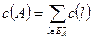 ,
, 
 .
. , кожний шлях якого від
, кожний шлях якого від  до тих пір, поки він не стане найбільшим.
до тих пір, поки він не стане найбільшим.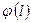 - деякий розподіл потоків по дугам транспортної мережі (його задають). Шукаємо шляхи
- деякий розподіл потоків по дугам транспортної мережі (його задають). Шукаємо шляхи  , які містять всі ненасичені дуги і припускаємо, що
, які містять всі ненасичені дуги і припускаємо, що 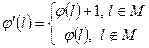
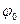 - повний потік.
- повний потік. ), всім іншим вершинам індекси приписуються так:
), всім іншим вершинам індекси приписуються так: а) якщо
а) якщо 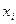 - має індекс
- має індекс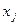 то j -тій вершині приписується індекс
то j -тій вершині приписується індекс 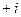
 б) якщо
б) якщо 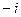

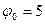 ,
, 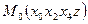

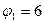 ,
, 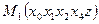
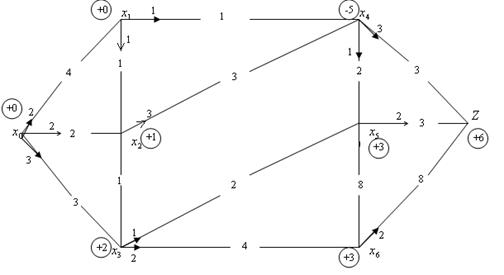
 - найбільший потік.
- найбільший потік.


