Поділ відрізків і кутів на рівні частини

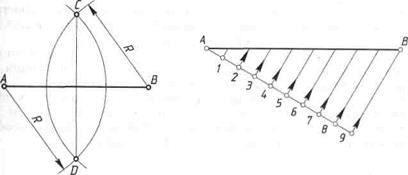
Поділ відрізків на рівні частини. Багато предметів мають однакові елементи, рівномірно розташовані уздовж прямої. Тому виникає необхідність на кресленнях ділити відрізки прямих на рівні частини. Найпростіше це робити за допомо­гою лінійки з нанесеною на ній міліметровою шкалою. Але при такому поділі іноді виникають незручності. Нехай відрі­зок довжиною 47 мм потрібно поділити на 9 рівних частин або відрізок, що становить 19 мм, — на 2 частини. Як тут бу­ти? Ось чому доцільніше застосовувати графічний метод — коли операція поділу виконується за допомогою циркуля і лінійки.

Поділ відрізка прямої на дві рівні частини. З обох кінців А і В заданого відрізка розхилом циркуля R, трохи більшим, ніж половина його довжини, описують дві дуги (рис. 22). Одержані у місцях перетину дуг точки С і D з'єднують між собою. Пряма, що з'єднала точки С і D, ділить відрізок АВ на дві рівні частини і перпендикулярна до нього.

Рис. 22. Поділ відрізка прямої на дві рівні частини за допомогою циркуля

Рис. 23. Поділ відрізка прямої на довільне число рівних частин

Поділ відрізка прямої на довільніу кількість рівних частин. З будь-якого кінця відрізка, наприклад з точки А, проводять підгострим кутом до нього допоміжну пряму. На ній циркулем або за допомогою лінійки відкладають потрібну кількість однакових відрізків довільної довжини (рис. 23). Останню точку з'єднують з другим кінцем заданого відрізка (з точкою В). З усіх точок по­ділу за допомогою лінійки і косинця проводять прямі, паралель­ні відрізку 9В (див.рис. 16). Ці прямі і поділяють відрізок АВ на задану кількість рівних частин.

Поділ кутів на рівні частини. Вивчаючи математику, ви ознайомились з поділом кутів на частини за допомогою тран­спортира. У кресленні існують прийоми поділу деяких кутів за допомогою циркуля.

Рис.24. Поділ кута на дві рівні частини за допомогою циркуля

Рис.24. Поділ кута на три рівні частини за допомогою циркуля

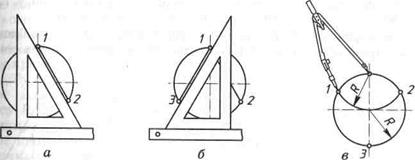
Поділ кута на дві рівні частини. З вершини кута опису­ють дугу кола довільного радіуса так, щоб вона перетнула сторони кута (рис. 24). З точок перетину М і N розхилом циркуля, трохи більшим, ніж половина дуги MN, описують дві дуги до їх перетину між собою. Одержану точку А і вер­шину О кута з'єднують прямою лінією — це і буде бісектри­са кута. Розглянутий прийом може бути застосований для по­ділу гострого, тупого чи прямого кута.

Поділ прямого кута на три рівні частини. З вершини ку­та описують дугу кола довільного радіуса R так, щоб вона пе­ретнула сторони кута (рис. 25). З точок перетину А і В тим же самим розхилом циркуля проводять допоміжні дуги до їх перетину з раніше проведеною дугою. Одержані точки М і N з'єднують прямими лініями з вершиною кута. Цим способом можна ділити на три рівні частини тільки прямі кути.

ЗАПИТАННЯ

1. У чому полягають недоліки поділу відрізків за допомогою лі­нійки з міліметровою шкалою?

2. Як графічно поділити відрізок прямої на дві рівні частини?

3. Як графічно поділити відрізок прямої на довільне число частин?

4. Чи можна графічно поділити на дві рівні частини прямий кут?

5. Чи можна графічно поділити на три рівні частини гострий кут?

Поділ кола на рівні частини

Поділ кола на три рівні частини. Для поділу потрібні лі­нійка й косинець з кутами 30°, 60°, 90°. Косинець більшим катетом встановлюють паралельно вертикальному діаметру кола (рис. 26, а). Вздовж гіпотенузи з точки 1 (перша поділ­ка, вона збігається з кінцем діаметра), проводять хорду і діс­тають другу поділку — точку 2. Перевернувши косинець і провівши другу хорду, дістають третю поділку — точку 3 (рис. 26, б). З'єднавши точки 2 і 3 відрізками прямої, діста­ють рівносторонній трикутник.

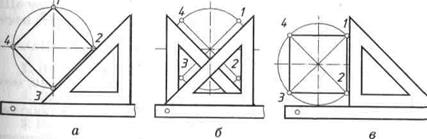
Рис. 26. Поділ кола на три рівні частини: а, б — за допомогою косинця і лінійки; в — циркулем

Ту саму задачу можна розв'язати за допомогою циркуля. Поставивши опорну ніжку циркуля у верхньому (чи нижньо­му) кінці вертикального діаметра (рис. 26, в), описують дугу радіусом, що дорівнює радіусу R кола. У місцях перетинупроведеної дуги з колом діста­ють точки 1 і 2 — першу і другу поділки. Третя поділка містить­ся на протилежному кінці діа­метра.

Поділ кола на чотири рівні частини. Щоб поділити коло на чотири рівні частини, треба про­вести два взаємно перпендику­лярних діаметри.

Два випадки таких побудов показано на рисунку 27. На ри­сунку 27, а діаметри проведено по лінійці та катету рівнобедреного косинця, а сторони вписаного квадрата — по його гіпотенузі. На рисунку 27, б і в навпаки, діаметри проведено по гіпотенузі косинця, а сторо­ни квадрата — по лінійці та катету косинця.

Рис. 27. Поділ кола на чотири рівні частини за допомогою косинця і лінійки

Рис. 28. Поділ кола на п'ять рівних частин за допомогою циркуля

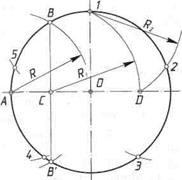
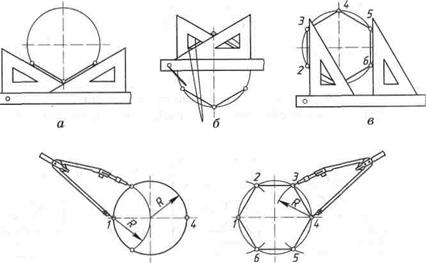
Поділ кола на п'ять рівних частин. Найпростіше цю за­дачу можна розв'язати за допомогою транспортира, послідов­но відкладаючи від одного з діаметрів центральні кути у 72° (тому що п'ятій частині кола відповідає такий кут).

За допомогою циркуля поділ виконують у такій послідов­ності (рис. 28). У кінці горизонтального діаметра ставлять точку А. Розхилом циркуля, що дорів­нює радіусу R кола, з точки А про­водять дугу до перетину з колом у точках В і В ¹. Ці точки з'єднують прямою лінією, яка перетинає го­ризонтальний діаметр у точці С. Це середина відрізка АО.

У верхньому кінці вертикально­го діаметра ставлять точку 1. Із точки С описують дугу радіусом R ₁ що дорівнює відстані між точками С і 1. У місці перетину цієї дуги з горизонтальним діаметром дістають точку D. З точки 1 як з центра описують третю дугу розхилом цирку­ля R ₂, що дорівнює відстані між точками 1 і D. У місці перети­ну цієї дуги з колом дістають точку 2. Точка 1 буде першою поділкою на колі, а точка 2 — другою. Відстань між точками 1 і 2 відкладають циркулем по колу і дістають точки З, 4 і 5.

Поділ кола на шість рівних частин. Поділ виконують за допомогою лінійки і косинця з кутами 30°, 60° і 90°. Для цього з кінцевих точок вертикального діаметра кола прово­дять відрізки по гіпотенузі косинця, прикладеного до лі­нійки більшим катетом (рис. 29, а, б). Закінчують побудо­ву проведенням вертикальних відрізків прямих (рис. 29, в).

Ту саму задачу можна розв'язати за допомогою цирку­ля. Для цього розхил циркуля встановлюють рівним раді­усу R кола. З протилежних кінців одного з діаметрів кола (наприклад, точок 1 і 4, рис. 29, г, д) описують дуги. Точ­ки перетину цих дуг з колом— точки 2, 3, 5, 6 разом з точками 1 і 4 ділять коло на шість рівних частин.

Рис. 29. Поділ кола на шість рівних частин: а, б, в — за допомогою косинця і лінійки; г, д — циркулем

Рис. 30. Поділ кола на вісім рівних частин за допомогою косинця і лінійки

Поділ кола на вісім рівних частин. Перші чотири точки поділу 1, 3, 5, 7 знаходяться на перетині центрових ліній з колом (рис. 30). їх проводять за допомогою лінійки та косинця. Ще чотири точки — 2, 4, 6, 8 знаходять за допомогою гіпоте­нузи рівнобедреного косинця, яка проходить через центр кола.

 

ЗАПИТАННЯ

1. На скільки рівних частин можна поділити коло за допомо­гою лінійки і косинців?

2. Яким косинцем слід скористатися для поділу кола на три частини? на шість частин? на вісім частин?

3. На скільки рівних частин можна поділити коло за допомогою Циркуля?

4. Чому дорівнює розхил циркуля при поділі кола на три рівні частини? на шість рівних частин?

КРЕСЛЕННЯ ПЛОСКИХ ПРЕДМЕТІВ