
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Мінімізація логічних функцій за допомогою таблиць Вейча.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Цифрові апарати для опису своєї роботи використовують логічні функції від п змінних F=F (x1, x2, …, xn). При цьому змінна хі може виявлятись більше одного разу. Тому число літер в запису логічної функції більше кількості змінних цієї функції. На практиці ставиться задача зменшення числа літер до мінімального значення – це задача мінімізації логічних функцій. Універсальним методом мінімізації логічних функцій є метод Квайна, який придатний для функцій будь-якого числа змінних. Він зручний для реалізації в ЕОМ в алгоритмічній формі. На практиці ставиться задача мінімізації функцій вручну для невеликого числа змінних. З цією метою були розроблені методи мінімізації логічних функцій у вигляді таблиць, які називають картами, діаграмами, таблицями. Метод таблиць Вейча застосовується для функцій, які містять не більше п’яти змінних. В цьому випадку мінімізація здійснюється для функцій записаних в ДДНФ або ДКНФ. Таблиця Вейча являє собою розкреслений прямокутник, який містить 2п клітинки, в які заносяться: · 1, якщо мінімізується функція, подана в ДДНФ; · 0, якщо мінімізується функція, подана в ДКНФ. Якщо функція подана в ДНФ (або КНФ), то її слід попередньо перетворити в ДДНФ (або ДКНФ). Спочатку виконують розмітку таблиці: змінні хі розміщують так по сторонах прямокутника, що кожна, взята окремо, змінна хі накривала 2п-1 клітинку (якщо п=3, то 23-1=4 клітинки). Для трьох змінних таблиця містить 23=8 клітинок. Разом змінні хі і
Приклади. Знайти мінімальну ДНФ функції: 1)
2)
7. Мінімізація неповністю визначених логічних функцій.
В цифрових автоматах досить часто є заборонені слова, які ніколи не надходять на вхід цього автомата. Внаслідок цього їх довільно можна позначити 0 або 1, задаючи тим самим відповідну функцію. Якщо алфавіт літер цих слів складається з 0 і 1, то маємо логічну функцію Означення. Логічна функція f, яка визначена на всіх наборах змінних, називається повністю визначеною. Означення. Логічна функція f, яка визначена не на всіх наборах змінних, називається неповністю (частково) визначеною. Нехай є неповністю визначена логічна функція f, яка невизначена p < 2n наборах змінних z1, z2,…, zn, тоді її можна доповнити 2p способами до повністю визначеної логічної функції Означення. Логічна функція Серед цих функцій Покажемо на прикладі відшукання таких функцій. Приклад. Знайти мінімальну диз’юнктивну нормальну форму логічної функції Будуємо таблицю Вейча для цієї функції. Заборонені добутки змінних, які можуть набирати значення, як 1, так і 0 (заборонені слова) залишаються порожніми клітинками, їх р=4. У цих клітинках можуть бути подані одиниці і нулі 2р=24=16 способами.

Виберемо такий розподіл одиниць і нулів, який мінімізує функцію f:
а) якщо мінімізуємо в ДНФ, то доповнюємо порожні клітинки одиницями

Результуюча функція в ДНФ матиме вигляд:
б)якщо мінімізуємо в КНФ, то доповнюємо порожні клітинки нулями і тоді результуюча функція матиме вигляд:

Контрольні запитання. 1. Яка формула алгебри висловлень називається здійсненною, нездійсненною? 2. Що називається логічним законом? 3. Сформулювати закон тотожності, суперечності, виключеного третього. 4. Яка логічна формула називається попередньою формою? 5. Що називається диз’юнктивною нормальною формою? 6. Що називається елементарним добутком? 7. Що називається конституантою одиниці? 8. Що називається досконалою диз’юнктивною нормальною формою? 9. Які перетворення треба виконати, щоб отримати ДДНФ? (*) 10. Яка ДНФ називається скороченою? Як її отримати? (*) 11. Сформулювати теорему Квайна? 12. Яка ДНФ називається тупиковою? 13. Алгоритм мінімізації логічних функцій по методу Квайна. (**) 14. Що називається конституентою нуля? 15. Яка формула називається кон’юнктивною нормальною формою? 16. Яка КНФ називається досконалою? 17. Алгоритм мінімізації логічних функцій за допомогою таблиць Вейча? (***) 18. Яка логічна функція називається неповністю визначеною? 19. Алгоритм мінімізації неповністю визначених логічних функцій? (***)
Література: О.А. Борисенко. Лекції з дискретної математики: навчальний посібник для вузів. Суми, СумДУ, 1999р. лекції 14 - 20 М.М.Швець. Азбука математичної логіки. Київ. 1965р. розділ 3
Розділ 5. Теорія графів. План. 1. Основні поняття. 2. Способи задання графів. (*) 3. Маршрути, ланцюги, цикли. 4. Ейлерів граф. 5. Дерево.(*) 6. Транспортні мережі. (**)
Часто при розв’язуванні нестандартних задач або головоломок зручно зображати об’єкти точками, а зв’язки між ними лініями або стрілками. Такий спосіб зображення ситуацій називається графом. Графи широко застосовуються в багатьох розділах прикладної математики, в програмуванні, електротехніці, в теорії планування та управління. Різноманітність застосувань графів зумовило виділення теорії графів як окремої математичної дисципліни. Теорія графів служить математичною моделлю для кожної системи, яка містить бінарне відношення. Суть методу графів полягає у представленні відношень між об’єктами у вигляді точок і відрізків, що їх з’єднують. У цьому випадку легше сприймаються і розрізняються зв’язки і відношення між об’єктами. Завдяки наочності графів можна виявляти приховані відношення, відкидати невідповідні випадки, звужуючи область повного перебору. Приклади графів: схеми автодоріг, електричне коло, план метрополітену, відрізок, квадрат, структурна формула молекули та ін.
Основні поняття. Означення. Граф – це сукупність двох множин: множини точок V і множини ліній E, між елементами яких визначено відношення інцидентності. Відношення інцидентності означає відповідність кожного елемента множини Е рівно двом елементам множини V. Елементи множини V (точки Кількість вершин графа називається його порядком: m (G).
   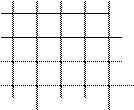
Деякі вершини графа можуть бути не сполучені ребрами. Вершини, які не належать жодному ребру називаються ізольованими. Два ребра інцидентні одній вершині називаються суміжними: Різні ребра можуть бути інцидентні одній і тій же вершині, такі ребра називаються кратними. (мал. г) Ребро, яке з’єднує вершину саму з собою називається петлею. (мал. ж) Лінії, що зображають ребра графа можуть перетинатись, але точки перетину не є вершинами. Якщо множина ребер Е порожня, то такий граф називається нуль - графом. Якщо множина V порожня, то порожньою буде і множина Е і такий граф називається порожнім. Граф, що містить кратні ребра називається мультиграфом. Граф із петлями і кратними ребрами називається псевдографом. Граф на мал. б - нескінченний. Його вершини – це точки площини з цілими координатами (х; у), а ребра, що їх з’єднують – вертикальні і горизонтальні відрізки. Якщо множини V і Е скінченні, то граф називається скінченним. Кількість ребер графа, яким належить одна вершина називається степенем вершини. Якщо всі вершини графа мають парний степінь, то граф називається парним. Граф, на кожному ребрі якого задано напрям, називається орієнтованим. Позначають D. Напрямлене ребро називається дугою.
Перша по порядку вершина називається його початком, остання – його кінцем. Орієнтований граф може містити кратні ребра, петлі, ребра, які інцидентні одній парі вершин, але мають протилежний напрям. (мал. в) Кожному неорієнтованому графу можна поставити у відповідність орієнтований граф з тією самою кількістю вершин, в якій кожне ребро замінено двома орієнтованими ребрами, інцидентними одній парі вершин і мають протилежний напрям. Таку відповідність називають канонічною. Граф, що має як ребра так і дуги називається мішаним. Два графа називаються ізоморфними, якщо у них однакова кількість вершин (по п) і вершини кожного графа можна занумерувати числами від 1 до п так, щоб вершини першого графа були сполучені ребром тоді і тільки тоді, коли відповідні вершини другого графа (тобто вершини занумеровані тими ж числами) також сполучені ребром.
2. Способи задання графів. Задати граф означає задати множини його вершин і ребер, а також відношення інцидентності. Якщо граф скінчений, то для опису його вершин і ребер їх досить занумерувати. Способи задання графів: 1) матрицею інцидентності: яка має m рядків і п стовпців. Стовпці відповідають вершинам графа, рядки відповідають ребрам графа. а) неорієнтований граф G б) орієнтований граф D
а) Якщо ребро
б) Якщо вершина
2) списком ребер: по списку ребер легко будувати матрицю інцидентності. Кожен рядок цього списку відповідає рядку матриці з тим же номером.
3) матрицею суміжності: це квадратна матриця
Для неорієнтованого графа матриця суміжності симетрична. Кількість ребер визначається верхнім правим верхнім трикутником над головною діагоналлю (10). Для орієнтованого графа суміжність визначається напрямком.
Маршрути, ланцюги, цикли. Нехай G - неорієнтований граф. Маршрутом у графі називається скінченна або нескінченна послідовність ребер ( Одне і теж ребро може зустрічатись в маршруті декілька разів. Якщо маршрут скінчений, то в ньому є початкове
Якщо ребра Нехай маршрут Кількість ребер маршруту називають його довжиною. Якщо початок і кінець маршруту співпадають, то маршрут називається циклічним. Відрізок Якщо в маршруті кожне ребро зустрічається не більше одного разу, то такий маршрут називається ланцюгом. Якщо кожна вершина графа інцидентна не більш ніж двом ребрам графа, то такий маршрут називається простим ланцюгом. Циклічний маршрут називається циклом, якщо він є ланцюгом. Маршрут, який є простим ланцюгом називається простим циклом. Цикл, який містить всі ребра графа називається обходом графа. Обхід, при якому кожне ребро графа проходиться рівно один раз називається правильним.
4. Ейлерів граф.
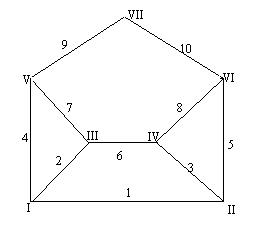
Граф, який допускає правильний обхід називається Ейлеровим. Народженням теорії графів ми зобов’язані постановці та розв’язанню задачі Леонардом Ейлером про розташування мостів у місті Кенігсберзі в часи його життя.
Задача, яку він розв’язував формулюється так:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 796; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.013 с.) |

 повинні накривати 2п клітинок (всі). Це можливо тоді, коли
повинні накривати 2п клітинок (всі). Це можливо тоді, коли  знаходяться на одному боці прямокутника. В кожній клітинці отримується логічний добуток п -змінних – конституенти одиниці. Число конституент одиниці дорівнює числу клітинок у таблиці. Важливою властивістю конституент одиниці є те, що ті з них, які стоять по краям рядків і стовпців відрізняються знаком заперечення в одній змінній. Це дозволяє здійснювати мінімізацію безпосередньо за таблицею.
знаходяться на одному боці прямокутника. В кожній клітинці отримується логічний добуток п -змінних – конституенти одиниці. Число конституент одиниці дорівнює числу клітинок у таблиці. Важливою властивістю конституент одиниці є те, що ті з них, які стоять по краям рядків і стовпців відрізняються знаком заперечення в одній змінній. Це дозволяє здійснювати мінімізацію безпосередньо за таблицею.



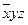



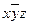





















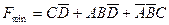
 .
. .
. на всіх наборах, на яких остання визначена, називається еквівалентною функції f (цих функцій
на всіх наборах, на яких остання визначена, називається еквівалентною функції f (цих функцій  і буде 2р).
і буде 2р). . Відомо, що функція не визначена на 4 наборах: 0110, 1011, 0011, 0010. Цим наборам відповідають конституенти одиниці:
. Відомо, що функція не визначена на 4 наборах: 0110, 1011, 0011, 0010. Цим наборам відповідають конституенти одиниці:  (заборонені слова на вході цифрового апарата), які в силу невизначеності функції f на цих чотирьох наборах можуть дорівнювати на них як 1, так і 0.
(заборонені слова на вході цифрового апарата), які в силу невизначеності функції f на цих чотирьох наборах можуть дорівнювати на них як 1, так і 0.







 1
1
 1
1


 0
0
 0
0

 ) називаються вершинами графа G; елементи множини Е (відрізки, лінії
) називаються вершинами графа G; елементи множини Е (відрізки, лінії  ) називаються ребрами графа G. Вершини та ребра називаються елементами графа.
) називаються ребрами графа G. Вершини та ребра називаються елементами графа.







 .
.





 інцидентне вершині
інцидентне вершині 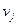 , то елемент
, то елемент  матриці дорівнює одиниці, якщо ні, то нулю.
матриці дорівнює одиниці, якщо ні, то нулю. стовпцям і рядкам якої відповідають вершини графа.
стовпцям і рядкам якої відповідають вершини графа. ) така, що кожні два сусідні ребра
) така, що кожні два сусідні ребра  мають спільну інцидентну вершину.
мають спільну інцидентну вершину. і кінцеве ребро
і кінцеве ребро 
 Вершина
Вершина  – інцидентна ребру
– інцидентна ребру  називається початком маршруту. Вершини маршруту, які не є початком і кінцем називаються внутрішніми вершинами.
називається початком маршруту. Вершини маршруту, які не є початком і кінцем називаються внутрішніми вершинами. інцидентні вершині
інцидентні вершині  ), то початок або кінець маршруту можуть одноразово виявитись внутрішньою вершиною.
), то початок або кінець маршруту можуть одноразово виявитись внутрішньою вершиною. має початок у вершині
має початок у вершині 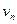 , тоді М називають маршрутом, з’єднуючим вершини
, тоді М називають маршрутом, з’єднуючим вершини  скінченого або нескінченного маршруту називається ділянкою маршруту.
скінченого або нескінченного маршруту називається ділянкою маршруту.


