
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Мінімізація логічних функційСодержание книги
Поиск на нашем сайте Мінімізація вихідної логічної функції. Термін „мінімізація” означає спрощення. Існують різні методи мінімізації логічних функцій. При мінімізації треба пам’ятати закони, правила і тотожності алгебри логіки. Скоротити логічний вираз можна використовуючи дві логічні операції: операцію склеювання і операцію поглинання. Для виконання операції склеювання виявляють у виразі функції пари членів
Дальше проводиться операція поглинання, яка основана на рівності:
Ці дві операції повторюються послідовно до тих пір, поки їх виконання виявляється можливим. Розглянемо приклад мінімізації функції, заданої в ДДНФ:
1 2 3 4 5 Попарним порівнянням членів виразу (10) (кожного з членів з усіма наступними) виявляємо пари, що склеюються: 1-ий і 2-ий; 3-ій і 4-ий; 2-ий і 5-ий (можливі й інші варіанти). В результаті склеювання одержимо:
Як видно з порівняння виразів (10) і (11), одержаний в результаті перетворення вираз значно простіший, ніж початковий. Отже, і схема побудована за виразом (11) буде значно простіша, ніж побудована за виразом (10). Мінімізація, що виконана з використанням вказаних вище процедур, вимагає певного досвіду і не може бути зведена до чітко визначених кроків. Її доцільно використовувати лише для достатньо простих логічних виразів. Мінімізація логічних функцій за допомогою карт Карно Для мінімізації більш складних виразів можна використати метод карт Карно, який дає чітко сформульовані правила виконання окремих операцій. Карта Карно представляє собою видозмінену таблицю істинності - кожна клітинка карти відповідає одному наборові аргументів. Нехай робота КЦП описується таблицею істинності (табл.6). Цій таблиці відповідає вираз (10). Табл.7 і табл..8 представляють собою карти Карно для функції трьох аргументів: в табл.2 показано відповідність клітинок карти окремим наборам, а заповнення табл.4 відповідає табл.2. При мінімізації за допомогою карти Карно об’єднуються сусідні клітинки, які містять 1. Їх можна об’єднувати по 2, по 4, по 8. В результаті об’єднання одержуємо добуток аргументів, спільних для всієї області, причому аргументи рівні нулю беруться з інверсією. Добутки, одержані для окремих областей об’єднання, додаються (виконується операція диз’юнкції).
Таблиця 6 Таблиця 7
У нашому випадку для області, яка об’єднує чотири одиниці, спільним буде аргумент Х3, який треба взяти з інверсією, а для області, яка об’єднує дві одиниці, спільними будуть - Х1 і Х2, причому Х2 треба взяти з інверсією. Таким чином одержимо вираз:
Вираз (12) представляє собою мінімальну диз’юнктивну форму логічної функції (МДФ). В карті Карно можна об’єднувати також сусідні клітинки, які містять нулі, за тими ж правилами, що і клітинки з одиницями (табл..9). В результаті об’єднання одержуємо суму аргументів, спільних для всієї області, причому аргументи рівні одиниці беруться з інверсією. Суми, одержані для окремих областей об’єднання, перемножуються (виконується операція кон’юнкції).
За табл.9 для першої області (суцільна лінія) спільними будуть аргументи Х1 і Х3, причому Х3 треба взяти з інверсією, а для другої області (пунктирна лінія) - Х2 і Х3, причому обидва аргументи треба взяти з інверсією. Таким чином, одержимо вираз:
Вираз (13) представляє собою мінімальну кон’юнктивну форму логічної функції (МКФ). Вирази, що одержані в результаті мінімізації методом карт Карно, будуть тим простішими, чим більшими будуть області об’єднання і чим цих областей буде менше.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 357; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.57.57 (0.008 с.) |

 і
і 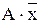 , які відрізняються лише тим, що один із аргументів в одному із членів представлений без інверсії, а в другому – з інверсією. Дальше проводиться склеювання таких пар членів, яке полягає в тому, що з цих пар виносяться за дужки спільні множники, а сума, яка залишається в дужках перетворюється на 1:
, які відрізняються лише тим, що один із аргументів в одному із членів представлений без інверсії, а в другому – з інверсією. Дальше проводиться склеювання таких пар членів, яке полягає в тому, що з цих пар виносяться за дужки спільні множники, а сума, яка залишається в дужках перетворюється на 1: . (8)
. (8) (9)
(9) (10)
(10)
 (11)
(11) х2х1
х2х1
 х2х1
х2х1
 , (12)
, (12) х2х1
х2х1
 (13)
(13)


