
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Представлення функцій f4 в канонічній формі алгебри Пірса.Содержание книги
Поиск на нашем сайте
В даній алгебрі визначені функції {АБО-НЕ}.
В даній алгебрі визначені функції {І-НЕ}.
Визначення належності функції f4 до п’яти чудових класів 1. Дана функція зберігає нуль, так як F(0000)=0. 2. Дана функція зберігає одиницю, так як F(1111)=1. 3. Дана функція не самодвоїсна, так як F(1001)=1, F(0110)=0. 4. Дана функція не монотонна, так як F(0001)> F(0010). 5. Дана форма нелінійна, так як канонічна форма алгебри Жегалкіна, що отримана у підрозділі 3.3 є не лінійним поліномом. На основі вищесказаного робимо висновок, що функція f4 належить першим двом і не належить останнім трьом передповним класам. Мінімізація функції f4 методом невизначених коефіцієнтів Ідея цього методу полягає у відшуканні ненульових коефіцієнтів при кожній імпліканті. Рівняння для знаходження коефіцієнтів представимо таблицею (таблиця 3.7.1). Виконаємо викреслення тих рядків на яких функція приймає нульові значення. Викреслимо вже знайдені нульові коефіцієнти в тих рядках таблиці, що залишилися імпліканти, що залишилися після виконання попередніх дій поглинають ті імпліканти, що розташовані зправа від них.
Таблиця 3.7.1 – таблиця невизначених коефіцієнтів

Отримаємо СДНФ функції, яка і буде МДНФ:
Мінімізація функції f4 методом Квайна-Мак-Класкі Виходячи з таблиці істинності функції, запишемо стовпчик ДДНФ, розподіливши терми за кількістю одиниць. Проводимо попарне склеювання між сусідніми групами. Подальше склеювання неможливе. Виконаємо поглинання термів(рисунок 3.8.1).
Рисунок 3.8.1 – Поглинання термів
Як можна побачити, ми одержали тіж самі імпліканти, що і при мінімізації методом невизначених коефіцієнтів. Тому результат буде той самий:
Мінімізація функції f4 методом діаграм Вейча
Рисунок 3.9.1 - мінімізація функції методом Вейча
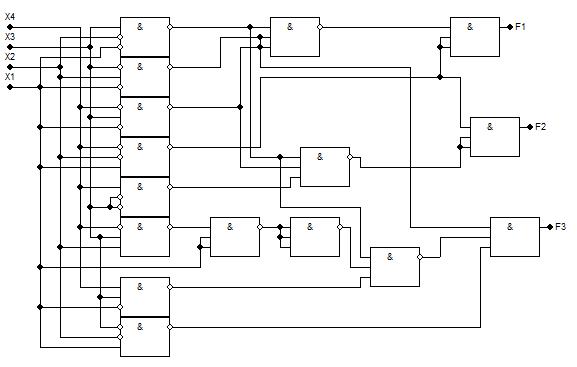
Спільна мінімізація функцій f1, f2, f3 Щоб одержати схеми з мінімальними параметрами необхідно виконати сумісну мінімізацію системи функцій та їх заперечень. Виконаємо мінімізацію системи функцій f1, f2, f3, заданих таблицею істинності (технічного завдання КПІ.109109.002 ТЗ) методом Квайна-Макласкі. Особливості мінімізації системи перемикальних функцій порівняно з мінімізацією однієї функції: 1. Під час запису конституент усі невизначені набори рахуемо за 1. 2. Невизначені набори не записуються до таблиці покриття 3. Склеювання можливе лише якщо у імплікант співпадає хоча б одна покрита функція. Нова імпліканта покриває множину функцій, що є перетином множин вхідних імплікант. 4. Поглинання можливе лише якщо співпадають усі покриті функції.
Таблиця 3.10.1 – Таблиця покриття ДДНФ
Виведемо нормальні формі:
Виконаемо мінімізацію ДДНФ заперечення: Склеювання і поглинання імплікант:
Таблиця 3.10.2 – Таблиця покриття ДДНФ заперечення
Виведемо нормальні формі:
Рисунок 3.10.1 - Схема І-НЕ/І-НЕ. Складність за Квайном К=57. Затримка t=4tІ-НЕ
Рисунок 3.10.2 - Схема І-НЕ/І. Складність за Квайном К=48. Затримка t=4tІ-НЕ +4tІ
Одержання операторних форм для реалізації на ПЛМ Одержимо операторне представлення функцій на ПЛМ. На ПЛМ можна реалізувати форми {І/АБО, І/АБО-НЕ}.
І/АБО: Всього 4 змінні, 9 імплікант, 3 функції. Тож оберемо ПЛМ(4,9,3). Побудуємо карту програмування ПЛМ (рисунок 3.12.1).
Рисунок 3.12.1 - мнемонічна схема ПЛМ Покажемо умовне графічне позначення даної ПЛМ (рисунок 3.12.2)
Рисунок 3.12.2 - умовне графічне позначенняПЛМ Висновок
Метою даної курсової роботи було закріпити навички абстрактного та структурного синтезу автомата по заданому алгоритму роботи. Постало питання мінімізації систем функцій для зменшення кількості логічних елементів та збільшення швидкодії схеми. При побудові комбінаційних схем було показано доцільність та ефективність сумісної мінімізації кількох функцій. Усі схеми та керуючий автомат були перевірені в програмі AFDK 2.0. Перевірка дала позитивні результати. Також я покращив навички оформлення текстову конструкторську документацію відповідно до діючих стандартів.
1) Жабін В.І.,Ткаченко В.В. Логические основы и схемотехника цифровых ЭВМ.–Київ ТОО "Век+",1999. 2) Самофалов К.Г., Корнійчук В.І., Тарасенко В.П. Электронные цифровые вычислительные машины. – К. Вища школа, 1983. 3) Савельєв А.Я. Арифметические и логические основы цифровых автоматов.– Москва: Энергия,1974 г. 4) Поспелов Д.А. Логические методы анализа и синтеза схем.– Москва: Энергия,1974г. 5) Хоуп Г. «Проектирование цифровых вычислительных машин и интегральных схем.» Москва: Мир, 1984 г.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 233; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.85.96 (0.009 с.) |

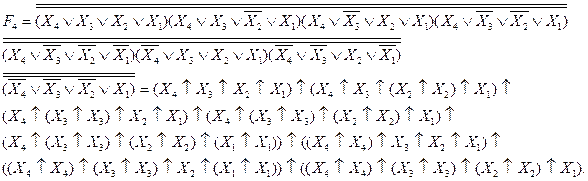

 3.5 Представлення функцій f4 в канонічній формі алгебри Шеффера
3.5 Представлення функцій f4 в канонічній формі алгебри Шеффера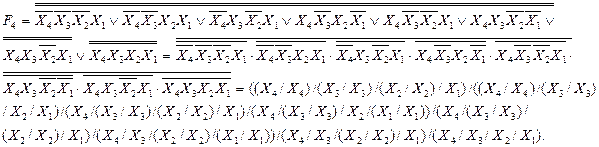

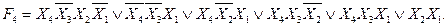
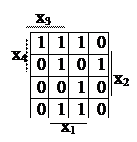 Виконаємо мінімізацію функції методом Вейча (рисунок 3.9.1). Цей метод дуже зручний при мінімізації функції з кількістю аргументів до чотирьох включно. Кожна клітинка відповідає конституенті, а прямокутник з кількох клітинок – імпліканті.
Виконаємо мінімізацію функції методом Вейча (рисунок 3.9.1). Цей метод дуже зручний при мінімізації функції з кількістю аргументів до чотирьох включно. Кожна клітинка відповідає конституенті, а прямокутник з кількох клітинок – імпліканті.

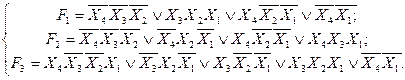 І/АБО
І/АБО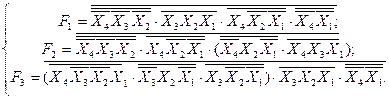 І-НЕ/І-НЕ
І-НЕ/І-НЕ
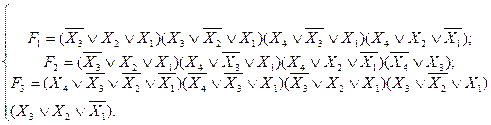 АБО/І
АБО/І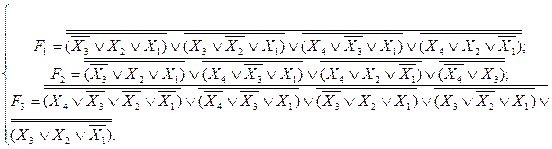 АБО-НЕ/АБО-НЕ
АБО-НЕ/АБО-НЕ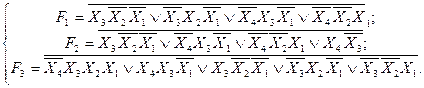 І/АБО-НЕ
І/АБО-НЕ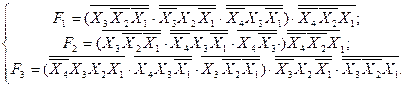 І-НЕ/І
І-НЕ/І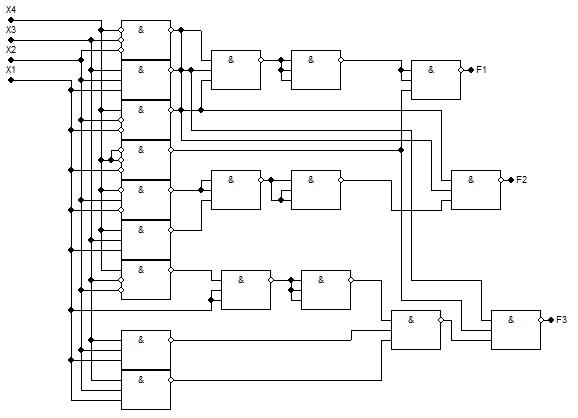


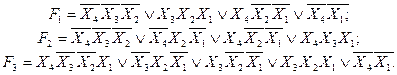









 X4
X4



 X3
X3




 X2
X2



 X1
X1

 F1
F1



 F2
F2


 F3
F3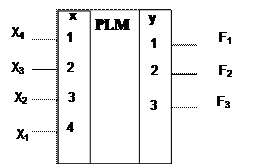

 5 Список літератури
5 Список літератури


