
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Мінімізація логічних функцій методом Квайна.Содержание книги
Поиск на нашем сайте
Метод мінімізації логічних функцій базується на теоремі Квайна: якщо в ДДНФ логічної функції F виконати всі операції неповного склеювання, потім усі операції поглинання, то буде одержана скорочена ДНФ цієї функції, тобто диз’юкція всіх її простих імплікант. Особливістю метода мінімізації за Квайном є те, що його робота починається після подання в ДДНФ логічної функції, що мінімізується. Тому, якщо функція задана в довільній ДНФ, то її спочатку слід перетворити в ДДНФ шляхом її розгортання. Потім необхідно виконати слідуючи кроки: 1) у ДДНФ функції F=F(x1, x2, …, xn) здійснюються всі операції неповного склеювання конституент одиниці. Неповне склеювання викликано тим, що кожна конституента одиниці водночас може склеюватися з кількома іншими. У результаті одержують імпліканти, що мають по (n-1) змінних. При цьому можливе також отримання і простих імплікант. 2) Відбувається поглинання імплікантами всіх конституент одиниці, які беруть участь у неповному склеюванні. Конституенти одиниці, що беруть участь в операціях неповного склеювання, обов’язково поглинаються, бо вони містять у своєму складі імпліканти, які мають після першого склеювання по (п-1) літер і містяться у функції F. Конституенти одиниці, які не були задіяні в операціях склеювання, не можуть поглинатися, бо вони є простими імплікантами з п змінними. 3) Здійснюються операції неповного склеювання і поглинання імплікант з (п-1) змінною, одержаних на першому кроці склеювання. Ця процедура повторюється доти, поки операції неповного склеювання залишаються можливими. Отримана в результаті ДНФ буде скороченою. Результати склеювання записують в таблицю:
Якщо серед простих імплікант, що містяться в скороченій ДНФ функції, є такі, що входять до початкової функції F, то решта простих імплікант вважаються зайвими. Означення. Диз’юнкція простих імплікант, жодна з яких не є зайвою, називається тупиковою ДНФ логічної функції. Тупикових функцій може бути декілька. Тоді виникає завдання пошуку такої тупикової логічної функції, яка б мала мінімальну кількість літер. Така функція називається мінімальною ДНФ. Деякі логічні функції можуть мати кілька мінімальних ДНФ, що містять однакову кількість літер. У цьому випадку вибирається мінімальна ДНФ, яка більш придатна для технічної реалізації в цифровому пристрої або програмі. Імплікантні матриці. З метою визначення мінімальної ДНФ використовуються імплікантні матриці
Це таблиця, по горизонтальних входах якої записуються прості імпліканти цієї функції, одержані зі скороченої ДНФ; по вертикальних входах записуються конституенти одиниці, які входять в задану функцію. Якщо імпліканта є власною частиною деякої конституенти одиниці, то клітинка імплікантної матриці, що відповідає цій імпліканті і конституенті одиниці, відмічається хрестиком. Щоб одержати мінімальну ДНФ заданої функції, треба знайти мінімальну кількість імплікант, які разом накриють хрестиками всі стовпці імплікантної матриці.
Приклад. Знайти мінімальну ДНФ логічної функції F=F(x1, x2, x3, x4), яка дорівнює одиниці на наборах з номерами 1, 3, 5, 7, 14, 15 і дорівнює нулю на решті наборів. Подамо функцію в ДДНФ:
1) виконаємо всі можливі неповні склеювання першого члена, потім другого, третього і т. д. Проведемо всі можливі операції поглинання конституент одиниці і результат запишемо у таблицю (перше склеювання)
З таблиці видно, що всі конституенти одиниці поглинаються імплікантами, отриманими після склеювання. В результаті отримуємо таку функцію:
2) проведемо друге склеювання конституент одиниці:
До цього виразу операції неповного склеювання і поглинання виконати не можна, і тому він є скороченою ДНФ заданої логічної функції.
3) будуємо імплікантну матрицю для одержаної функції F.
З таблиці випливає, що до мінімальної форми має обов’язково увійти імпліканта
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 736; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.224.30 (0.008 с.) |










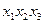









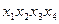
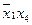
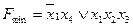 .
.


