Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розділ 2. Вектори, відношення, відображення.
План. 1. Вектори і прямий добуток множин. 2. Відношення. (*) 3. Відображення. (*) 4. Функції. 5. Перетворення. (*) 6. Сукупність підстановок множини М. (**) 7. Алгебраїчні операції та системи. (***) Вектори і прямий добуток множин.
Математика вивчає властивості певних множин елементів, відношень між ними. Найбільш поширеними і важливими для математики є відношення між парами і трійками елементів. Якщо елементи скінченної множини як-небудь перенумеровані, то кажуть, що дана множина упорядкована. Одну і ту ж множину можна упорядкувати різними способами. Наприклад: множину учнів у класі можна впорядкувати - по алфавіту; - по росту; - по вазі і т. д. Нехай дані множини Х1, Х2, …Хn. Кортежем (вектором) довжини п складеним з елементів цих множин називається скінченна послідовність α = (х1, х2, …хn), де хі є Хі; хі називається координатою кортежу α. Кортеж – це упорядкований набір елементів. Координати нумерують зліва направо. Довжиною кортежу називається кількість його координат. Кортеж позначають (А,В), де на першому місці елемент множини А, на другому місці елемент множини В. Приклад: А={а,b,с}, В={1,2} α ={(а;1),(а;2),(b;1),(b;2),(с;1),(с;2)} Будь-яке слово є кортеж складений з літер. Будь-яке натуральне число – це кортеж складений з цифр. Кортежі довжини 2 (2 елементи) називаються парами; довжини 3 –трійками; довжини n – енками. Два кортежі рівні, якщо вони мають однакову довжину і їх відповідні координати рівні: Приклади: а) (1; 2; 3)=( б) (1;2;3)≠(3;1;2) Порожній кортеж – це кортеж, що не має жодної координати, його довжина дорівнює нулю. Чим відрізняється кортеж від множини: 1) у множині порядок елементів може бути різний, а кортежі різні якщо не співпадає порядок; {а; b;с}={ b;а;с} (а; b;с)≠(а;с; b) 2) у множині всі елементи різні, а у кортежі вони можуть повторюватись: {а; b;с}, (а;b;с;b) Приклади: 1) слово «підручник» – це кортеж довжини 9: (п;і;д;р;у;ч;н;и;к) 2)число 134 – це кортеж довжини 3: (1;3;4) Утворення впорядкованих m -ок (кортежів довжини m) пов’язане з операцією над множинами, яку називають знаходженням прямого або декартового добутку множин. Розглянемо випадок, коли m=2. Прямим (декартовим) добутком двох множин А і В називається множина всіх пар (а; b) таких, що а є А, b є В: А × В ={(а; b)│ а є А, b є В}
А×В = Ø, якщо А = Ø, або В = Ø, або А =В = Ø Прямим добутком множин Прямий добуток А×А позначають А2 і називають прямим квадратом множини А. Зауваження: А×В ≠ В×А. Прямим добутком трьох множин А, В, С називається множина всіх кортежів (а, b, с) таких, що а є А, b є В, с є С. А× В ×С = {(а, b, с)| а є А, b є В, с є С}. А × А × А =А3 –прямий куб множини А. Якщо множини А, В, С мають потужність m, n, k, то потужність множини А×В×С дорівнює добутку потужностей цих множин. |А| =m, |В| =n, |С| = k, то |А ×В× С|= m · n · k. Якщо R - множина дійсних чисел,то R2 =R×R. Геометричною ілюстрацією прямого квадрата є множина точок прямокутної системи координат на площині (х;у) R×R×R=R3, геометрична ілюстрація – це множина точок тривимірного простору.
Відношення. Поняття “відношення” поширене як в математиці так і за її межами. Так, наприклад, говорять про родинні відносини між певними людьми, про відносини між людьми на роботі. В математиці говорять про відношення подільності чисел, паралельності та перпендикулярності прямих на площині, подібності фігур і т.д. Основну ідею поняття “відношення” можна розглянути на таких прикладах: А={3;5;8}, В={1;4;11} Побудуємо множини правильних висловлень: М1={“3:1”, ”5:1”, ”8:1”, ”8:4”} М2={“3>1”, ”5>1”, ”8>1”, ”5>4”, ”8>4”} Кожний елемент з множини М1 є висловлення про відношення подільності, а кожний елемент з множини М2 є висловлення про відношення “більше”. Кожне з висловлень множини М1 можна замінити відповідною парою (а; b), в якій а Відношення “більше” в множинах А і В можна зобразити відповідною множиною
Бінарним відношенням, визначеним у множинах А і В називається кожна підмножина прямого добутку множин А і В.
Позначають: α, β, γ,…Ρ, Μ, Ν… Якщо А=В, то кажуть, що бінарне відношення визначене у множині А. Відношення полягають у тому, що деяким елементам множини А поставлені у відповідність елементи множини В. Множина А називається множиною відправлення (визначення), а множина В - множиною прибуття (значень). Під об’ємом відношення α розуміють склад тих пар, які входять в α. Якщо елементи а і b пари (а;в) перебувають у відношенні α, то позначають так: (а;в) В утворенні пар бінарного відношення можуть брати участь не всі елементи множин А і В. Способи задання відношень. 1) переліком всіх своїх елементів; 2) характеристичною властивістю: 3) графічно (множиною точок на площині): А={1;2;3;4;5}, В={а; b;с;d}
4)
5)табличний:
Множина всіх b прообразом b в А. Відношенням оберненим до Р (Р Позначають: Р-1, α –1: (b;а) Приклад: А={3;4;6;7}, В={2;3;4}. Задати Р-1, де Р –відношення подільності. Р={(3;3), (4;4), (4;2), (6;2), (6;3)}, Р-1= {(3;3), (4;4), (2;4), (2;6), (3;6)} З означення випливає, що обернене до відношення Р-1 буде відношення Р: (Р -1)-1 = Р Щоб дістати стрілкове відношення Р-1, треба стрілки відношення Р поміняти на протилежні. Композицією відношень називається послідовне застосування двох відношень. Композиція відношень - це операція з трьома множинами Χ, Υ, Ζ на яких визначені дві відповідності Р і Q: (Х;Y;Р) і (Y;Z;Q), де Р Композицію позначають Р ο Q, при цьому композицію відношень записують: (X, Z, P ο Q), P ο Q Властивості відношень. 1) рефлексивність: Якщо властивість рефлексивності не виконується, то відношення називається антирефлексивним: 2) симетричність: Якщо властивість симетричності не виконується, то відношення називається антисиметричним: Асиметричне відношення: 3) транзитивність: Якщо властивість транзитивності не виконується, то відношення називається антитранзитивним: 4) властивість повноти: Відношення називається еквівалентним, якщо одноразово виконуються властивості рефлексивності, симетричності і транзитивності. Еквівалентність розбиває множину на підмножини. Відношення строгого порядку, якщо воно асиметричне і транзитивне одночасно. Відношення нестрогого порядку, якщо воно асиметричне, транзитивне і рефлексивне.
3. Відображення. 4. Відображенням множини А в множину В називається відношення, в якому кожному елементу множини А ставиться у відповідність не більш ніж один, однозначно визначений елемент множини В.
Елемент b множини В називається образом елемента a множини А, в свою чергу елемент a називається прообразом елемента b. Відображення однієї множини в іншу позначається малими літерами грецького алфавіту φ, α, β … φ: А→В або А→В. Образ елемента a позначається: (a)φ. Способи відображення однієї множини в іншу: 1) графічний; 2) стрілковий; 3) табличний. Приклад 1. А={2;3;6;7}, В={4;9;11;12;28} φ: А→В –це відображення, яке кожному числу з множини А ставить у відповідність найменше спільне кратне цього числа і числа 4, яке входить до множини В. (3) φ = 12 12- образ 3, 3- прообраз 12 (6) φ =12 12- образ 6, 6- прообраз 12. (2) φ = 4 4 - образ 2, 2- прообраз 4. Стрілкова схема:
Табличний спосіб задання:
Приклад 2. А={г;а;и;л}, В={1;2;3;4;5;6;7} φ: А→В –це відображення, за яким кожній літері з множини А ставиться у відповідність її порядковий номер у слові “ логарифм”.
А
Стрілкове задання: А={г;а;и;л}
В={1;2;3;4;5;6;7} Види відображень: Сюр’єкція – це відображення множини А в множину В, при якому для кожного елемента b з множини В знайдеться елемент a з множини А такий, що (a)φ = b. А={2;3;6;7}, В={4;12;28}
В={4; 12; 28} Табличне задання:
Якщо множини А і В скінченні, то в нижньому ряду таблиці знаходяться всі елементи множини В, хоча можливо і не один раз. В стрілковому зображенні в кожний елемент множини В входить хоча б одна стрілка. Сюр’єкція скінченної множини на скінченну множину існує не завжди. Щоб відображення φ: А→В було сюр’єкцією необхідно, щоб виконувалась умова │А│≥│В│. Ін’єкція. Відображення множини A на множину B називається ін’єкцією, якщо різним елементам множини А відповідають різні елементи множини В: a1≠a2 В нижньому ряду таблиці ін’єктивного відображення кожний елемент множини В присутній один раз. При стрілковому зображенні ін’єкції в кожний елемент множини В, входить не більше ніж одна стрілка. Ін’єкція можлива, якщо │А│≤│В│.
В={10;15;20;25;30;35;40;45}
Бієкція. Якщо відображення множини А на множину В є одноразово сюрєктивним та інєктивним, то воно називається взаємно-однозначним або бієкцією множини А на множину В.
Бієкція можлива, якщо виконується рівність │А│=│В│. Схематично бієктивне відображення позначається так: А
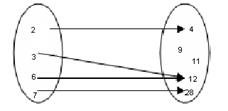
Функції. Функцією Елемент Функції Якщо область визначення функції складається з одного елемента, то функція називається функцією-константою. Символ 1) 2) Формальне означення функції: Способи задання функції: 1) перерахуванням всіх пар
2) у вигляді формули, що містить перелік математичних операцій, які мають бути виконані над Якщо Вираз, що містить функціональні знаки і символи аргументів називають формулою. Якщо у виразі Якщо Функція типу Композиція функцій
Більш загальним поняттям, ніж функція є поняття функціоналу. Функціонал встановлює залежність між деякою множиною чисел і деякою множиною функцій (залежність числа від функції). Наприклад: означений інтеграл Оператор – це більш загальне поняття. Він встановлює залежність між двома множинами функцій так, що кожній функції з однієї множини відповідає певна функція з другої множини. Приклад: Р – оператор диференціювання, тоді зв’язок між похідною:
Перетворення. Перетворення – це відображення множини Табличний вигляд перетворення має вигляд Приклад. Нехай задана множина Для множини М можуть бути такі перетворення а) Деякі перетворення множини М мають спеціальну назву. 1) Тотожне перетворення – це перетворення множини М, при якому всі елементи з М залишаються на місці 2) Постійне перетворення – це перетворення, при якому кожному елементу з множини М ставиться у відповідність деякий фіксований елемент цієї множини: 3) Підстановка – це бієкція множини М на себе. Композицією перетворень φ і ψ називається таке перетворення ω, який кожний елемент Приклад. Нехай φ: х→х+3 – перетворення множини дійсних чисел R, яке числу х ставить у відповідність число х+3, а ψ: х → х+2, тоді перетворення ώ є композиція
φ: х → х+3 ψ: х → х+2 ω: φ ◦ ψ: x → x+5 Якщо х=3, то φ ◦ ψ: 3 → 8 6. Сукупність підстановок множини М: S(М). Розглянемо множину
Підстановки Цю властивість: переводити елементи з області визначення в одні і ті ж елементи, використовують при послідовному виконанні перетворень, яке називається композицією або добутком підстановок. 1) Покажемо, що добуток підстановок належить сукупності підстановок
Отже, якщо 2) Перевіримо чи виконується асоціативний закон для множення підстановок
а)
б)
3) Перевіримо що буде, якщо
Висновок: 4) Знайдемо добуток:
Отже
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1071; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.139.59 (0.132 с.) |
 , якщо
, якщо 
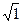 ;
; 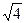 ;
; 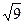 )
)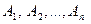 називається множина всіх кортежів довжини n виду
називається множина всіх кортежів довжини n виду 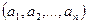 , таких, що
, таких, що 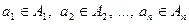 .
.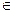 А, b
А, b 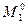 таких пар:
таких пар: 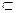 (А×В). Отже, замість множини
(А×В). Отже, замість множини 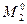 пар (а;b), в яких перша компонента а
пар (а;b), в яких перша компонента а 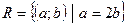






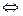 (а; b)
(а; b) 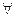 а
а 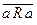 .
.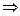 в R а
в R а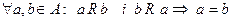
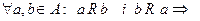 Æ
Æ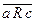 .
.


 Графічне задання: В
Графічне задання: В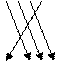
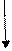

 Стрілкове задання: а) А={2; 3; 6; 7}
Стрілкове задання: а) А={2; 3; 6; 7}
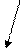


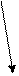
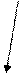
 А={1;2;3;4}
А={1;2;3;4}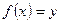 називається відображення, що ставить у відповідність кожному елементу
називається відображення, що ставить у відповідність кожному елементу  з області визначення
з області визначення 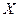 єдиний елемент
єдиний елемент  з області значень
з області значень  .
.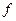 і
і  називаються рівними, якщо їх область визначення є одна і та сама множина
називаються рівними, якщо їх область визначення є одна і та сама множина 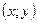 , які беруть участь у відношенні між множинами
, які беруть участь у відношенні між множинами 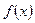 - це означення для
- це означення для  , що відповідає
, що відповідає 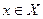 .
. .
.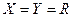 і
і 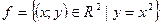 , то
, то 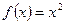 .
. ,
,  , то будемо мати функцію від двох змінних
, то будемо мати функцію від двох змінних 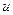 і
і 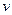 , яка позначається
, яка позначається 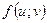 , де
, де 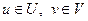
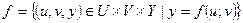
 , то оберненими до них є функції
, то оберненими до них є функції 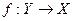 ,
, 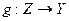
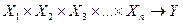 називається n -місною. Така функція має n аргументів і позначається
називається n -місною. Така функція має n аргументів і позначається 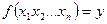 , де
, де 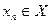 ,
,  , для кожного
, для кожного 

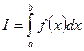 ,
,  - функціонал – це число, що залежить від функції
- функціонал – це число, що залежить від функції 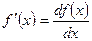 і функцією
і функцією 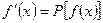 .
. самої на себе.
самої на себе.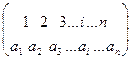 де
де 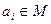 .
.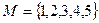
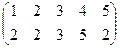 б)
б) 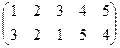 в)
в) 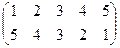 та інші.
та інші. .
.
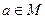 .
.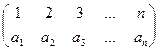 , де
, де  ,
, 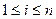
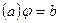 , а потім в
, а потім в 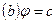 :
: 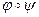 :
: 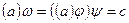
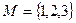 . Підстановками на множині М будуть
. Підстановками на множині М будуть
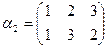
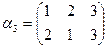
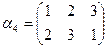
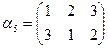

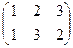 і
і  - рівні, бо в них область визначення (елементи 1,2,3) одна і та ж, і кожний елемент з області визначення ці підстановки переводить в одні і ті ж елементи: 1→1, 2→3, 3→2.
- рівні, бо в них область визначення (елементи 1,2,3) одна і та ж, і кожний елемент з області визначення ці підстановки переводить в одні і ті ж елементи: 1→1, 2→3, 3→2.
 і
і  , то
, то 
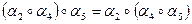 ?
?




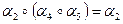 Отже, асоціативний закон виконується.
Отже, асоціативний закон виконується.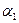 множити на будь-яку підстановку з множини М.
множити на будь-яку підстановку з множини М.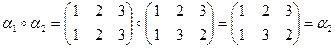
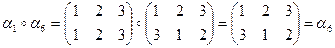
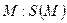 .
.