
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні закони алгебри логіки.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В алгебрі логіки існують логічні закони, логічні суперечності, або твердження, що логічно виконуються. * Логічним законом називається складне висловлення, яке є істинним при всіх можливих комбінаціях значень, висловлень які до нього входять.
* Логічною суперечністю називається складне висловлення яке є завжди хибним, при всіх можливих комбінаціях значень, висловлень, які до нього входять.
* Твердженням, що логічно виконується називається складне висловлення, яке є істинним для одних значень простих висловлень і хибним для інших значень простих висловлень.
Основні закони алгебри логіки:
4. Логічна функція. * Логічною називаєтьсяфункція F від n змінних, х1...хn, яка так само, як і аргументи може набирати лише два значення 0 і 1. х1; х2;... хn – аргументи функції.
· Набором називається сукупність а1;а2;...аn значень змінних х1; х2;.... хn.
Теорема: Кількість наборів для аргументів х1; х2;.... хn логічної функції N=2n
Набори для аргументів х1; х2 .
Теорема: Кількість різних логічних функцій від n аргументів Якщо n=1 (одна змінна), то N=2; M=22=4 Якщо n=2 (дві змінних), то N=22=4; М=24=16
Таблиці істинності: для одного аргументу існують 4 різні логічні функції
для двох змінних А і В існує N=22=4 набори і М=16 логічних функцій.
1) F=0 5) F=А 2) F=1 6) F=A│B 10) F=A 3) F=A 7) F=A 4) F=B 8) F=A Розглянуті 16 логічних функцій для двох змінних носять назву елементарних. Це ті функції, на основі яких будується алгебра логіки і її застосування в науці і техніці. Серед цих 16 функцій є базисні, за допомогою яких одержують інші функції.
Базисні: 1/ F=1 2/ F=0 3/ F=A 4/ F=A→B (інверсія) 5/ F= 6/ F=
Для елементарних функцій існує ряд важливих формул, які перевіряються в таблицях істинності: 1) Правило Де Моргана:
2) Правило Де Моргана: 3) A 4) A ~ B= У разі коли одним з аргументів є F=1, або F=0, то справедливі слідуючи співвідношення:
Співвідношення для аргументів Х1 і Х2:
Бульові функції. Якщо взяти будь-яку формулу алгебри висловлень, то її значення істинності буде функцією значень істинності простих висловлень з яких вона складається. Ця функція має властивість: вона сама і її аргументи набувають лише двох значень 0 і 1. Такі функції називаються двозначними або бульовими функціями. Назва дана в честь англійського математика дев’ятнадцятого століття Джорджа Буля, що заклав основи бульової алгебри. Область значень бульової функції і її аргументів складається з двох елементів: істинності і хибності, а область існування (визначення) – з n- місних наборів.
Приклади бульових функцій в науці і практиці: - це фізичні системи, які діють за принципом „так – ні ”. Простими елементами таких систем є вимикачі, перемикачі, електричні і електронні лампи, кожен з яких може бути в двох стійких положеннях або станах. В таких же станах може бути і вся система залежно від стану її елементів.
Отже значення бульової функції і її аргументів найрізноманітніші: - істинність – хибність; - так – ні; - струм проходить – не проходить; - лампа горить – не горить і т. д. Аргументи бульової функції називаються бульовими змінними. Різниця між бульовими функціями і алгеброю висловлень: - алгебра висловлень розглядає тільки функції істинності висловлень, тобто обме жена чисто логічним матеріалом; - теорія бульових функцій відкидає обмеженість і виходить на широкий простір будь-яких двозначних зв’язків між будь-якими предметами (об’єктами);
- закони теорії бульових функцій мають більш загальний характер і знаходять більше застосувань в науці і практиці; - теорія бульових функцій вийшла за межі чистої логіки. Алгебра висловлень – це лише одна з галузей теорії бульових функцій. Теорія бульових функцій застосовується в: - релейно-контактних схемах; - дискретних автоматах; - електронно-цифрових обчислювальних машинах; - деяких питаннях математики. Бульова алгебра – це множина бульових функцій, які розглядаються разом з трьома основними операціями: - кон’юнкцією; - диз’юнкцією; - запереченням. Ці операції називаються бульовими, а формули бульової алгебри – бульовими формулами.
Основні формули бульової алгебри:
Спеціальні формули бульової алгебри:
Контрольні запитання. 1. Що таке математична логіка? 2. Що називається висловленням? Наведіть приклади. 3. Яке висловлення називається простим, складним? Наведіть приклади 4. Сформулювати означення основних логічних операцій, їх таблиці істинності.(*) 5. Що називається логічним законом? 6. Що називається логічною суперечністю? 7. Що називається твердженням, що логічно виконується? 8. Назвати та записати основні закони алгебри логіки. (**) 9. Яка функція називається логічною? 10. Які функції є базисними? 11. Яка функція називається бульовою? 12. Де застосовується теорія бульових функцій? 13. Записати основні формули бульової алгебри.(*)
Література: О.А. Борисенко. Лекції з дискретної математики: навчальний посібник для вузів. Суми, СумДУ, 1999р. лекції 11 - 13 Ю.В. Нікольський, В.В.Пасічник, Ю.М. Щербина. Дискретна математика. Підручник для вищих навчальних закладів. Київ. 2007р. розділ 1. п. 1.1 – 1.8 М.М.Швець. Азбука математичної логіки. Київ. 1965р. розділ 1,
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 770; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.180.166 (0.011 с.) |

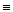 А
А
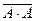 =1
=1
 +
+  = 1
= 1
 =1; А+А=А.
А+В=В+А;
=1; А+А=А.
А+В=В+А;
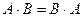 (АВ)С=А(ВС)
А+(В+С)=(А+В)+С
(А+В)·С= АС+ВС
А(А+В)=А
А+АВ=А
(АВ)С=А(ВС)
А+(В+С)=(А+В)+С
(А+В)·С= АС+ВС
А(А+В)=А
А+АВ=А
 =
= 
 =
= 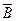
 А·1=А
А+1=1
А·1=А
А+1=1
 А+0=А
А+0=А

 B 9) F=A
B 9) F=A  B 13) F=A~B
B 13) F=A~B B 14) F=A
B 14) F=A  B
B B 11) F=B
B 11) F=B  B 12) F=B
B 12) F=B 
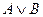
 =
= 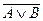
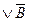 =
= 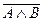
 (
( )(
)( )
)





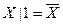



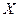
















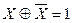


















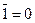




 (закон контрапозиції).
(закон контрапозиції).


