
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава II. Алгебры. Алгебраические системы.Содержание книги
Поиск на нашем сайте
Глава II. Алгебры. Алгебраические системы. 1. Операции на множествах. Под операциями на множестве М понимают правило или закон, по которому выполняются некоторые действия над элементами множества М. Пример. Операции Под бинарной операцией на множестве М понимают правило или закон, по которому выполняется некоторое действие над двумя элементами множества М; под унарной операцией на множестве М понимают правило или закон, по которому выполняется некоторое действие над одним элементом из М. Пример. В общем случае результат выполнения операции на множестве М не обязан принадлежать множеству М. Пример. На множестве ℕ: 3-5 В общем случае результат выполнения операции не обязан определяться однозначно. Пример. « ∘» на ℕ a ∘ b = a Операции на множествах, для которых результат определяется однозначно и принадлежит исходному множеству, называются алгебраическими. Определение 1. Бинарной алгебраической операцией на множестве М называется отображение Вместо Пример. «+»: а + b = с. Определение 2. Непустое множество М с определенными на нем алгебраическими операциями и отношениями называется алгебраической системой.
Тогда полученную алгебраическую систему обозначают < M, Пример. <ℤ, {+, ⋅}, { Определение 3. Непустое множество с определенными на нем алгебраическими операциями называется алгеброй. Из определений 2 и 3 Пример. < Z, {+,⋅}> - алгебра. Определение 4. Алгебра < М, ∘ > называется группоидом, если ∘- бинарная алгебраическая операция. Определение 4’. Непустое множество с определенной на нем бинарной алгебраической операцией называется группоидом.
Группы. Определение 13. Непустое множество G с определённой на нём бинарной алгебраической операцией ∘ называется группой, если выполняются следующие аксиомы (аксиомы группы): 1) Операция ∘ ассоциативна на G,т. е. а ∘(b ∘ c) = (a ∘ b)∘ c, "a, b, c Î G. 2) В G существует нейтральный элемент относительно операции ∘ т. е. $ e Î G: " a Î G: a ∘ e = e ∘ a = a. 3) Для каждого элемента из G в G существует симметричный ему элемент, относительно операции ∘, т. е. " a Î G $ a' Î G: a∘ a' = a' ∘ a = e. Примеры. <ℕ, +> - не является группой, так как не выполняется аксиома 2) (0 Ï ℕ), но является полугруппой с сокращением; <ℕ, ‧> - не является группой, так как не выполняется аксиома 3) (5 Î ℕ, но 1/5 ∉ ℕ), но является моноидом и полугруппой с сокращением; <ℤ, +> - группа; <ℤ, ‧> - не является группой, так как не выполняется аксиома 3) (5 Î ℤ, но 1/5 ∉ ℤ), но является моноидом и полугруппой с сокращением (для ℤ#); <ℚ, +>, <ℝ, +> - группы; <ℚ, ‧>, <ℝ, ‧> - не являются группами, так как не выполняется аксиома 3) (для нуля нет обратного); <ℚ#, ‧>, <ℝ#, ‧> - группы. Определение 14. Группа G относительно операции ∘ называется абелевой, если операция ∘ коммутативна на G, т. е. a ∘ b = b ∘ a, " a, b Î G. Определение 15. Группа относительно сложения называется аддитивной. Нейтральный элемент е в ней называется нулевым и обозначается 0. Симметричный элементу а элемент а ’ называется противоположным и обозначается – а. Определение 16. Группа относительно умножения называется мультипликативной. Нейтральный элемент е в ней называется единичным и обозначается 1. Симметричный элементу а элемент а ’ называется обратным и обозначается а -1. Пример. ℤ, ℚ, ℝ – аддитивные группы; ℝ#, ℚ# - мультипликативные группы. Определение 17. Группа G называется конечной, если она содержит конечное число элементов. В противном случае группа называется бесконечной. Определение 18. Порядком конечной группы G называется число элементов группы G, и обозначается | G |. Определение группы можно сформулировать следующим образом: Определение 13'. Непустое множество G с определённой на нём бинарной алгебраической операцией ∘ называется группой, если выполняются следующие аксиомы:
1)' а ∘(b ∘ c) = (a ∘ b)∘ c, "a, b, c Î G. 2)' $ e Î G: a ∘ e = a, " a Î G (e – правыйнейтральныйэлемент ). 3)' " a Î G $ a' ÎG: a∘ a' = e (a' – правыйсимметричныйэлемент ). Покажем, что определение 13 и определение 13' равносильны. Доказательство. 1) Пусть выполняются аксиомы 1) – 3). 1)' – 3)'. Действительно, если G удовлетворяет условиям 1) – 3), то G удовлетворяет условиям 1)' – 3)'. 2) Пусть выполняются аксиомы 1)'–3)'. Покажем, что выполняются 1)–3). Аксиома 1) = аксиоме 1)'. Покажем, что выполняется аксиома 3). Достаточно показать, что a '∘ a = e. Пусть (a ')' – симметричный элемент для a ', тогда по аксиоме 3)': a '∘(a ')' = e, тогда a '∘ a = (a '∘ a)∘ a '∘= (a '∘ a)∘(a '∘(a ')') = a '∘(a∘ a ')∘ (a ')' = (a '∘ e)∘ (a ')' = a '∘(a ')' = e. Таким образом a '∘ a = e => выполняется аксиома 3). Покажем, что выполняется аксиома 2). Достаточно показать, что e ∘ a = a. e ∘ a = (a ∘ a ')∘ a = a ∘(a '∘ a) = a ∘ e = a. Таким образом, e ∘ a = a => выполняется аксиома 2). Следовательно, определения 13 и 13' равносильны. ч. т. д. Замечание. Для группы можно также сформулировать ещё одно определение 13'', в котором вместо правых нейтрального и симметричного элементов рассматриваются левые.
Простейшие свойства групп. Пусть G – мультипликативная группа. Тогда справедливы свойства: 1. Применение операции «⋅» к любым n элементам группы G не зависит от расстановки скобок, и значит, их можно опустить. Доказательство следует из теоремы 13. 2. Пусть a и b Î G, тогда уравнение ax = b (1) (ya = b) имеет в G единственное решение: x = a -1 b (y = ba -1). Доказательство. 1) Докажем, что уравнение (1) имеет в G решение. Таккак a Î G то, поопределению 13аксиома 3), $ a-1 Î G, тогда умножим обе части (1) на а -1 слева: ax = b Þ 2) Покажем, что a -1 b – единственное решение уравнения (1). Пусть x 0 – решение уравнения (1) Þ ax 0 = b – верное равенство. Умножим на a -1 слева. x 0 = a -1 b => x = x 0. Свойство доказано. 3. " a, b, c Î G: ac = bc Þ a = b (ca = cb Þ a = b), т. е. в G выполняется закон сокращения. Доказательство проводится домножением обеих частей равенства ac = bc (ca = cb)на с-1 справа (слева). 4. " a, b, Î G: ab = a Þ b = e. Доказательство. Пусть ab = a Þ ab = ae Þ b=e. 5. " a, b, Î G: (ab)-1 = b -1 a -1. Доказательство. Покажем, что b -1 a -1 является обратным элементом для ab: (ab)(b -1 a -1) = a (bb -1) a -1 = aea -1 = aa -1 = e = 1 Þ b -1 a -1 = (ab)-1. 6. Единичный элемент в группе G определяется однозначно, т. е. он единственен. 7. Для каждого элемента группы симметричный элемент единственен. Доказательство следует из теорем 11 и 12. Замечание. Свойства 1 – 7 для аддитивных групп имеют вид: 1) Применение операции + к любым n элементам группы G не зависит от расстановки скобок, и значит, их можно опустить. 2) Уравнение a + x = b имеет единственное решение: x = - a + b. 3) a + c = b + c Þ a = b. 4) a + b = a Þ b = 0. 5) –(a + b) = (-b) + (-a). 6) Нулевой элемент в группе G определяется однозначно, т. е. он единственен. 7) Для каждого элемента группы противоположный элемент единственен.
Виды колец. Определение 27. Кольцо K называется ассоциативным, если операция умножения ассоциативна на K, т.е. Определение 28. Кольцо K называется коммутативным, если операция умножения коммутативна на K, т.е. Определение 29. Кольцо K называется ассоциативно-коммутатитвным, если K - ассоциативное кольцо и коммутативное кольцо.
Определение 30. Кольцо K называется кольцом с единицей, если в K существует единичный элемент, т.е. Определение 31. Элементы а и b кольца K называются делителями нуля, если Определение 32. Ассоциативно-коммутативное кольцо с единицей без делителей нуля называется областью целостности. Простейшие свойства колец. Свойство 1. Для кольца K выполняются все свойства аддитивной группы (см. Замечание 1 из вопроса Простейшие свойства групп) 1-7. Свойство 2. Доказательство Докажем, что Свойство 3. Доказательство Рассмотрим равенство Свойство 4. (правило знаков)
2) 3) Доказательство. 1) 2) 3) Свойство 5. Доказательство.
Свойство 6. Пусть Доказательство. Проведем методом математической индукции по параметру n 1) Пусть 2) Предположим, что утверждение верно при n=k, т.е.
3).Докажем, что утверждение верно при n=k+1, т.е. докажем что
Из 1)-3) по методу математической индукции утверждение верно Свойство 7. Пусть Доказательство.
Доказательство. 1) Необходимость. Пусть H -подкольцо кольца K. Докажем, что выполняются условия 1)-2).Т.к. H -подкольцо кольца K Т.к. H -кольцо 2) Достаточность. Пусть выполняются условия 1)-3).Докажем, что Н подкольцо кольца K. В силу определения 33, достаточно проверить, что Н -кольцо. Т.к. выполняются условия 1) и 2) то по теореме 14 Т.к Определение 34. Отображение кольца K в кольцо K
Замечание1. Определения мономорфизма, эпиморфизма, изоморфизма, эндоморфизма, автоморфизма колец формулируется аналогично соответствующим определениям для групп.
9. Поле. Простейшие свойства полей. Определение 35. Ассоциативно-коммутативное кольцо с единицей, в котором любой ненулевой элемент обратим, называется полем. Определение 35'. Непустое множество Р с определёнными на нём бинарными алгебраическими операциями «+» и «×» называется, если выполняются следующие аксиомы (аксиомы поля).
1. < Р,+> - абелева группа, т. е. а) ассоциативность +, т. е. (а + b) + с = а + (b + с), " а, b, c Î Р; б) $ 0 Î Р: а + 0 = 0 + а = а, " а Î Р; в) " а Î Р, $ (- а) Î Р: а + (- а) = - а + а = 0; г) коммутативность +, т. е. a + b = b + a, " a, b Î P. 2. В Р выполняются дистрибутивные законы, т. е. а) (a + b) · c = ac + bc, " a, b, c Î P – правый дистрибутивный закон; б) c· (a + b) = ca + cb, " a, b, c Î P – левый дистрибутивный закон. 3. < Р #, ⋅> - абелева группа, т. е. а) ассоциативность «‧» ·, т. е. (ab) c = a (bc), " a, b, c Î P #; б) $ 1Î Р #: а ⋅1 = 1⋅ а = а, а Î Р #; в) " а Î Р # ·: $ a -1 Î Р # а ⋅ а -1 = а -1 ⋅а =1; г) коммутативность «‧» ·, т. е. ab = ba, " a, b Î P #. Простейшие свойства полей. Свойство 1. Для поля Р выполняются все простейшие свойства колец (св. 1–7). Свойство 2. В поле нет делителей нуля. Доказательство. Допустим, что $ a, b Î P, а ≠ 0, b ≠ 0, ab = 0 (1). Т. к. b ≠ 0 Þ b Î P # Þ $ b -1Î P#. Умножим обе части (1) на b -1 справа : (ab) b -1 = 0 · b -1Þ a (bb -1) = 0 Þ a = 0, противоречие. Þ в Р нет делителей нуля. Теорема доказана.
Поле комплексных чисел Во множестве действительных чисел неразрешимо уравнение x 2+1=0, поэтому возникает необходимость расширить множество действительных чисел так, чтобы в новом множестве данное уравнение было бы разрешимо. Пусть ℂ=ℝ×ℝ={(a,b)| a,b ∈ℝ} Определение 1. Элементы (a,b) и (c,d) ∈ℂ называются равными, если а = с и b = d. Определение 2. Суммой элементов (a,b) и (c,d) ∈ℂ, называется упорядоченная пара Произведением элементов (a,b) и (c,d) ∈ℂ, называется упорядоченная пара Теорема 1. Множество ℂ с заданными на нем операциями «+» и «⋅» по правилам Доказательство. Из определений следует что заданные на ℂ операции «+» и «⋅» являются алгебраическими, так как ∀(a,b) и (c,d) ∈ℂ, I. Покажем что <ℂ,+>абелева группа. 1), 4) Т.к. сложение элементов из ℂ сводится сложению действительных чисел, а на множестве действительных чисел операция “+” ассоциативна и коммутативна, то операция “+”ассоциативна и коммутативна на ℂ. 2) ∃Ө=(0,0) ∈ℂ такое что ∀(a, b)∈ℂ выполняется: (a, b)+Ө=(a +0, b +0)=(a, b) 3 ) ∀ (a,b) ∈ℂ ∃ (-a,-b) ∈ℂ, такоечто (a,b)+ (-a,-b) =(a-a, b-b)= (0,0)= Ө Из пунктов 1)-4) следует что <ℂ,+>абелева группа. II. Проверим, что в ℂ выполняются дистрибутивные законы 5) ∀ (a1,b1), (a2,b2), (a3,b3) ∈ℂ [(a1,b1)+(a2,b2)] (a3,b3)=(a1+a2,b1+b2 )⋅(a3,b3)= (a1,b1)⋅(a3,b3)+(a2,b2)⋅(a3,b3)=(a1a3-b1b3, a1b3+b1a3)+(a2a3-b2b3, a2b3+b2a3)= (a1a3+a2 a3-b1b3-b2b3, a1b3+b1a3+a2b3+b2a3) (4) Элементы (3) и (4) равны, значит, правый дистрибутивный закон выполняется. Справедливость левого дистрибутивного закона на ℂ следует из коммутативности операции «⋅», см далее аксиому 6). III. Покажем, что <ℂ#,⋅>- абелева группа. 6) Покажем что операция «⋅» коммутативна на ℂ. ∀ (a1,b1), (a2,b2) ∈ℂ (a1,b1)⋅(a2,b2)=(a1a2-b1b2,a1b2+a2b1) (5) (a2,b2)⋅(a1,b1) =(a2a1-b2b1, a2b1+a1b2) (6) (5)=(6), поскольку умножение действительных чисел коммутативно. Следовательно операция «⋅» коммутативна на ℂ.
7) Покажем, что «⋅» ассоциативна на ℂ# , ∀ (a1,b1), (a2,b2), (a3,b3) ∈ℂ # [(a1,b1)⋅(a2,b2)]⋅(a3,b3) = (a1a2-b1b2,a1b2+a2b1)⋅(a3,b3)=((a1a2-b1b2)a3 - (a1b2+a2b1)b3, (a1a2-b1b2)b3+(a1b2+a2b1)a3) (7) (a1,b1)⋅[(a2,b2)⋅(a3,b3)]=(a1,b1)(a2 a3 - b2 b3 , a2 b3+b2 a3)= (7)=(8) в силу дистрибутивных и коммутативных законов на множестве действительных чисел. Следовательно «⋅» ассоциативна на ℂ#. 8) Существование нейтрального элемента относительно операции «⋅», т.е.∃ e =(1,0) ∈ℂ#, такой что ∀(a, b) 9) Существование обратного элемента относительно операции «⋅» на ℂ#, т.е. ∀(a, b) (a, b)(c, d)=(1,0) (ac - bd, ad + bc)=(1,0)
Из пунктов 6)-9) следует что <ℂ#,⋅>- абелева группа. Из пунктов I-III следует, что ℂ- поле. Определение 3. Множество ℂ с заданными на нем операциями «+» и «⋅» по правилам и называется полем комплексных чисел, а его элементы называются комплексными числами. Теорема 2. Множество действительных чисел является подмножеством множества комплексных чисел. Доказательство. Докажем, что множество действительных чисел ℝ изоморфно некоторому подмножеству поля ℂ, а именно, подмножеству вида ℝ1={(a,0)׀ a Зададим отображение 1. Покажем что а)
б)
Из а), б) следует, что 2. Покажем, что a) Покажем, что б) Покажем, что Из 1,2 следует, что Теорема 3. В поле ℂ уравнение x2+1=0 разрешимо. Доказательство. Рассмотрим x 2+1=0 как уравнение с коэффициентами из ℂ. А именно, согласно теореме 2, отождествим 1 Отметим что i= (0,1) не принадлежит множеству ℝ1={(a,0)׀ a Определение 4. Мнимой единицей называетсякорень i уравнения x 2+1=0, т.е. число, удовлетворяющее условию i 2=-1.
Глава II. Алгебры. Алгебраические системы. 1. Операции на множествах. Под операциями на множестве М понимают правило или закон, по которому выполняются некоторые действия над элементами множества М. Пример. Операции Под бинарной операцией на множестве М понимают правило или закон, по которому выполняется некоторое действие над двумя элементами множества М; под унарной операцией на множестве М понимают правило или закон, по которому выполняется некоторое действие над одним элементом из М. Пример. В общем случае результат выполнения операции на множестве М не обязан принадлежать множеству М. Пример. На множестве ℕ: 3-5 В общем случае результат выполнения операции не обязан определяться однозначно. Пример. « ∘» на ℕ a ∘ b = a Операции на множествах, для которых результат определяется однозначно и принадлежит исходному множеству, называются алгебраическими. Определение 1. Бинарной алгебраической операцией на множестве М называется отображение Вместо Пример. «+»: а + b = с. Определение 2. Непустое множество М с определенными на нем алгебраическими операциями и отношениями называется алгебраической системой.
Тогда полученную алгебраическую систему обозначают < M, Пример. <ℤ, {+, ⋅}, { Определение 3. Непустое множество с определенными на нем алгебраическими операциями называется алгеброй. Из определений 2 и 3 Пример. < Z, {+,⋅}> - алгебра. Определение 4. Алгебра < М, ∘ > называется группоидом, если ∘- бинарная алгебраическая операция. Определение 4’. Непустое множество с определенной на нем бинарной алгебраической операцией называется группоидом.
|
|||||||||
|
Последнее изменение этой страницы: 2016-06-06; просмотров: 669; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.61.88 (0.015 с.) |


 на множестве P (U), операции +, -, ⋅, / на множествах ℕ, ℤ, ℚ,ℝ.
на множестве P (U), операции +, -, ⋅, / на множествах ℕ, ℤ, ℚ,ℝ. - бинарные;
- бинарные;  - унарная.
- унарная. ℕ.
ℕ. b.
b.

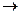
 , которое любым двум элементам a, b из М, необязательно различным, взятым в указанном порядке, ставит в соответствие единственный элемент
, которое любым двум элементам a, b из М, необязательно различным, взятым в указанном порядке, ставит в соответствие единственный элемент  (a, b) из М
(a, b) из М 1 – совокупность некоторых алгебраических операций на множестве М
1 – совокупность некоторых алгебраических операций на множестве М 
 .
.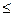 }> - алгебраическая система.
}> - алгебраическая система. алгебра – частный случай алгебраической системы, когда W2 отсутствует.
алгебра – частный случай алгебраической системы, когда W2 отсутствует.
 .
.
 .
. 1
1 
 .
. но
но  .
.
 , т.е. что а это противоположный элемент –а. Действительно,
, т.е. что а это противоположный элемент –а. Действительно, 
 т.е. в K выполняется дистрибутивность умножения относительно разности
т.е. в K выполняется дистрибутивность умножения относительно разности Þ
Þ 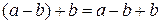 Þ
Þ 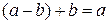 Þ
Þ  Þ
Þ 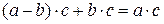 Þ
Þ 
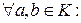 1)
1) 

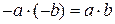


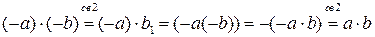




 Тогда
Тогда  Аналогично
Аналогично 
 верно, т.к. K – кольцо.
верно, т.к. K – кольцо.
 Действительно,
Действительно,  =
=

 .
. Тогда
Тогда 

 H -кольцо
H -кольцо  H -аддитивная абелева группа
H -аддитивная абелева группа 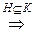 H -подгруппа группы K
H -подгруппа группы K  выполняются условия 1) и 2).
выполняются условия 1) и 2). Н -подгруппа аддитивной группы K Þ Н - аддитивная группа
Н -подгруппа аддитивной группы K Þ Н - аддитивная группа  операция умножения является алгебраической на Н.
операция умножения является алгебраической на Н. и в K выполняется коммутативность сложения и дистрибутивные законы
и в K выполняется коммутативность сложения и дистрибутивные законы  , называется гомоморфным отображением или гомоморфизмом, если выполняются условия:
, называется гомоморфным отображением или гомоморфизмом, если выполняются условия: 

 т. е.
т. е.  (1).
(1). , т. е.
, т. е.  (2).
(2). ℂ# выполняется: (a, b)(1,0)=(a⋅ 1- b⋅ 0, a⋅ 0+ b⋅ 1)=(a, b)
ℂ# выполняется: (a, b)(1,0)=(a⋅ 1- b⋅ 0, a⋅ 0+ b⋅ 1)=(a, b) (по определению равенства элементов)
(по определению равенства элементов)  ,
,  . Вычитая уравнения почленно, получим - b2d-a2d=b;-d(a2+b2)=b;
. Вычитая уравнения почленно, получим - b2d-a2d=b;-d(a2+b2)=b; ∈ℝ. Аналогично, исключая неизвестную d, получим
∈ℝ. Аналогично, исключая неизвестную d, получим  ∈ℝ. Таким образом ∀(a, b) ∈ℂ# существует обратный элемент (
∈ℝ. Таким образом ∀(a, b) ∈ℂ# существует обратный элемент (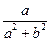 ,
,  )∈ℂ#
)∈ℂ# (a + b,0);
(a + b,0);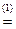 (a+b,0). Значит,
(a+b,0). Значит,  (ab-0,0+0)=(ab,0). Значит,
(ab-0,0+0)=(ab,0). Значит,  (a,0)=(b,0)
(a,0)=(b,0)  ℝ1. Учитывая, что ℝ1Íℂ, можно считать, что ℝ изоморфно вкладывается в ℂ, отожествляя число a ∈ℝ с парой (a,0)∈ℝ1, т.е. (a,0)
ℝ1. Учитывая, что ℝ1Íℂ, можно считать, что ℝ изоморфно вкладывается в ℂ, отожествляя число a ∈ℝ с парой (a,0)∈ℝ1, т.е. (a,0)  a, и можем считать что ℝÍℂ.
a, и можем считать что ℝÍℂ.


