
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Подкольцо. Критерий подколец. Гомоморфизмы и изоморфизмы колец.Содержание книги
Поиск на нашем сайте
Определение 33. Непустое подмножество H кольца K называется подкольцом кольца K, если H является кольцом относительно тех же операций, что и кольцо K. Пример: ℤ- подкольцо кольца ℚ, ℤ- подкольцо кольца ℝ, ℚ- подкольцо кольца ℝ Теорема 15. Пусть H ≠ Æ, H Í K, K – кольцо. H – подкольцо кольца K Û выполняются условия 1). 2). 3). Доказательство. 1) Необходимость. Пусть H -подкольцо кольца K. Докажем, что выполняются условия 1)-2).Т.к. H -подкольцо кольца K Т.к. H -кольцо 2) Достаточность. Пусть выполняются условия 1)-3).Докажем, что Н подкольцо кольца K. В силу определения 33, достаточно проверить, что Н -кольцо. Т.к. выполняются условия 1) и 2) то по теореме 14 Т.к Определение 34. Отображение кольца K в кольцо K
Замечание1. Определения мономорфизма, эпиморфизма, изоморфизма, эндоморфизма, автоморфизма колец формулируется аналогично соответствующим определениям для групп.
9. Поле. Простейшие свойства полей. Определение 35. Ассоциативно-коммутативное кольцо с единицей, в котором любой ненулевой элемент обратим, называется полем. Определение 35'. Непустое множество Р с определёнными на нём бинарными алгебраическими операциями «+» и «×» называется, если выполняются следующие аксиомы (аксиомы поля). 1. < Р,+> - абелева группа, т. е. а) ассоциативность +, т. е. (а + b) + с = а + (b + с), " а, b, c Î Р; б) $ 0 Î Р: а + 0 = 0 + а = а, " а Î Р; в) " а Î Р, $ (- а) Î Р: а + (- а) = - а + а = 0; г) коммутативность +, т. е. a + b = b + a, " a, b Î P. 2. В Р выполняются дистрибутивные законы, т. е. а) (a + b) · c = ac + bc, " a, b, c Î P – правый дистрибутивный закон; б) c· (a + b) = ca + cb, " a, b, c Î P – левый дистрибутивный закон. 3. < Р #, ⋅> - абелева группа, т. е. а) ассоциативность «‧» ·, т. е. (ab) c = a (bc), " a, b, c Î P #; б) $ 1Î Р #: а ⋅1 = 1⋅ а = а, а Î Р #; в) " а Î Р # ·: $ a -1 Î Р # а ⋅ а -1 = а -1 ⋅а =1; г) коммутативность «‧» ·, т. е. ab = ba, " a, b Î P #. Простейшие свойства полей. Свойство 1. Для поля Р выполняются все простейшие свойства колец (св. 1–7). Свойство 2. В поле нет делителей нуля. Доказательство. Допустим, что $ a, b Î P, а ≠ 0, b ≠ 0, ab = 0 (1). Т. к. b ≠ 0 Þ b Î P # Þ $ b -1Î P#. Умножим обе части (1) на b -1 справа : (ab) b -1 = 0 · b -1Þ a (bb -1) = 0 Þ a = 0, противоречие. Þ в Р нет делителей нуля. Теорема доказана.
Подполе. Критерий подполя. Изоморфизмы полей. Определение 36. Непустое подмножество Н поля Р называется подполем поля Р, если Н является полем относительно тех же операций, что и поле Р. Теорема 16 (критерий подполя). Пусть Н ≠ Æ, Н Í Р, Р – поле. Н – подполе поля РÛ выполняются условия: 1). 2). 3). 4). Доказательство. 1. Необходимость. Пусть Н – подполе поля Р Þ Н – поле Þ Н - аддитивная группа Þ выполняется 1) и 2). Н # - мультипликативная группа Þ выполняется 3) и 4). 2. Достаточность. Пусть выполняются условия 1)-4).Покажем, что Н – подполе поля Р. Достаточно показать, что Н –поле. Из 1) и 2) Þ Н – подгруппа аддитивной группы Р Þ Н – аддитивная группа. Из 3) и 4) Þ Н # - подгруппа мультипликативной группы P #Þ Н # - мультипликативная группа. Т. к. Н Í Р и в Р выполняются дистрибутивные законы, коммутативность «+» и «×» Þ в Н выполняются дистрибутивные законы, коммутативность «+» и «×». Таким образом, Н – поле Þ Н – подполе поля Р. Определение 37. Поля Р и Р1 называются изоморфными, обозначаются Р @ Р1, если они изоморфны как кольца.
Поле комплексных чисел Во множестве действительных чисел неразрешимо уравнение x 2+1=0, поэтому возникает необходимость расширить множество действительных чисел так, чтобы в новом множестве данное уравнение было бы разрешимо. Пусть ℂ=ℝ×ℝ={(a,b)| a,b ∈ℝ} Определение 1. Элементы (a,b) и (c,d) ∈ℂ называются равными, если а = с и b = d. Определение 2. Суммой элементов (a,b) и (c,d) ∈ℂ, называется упорядоченная пара Произведением элементов (a,b) и (c,d) ∈ℂ, называется упорядоченная пара Теорема 1. Множество ℂ с заданными на нем операциями «+» и «⋅» по правилам Доказательство. Из определений следует что заданные на ℂ операции «+» и «⋅» являются алгебраическими, так как ∀(a,b) и (c,d) ∈ℂ, I. Покажем что <ℂ,+>абелева группа. 1), 4) Т.к. сложение элементов из ℂ сводится сложению действительных чисел, а на множестве действительных чисел операция “+” ассоциативна и коммутативна, то операция “+”ассоциативна и коммутативна на ℂ. 2) ∃Ө=(0,0) ∈ℂ такое что ∀(a, b)∈ℂ выполняется: (a, b)+Ө=(a +0, b +0)=(a, b) 3 ) ∀ (a,b) ∈ℂ ∃ (-a,-b) ∈ℂ, такоечто (a,b)+ (-a,-b) =(a-a, b-b)= (0,0)= Ө Из пунктов 1)-4) следует что <ℂ,+>абелева группа. II. Проверим, что в ℂ выполняются дистрибутивные законы 5) ∀ (a1,b1), (a2,b2), (a3,b3) ∈ℂ [(a1,b1)+(a2,b2)] (a3,b3)=(a1+a2,b1+b2 )⋅(a3,b3)= (a1,b1)⋅(a3,b3)+(a2,b2)⋅(a3,b3)=(a1a3-b1b3, a1b3+b1a3)+(a2a3-b2b3, a2b3+b2a3)= (a1a3+a2 a3-b1b3-b2b3, a1b3+b1a3+a2b3+b2a3) (4) Элементы (3) и (4) равны, значит, правый дистрибутивный закон выполняется. Справедливость левого дистрибутивного закона на ℂ следует из коммутативности операции «⋅», см далее аксиому 6). III. Покажем, что <ℂ#,⋅>- абелева группа. 6) Покажем что операция «⋅» коммутативна на ℂ. ∀ (a1,b1), (a2,b2) ∈ℂ (a1,b1)⋅(a2,b2)=(a1a2-b1b2,a1b2+a2b1) (5) (a2,b2)⋅(a1,b1) =(a2a1-b2b1, a2b1+a1b2) (6) (5)=(6), поскольку умножение действительных чисел коммутативно. Следовательно операция «⋅» коммутативна на ℂ. 7) Покажем, что «⋅» ассоциативна на ℂ# , ∀ (a1,b1), (a2,b2), (a3,b3) ∈ℂ # [(a1,b1)⋅(a2,b2)]⋅(a3,b3) = (a1a2-b1b2,a1b2+a2b1)⋅(a3,b3)=((a1a2-b1b2)a3 - (a1b2+a2b1)b3, (a1a2-b1b2)b3+(a1b2+a2b1)a3) (7) (a1,b1)⋅[(a2,b2)⋅(a3,b3)]=(a1,b1)(a2 a3 - b2 b3 , a2 b3+b2 a3)= (7)=(8) в силу дистрибутивных и коммутативных законов на множестве действительных чисел. Следовательно «⋅» ассоциативна на ℂ#. 8) Существование нейтрального элемента относительно операции «⋅», т.е.∃ e =(1,0) ∈ℂ#, такой что ∀(a, b) 9) Существование обратного элемента относительно операции «⋅» на ℂ#, т.е. ∀(a, b) (a, b)(c, d)=(1,0) (ac - bd, ad + bc)=(1,0)
Из пунктов 6)-9) следует что <ℂ#,⋅>- абелева группа. Из пунктов I-III следует, что ℂ- поле. Определение 3. Множество ℂ с заданными на нем операциями «+» и «⋅» по правилам и называется полем комплексных чисел, а его элементы называются комплексными числами. Теорема 2. Множество действительных чисел является подмножеством множества комплексных чисел. Доказательство. Докажем, что множество действительных чисел ℝ изоморфно некоторому подмножеству поля ℂ, а именно, подмножеству вида ℝ1={(a,0)׀ a Зададим отображение 1. Покажем что а)
б)
Из а), б) следует, что 2. Покажем, что a) Покажем, что б) Покажем, что Из 1,2 следует, что Теорема 3. В поле ℂ уравнение x2+1=0 разрешимо. Доказательство. Рассмотрим x 2+1=0 как уравнение с коэффициентами из ℂ. А именно, согласно теореме 2, отождествим 1 Отметим что i= (0,1) не принадлежит множеству ℝ1={(a,0)׀ a Определение 4. Мнимой единицей называетсякорень i уравнения x 2+1=0, т.е. число, удовлетворяющее условию i 2=-1.
|
||||
|
Последнее изменение этой страницы: 2016-06-06; просмотров: 2362; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.118.214 (0.007 с.) |

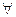 h1, h2
h1, h2  H: h1 + h2
H: h1 + h2  H -кольцо
H -кольцо  H -аддитивная абелева группа
H -аддитивная абелева группа 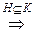 H -подгруппа группы K
H -подгруппа группы K  выполняются условия 1) и 2).
выполняются условия 1) и 2). выполняется условие 3)
выполняется условие 3) Н -подгруппа аддитивной группы K Þ Н - аддитивная группа
Н -подгруппа аддитивной группы K Þ Н - аддитивная группа  операция умножения является алгебраической на Н.
операция умножения является алгебраической на Н. и в K выполняется коммутативность сложения и дистрибутивные законы
и в K выполняется коммутативность сложения и дистрибутивные законы  , называется гомоморфным отображением или гомоморфизмом, если выполняются условия:
, называется гомоморфным отображением или гомоморфизмом, если выполняются условия: 

 т. е.
т. е.  (1).
(1). , т. е.
, т. е.  (2).
(2). (по определению равенства элементов)
(по определению равенства элементов)  ,
,  . Вычитая уравнения почленно, получим - b2d-a2d=b;-d(a2+b2)=b;
. Вычитая уравнения почленно, получим - b2d-a2d=b;-d(a2+b2)=b; ∈ℝ. Аналогично, исключая неизвестную d, получим
∈ℝ. Аналогично, исключая неизвестную d, получим  ∈ℝ. Таким образом ∀(a, b) ∈ℂ# существует обратный элемент (
∈ℝ. Таким образом ∀(a, b) ∈ℂ# существует обратный элемент (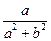 ,
,  )∈ℂ#
)∈ℂ# :ℝ
:ℝ 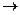 ℝ1, по правилу ∀ a
ℝ1, по правилу ∀ a  (a + b,0);
(a + b,0);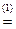 (a+b,0). Значит,
(a+b,0). Значит,  (ab-0,0+0)=(ab,0). Значит,
(ab-0,0+0)=(ab,0). Значит,  (a,0)=(b,0)
(a,0)=(b,0)  ℝ1. Учитывая, что ℝ1Íℂ, можно считать, что ℝ изоморфно вкладывается в ℂ, отожествляя число a ∈ℝ с парой (a,0)∈ℝ1, т.е. (a,0)
ℝ1. Учитывая, что ℝ1Íℂ, можно считать, что ℝ изоморфно вкладывается в ℂ, отожествляя число a ∈ℝ с парой (a,0)∈ℝ1, т.е. (a,0)  a, и можем считать что ℝÍℂ.
a, и можем считать что ℝÍℂ.


