
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Подгруппы. Критерий подгруппы.Содержание книги Поиск на нашем сайте
Определение 19. Непустое подмножество Н группы G называется подгруппой группы G, если Н является группой относительно той же операции, что и группа G, и обозначается Н £ G (Н – подгруппа группы G). Определение 20. Если Н £ G и H Замечание 1. Любая группа G имеет следующие подгруппы: G £ G, Определение 21. Подгруппы Е и G группы G называются тривиальными подгруппами группы G. Все остальные подгруппы группы G нетривиальными или собственными. Теорема 14 (Критерий подгруппы). Пусть Н – непустое множество, Н Í G, G – группа (мультипликативная группа). Н £ G 1) 2) Доказательство: 1. Необходимость: Пусть Н £ G. Покажем, что выполняются условия 1) -2). Так как Н £ G 2. Достаточность: Пусть выполняются условия 1) и 2). Докажем, что Н £ G. В силу определения подгруппы достаточно показать, что Н – непустое множество, Н По условию, Н – непустое множество и Н Достаточно показать, что Н удовлетворяет определению группы. Из условия 1) а). Так как H б). Так как Н – непустое множество в). Из условия 2) Вывод: из а) – в) Теорема 14’ (критерий подгруппы в аддитивной записи) Пусть Н – непустое множество, Н Í G. Н£ G 2). Замечание 2. Критерий подгруппы можно использовать также в следующем виде: Замечание 3. Алгебраическая операция вычитания в группе <G, + > определяется по правилу Гомоморфизмы и изоморфизмы групп. Определение 22. Пусть < G, ∘ >, < G1, * > - группы. Отображение Определение 23. Инъективный гомоморфизм называется мономорфизмом. Сюръективный гомоморфизм называется эпиморфизмом. Биективный – изоморфизмом. Гомоморфизм группы G в G называется эндоморфизмом. Изоморфизм группы G на G называется автоморфизмом.
1 изоморфизм
3 автоморфизм
эндоморфизм где 1 - Определение 24. Взаимно однозначное отображение группы G на G 1 называется изоморфизмом, если Определение 25. Группы G и G 1 называются изоморфными, и обозначаются G Замечание.
Кольцо. Виды колец. Простейшие свойства колец. Определение 26. Непустое множество K с определенными на нем бинарными алгебраическими операциями сложения и умножения называется кольцом, если выполняются следующие аксиомы (аксиомы кольца): 1.< K, +> абелева группа, т.е. а) ассоциативность сложения на K: б) в) г) Операция «+» коммутативна на K: 2.В K выполняются дистрибутивные законы, т.е. а) б) Примеры: ℕ-не является кольцом, т. к. ℕ не явл. аддитивной группой. ℤ-кольцо, ℚ,ℝ-кольца. Виды колец. Определение 27. Кольцо K называется ассоциативным, если операция умножения ассоциативна на K, т.е. Определение 28. Кольцо K называется коммутативным, если операция умножения коммутативна на K, т.е. Определение 29. Кольцо K называется ассоциативно-коммутатитвным, если K - ассоциативное кольцо и коммутативное кольцо. Определение 30. Кольцо K называется кольцом с единицей, если в K существует единичный элемент, т.е. Определение 31. Элементы а и b кольца K называются делителями нуля, если Определение 32. Ассоциативно-коммутативное кольцо с единицей без делителей нуля называется областью целостности. Простейшие свойства колец. Свойство 1. Для кольца K выполняются все свойства аддитивной группы (см. Замечание 1 из вопроса Простейшие свойства групп) 1-7. Свойство 2. Доказательство Докажем, что Свойство 3. Доказательство Рассмотрим равенство Свойство 4. (правило знаков)
2) 3) Доказательство. 1) 2) 3) Свойство 5. Доказательство.
Свойство 6. Пусть Доказательство. Проведем методом математической индукции по параметру n 1) Пусть 2) Предположим, что утверждение верно при n=k, т.е.
3).Докажем, что утверждение верно при n=k+1, т.е. докажем что
Из 1)-3) по методу математической индукции утверждение верно Свойство 7. Пусть Доказательство.
|
||||
|
Последнее изменение этой страницы: 2016-06-06; просмотров: 2785; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.006 с.) |

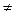 G, то Н называется подгруппой группы G собственно содержащейся в G,и обозначается H < G.
G, то Н называется подгруппой группы G собственно содержащейся в G,и обозначается H < G.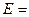
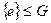 , где Е – единичная подгруппа группы G.
, где Е – единичная подгруппа группы G. выполняются два условия:
выполняются два условия: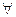 h1, h2
h1, h2  H: h1 ‧ h2
H: h1 ‧ h2  H - группа
H - группа 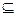 G, H -группа относительно умножения, заданного в G.
G, H -группа относительно умножения, заданного в G. h
h  Пусть Н – непустое множество, Н
Пусть Н – непустое множество, Н  G
G 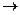 G 1 называется гомоморфным отображением, если
G 1 называется гомоморфным отображением, если 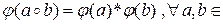 G.
G.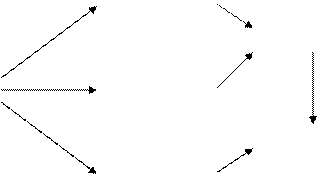 мономорфизм
мономорфизм -гомоморфизм 2 эпиморфизм
-гомоморфизм 2 эпиморфизм G 1, если существует изоморфизм G на G 1.
G 1, если существует изоморфизм G на G 1.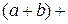 с =
с = 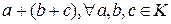
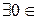 K:
K: 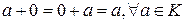

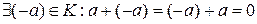
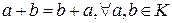
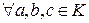
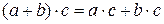 - правый дистрибутивный закон
- правый дистрибутивный закон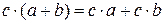 -левый дистрибутивный закон
-левый дистрибутивный закон
 .
.
 .
.
 но
но  .
.
 , т.е. что а это противоположный элемент –а. Действительно,
, т.е. что а это противоположный элемент –а. Действительно, 
 т.е. в K выполняется дистрибутивность умножения относительно разности
т.е. в K выполняется дистрибутивность умножения относительно разности Þ
Þ 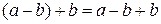 Þ
Þ 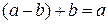 Þ
Þ  Þ
Þ 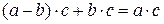 Þ
Þ 
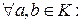 1)
1) 

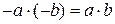


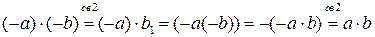




 Тогда
Тогда  Аналогично
Аналогично 
 верно, т.к. K – кольцо.
верно, т.к. K – кольцо.
 Действительно,
Действительно,  =
=

 .
. Тогда
Тогда 




