
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 2. Основы алгебры логикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Основы алгебры логики были заложены в середине XIX века трудами английского математика Дж. Буля, по имени которого она называется также булевой алгеброй. Понимание принципов, лежащих в ее основе, важно для овладения методами описания и проектирования цифровых устройств. Начало использованию алгебры логики для синтеза переключательных (релейных) схем было положено в 1938 г. работами американского ученого К. Шеннона. Аксиомы алгебры логики. В алгебре логики рассматриваются переменные, которые могут принимать только два значения – 0 и 1. В дальнейшем переменные будем обозначать латинскими буквами (при необходимости с цифровыми индексами): x, y, B, А2 и т.п. В алгебре логики определены отношение эквивалентности (=) и три операции: дизъюнкция (операция ИЛИ, логическое сложение), обозначаемая знаком Ú (например, х Ú Y); конъюнкция (операция И, логическое умножение), обозначаемая знаками Ù, & или точкой, которую можно опускать (например, х · А3 = х А3); и отрицание (операция НЕ, инверсия), обозначаемое чертой над переменными или над элементами 0 и 1 (например, Отношение эквивалентности удовлетворяет следующим свойствам: x = х – рефлексивность; если х = y, то y = x – симметричность; если x = y и y = z, то x = z – транзитивность. Из отношения эквивалентности следует принцип подстановки: если X = Y, то в любой формуле, содержащей х, вместо х можно подставить Y, и в результате будет получена эквивалентная формула. Алгебра логики определяется следующей системой аксиом:
Аксиома (2.1) является утверждением того, что в алгебре логики рассматриваются только двоичные переменные, аксиомы (2.2), (2.3) определяют свойства операций дизъюнкции и конъюнкции, а аксиома (2.4) – операции отрицания. Законы, тождества и теоремы алгебры логики. С помощью аксиом алгебры логики можно доказать целый ряд тождеств и теорем. Одним из эффективных методов доказательства теорем является метод перебора всех значений переменных: если теорема истинна, то с учетом (2.2)…(2.4) уравнение, формулирующее утверждение теоремы, должно быть истинно при подстановке любых значений переменных в обе его части. Метод перебора не слишком трудоемок, так как переменные могут иметь только два значения: 0 и 1. Если в логическое выражение входят операции дизъюнкции и конъюнкции, то следует соблюдать следующий порядок выполнения операций: сначала выполняется операция конъюнкции (она имеет приоритет), затем операция дизъюнкции. В сложных логических выражениях для задания иного порядка выполнения операций используются скобки. Операции логического сложения (дизъюнкции) и логического умножения (конъюнкции) для случая одной переменной x обладают следующими свойствами:
Для случая двух и более переменных справедливы следующие законы: переместительные (коммутативные)
сочетательные (ассоциативные):
распределительные (дистрибутивные):
двойственности (теоремы де Моргана):
двойного отрицания:
поглощения:
операции склеивания:
операции обобщенного склеивания:
Некоторые законы и тождества алгебры логики имеют особое значение, так как позволяют упрощать логические выражения. Например, в выражениях (2.5), (2.6), (2.11)…(2.15) правая часть выражения проще левой, поэтому проведя в логических выражениях соответствующие преобразования можно добиться существенного их упрощения. Наиболее часто для преобразования логических выражений с целью их упрощения используются тождества (2.12)…(2.15). Операция сложения по модулю 2 (исключающее ИЛИ, логическая неравнозначность) обозначается символом Å и определяется соотношением:
Используя аксиомы алгебры логики, легко убедиться, что
0 Å 0 = 1 Å 1 = 0; 1 Å 0 = 0 Å 1 = 1. (2.16)
Из этих соотношений следует, что значение x Å y: - совпадает со значением младшего разряда суммы двух одноразрядных двоичных чисел x и y; - совпадает с результатом дизъюнкции переменных x и y, за исключением случая, когда две переменные равны 1 - равно 1 когда значения переменных не равны друг другу. Перечисленные свойства операции x Å y и определяет ее названия. Операция суммирования по модулю 2 коммутативна, ассоциативна и дистрибутивна относительно операции конъюнкции:
Для операции сложения по модулю два также справедливы следующие тождества:
Логические функции. Любое логическое выражение, составленное из n переменных xn,..., x 1 с помощью конечного числа операций алгебры логики, можно рассматривать как некоторую функцию n переменных. В соответствии с аксиомами (2.1)…(2.4) функция может принимать в зависимости от значений переменных только два значения: 0 и 1. Такие функции являются весьма удобным инструментом для описания, анализа и синтеза логических схем, выходные сигналы которых характеризуются лишь двумя уровнями напряжения: высоким (1) и низким (0). В связи с этим логические функции называются переключательными. Для функций n переменных xn,..., x 1 используется общее обозначение F (ν) = F (xn,..., x 1), где ν = (xn,..., x 1), т.е. совокупность переменных xn,..., x 1 можно рассматривать как n -мерный вектор. Так как каждая переменная xp (р = 1, 2,..., n) может принимать только два значения (0 и 1), то число всех возможных комбинаций значений xn,..., x 1 конечно. В общем виде конкретное значение переменной xp (0 или 1) будем обозначать через ep. Областью определения функции n переменных xn,..., x 1 является совокупность точек n -мерного пространства, причем каждая из точек задается определенной комбинацией значений этих переменных:
xn = en ,..., xp = ep ,..., x 1 = e 1,
где eр = 0 или 1 (р = 1, 2,..., n). Обозначим точки, задающие область определения функции F (ν) через
νi = (en,..., ep,... e 1).
Если представить эту комбинацию значений переменных (en,..., ep,... e 1) как число, записанное в двоичном коде, то оказывается возможным пронумеровать все точки области определения логической функции с помощью n -разрядных двоичных чисел (en ... ep... e 1)2 или с помощью эквивалентных им десятичных чисел i. Так как имеется 2 n различных n -разрядных двоичных чисел, то область определения функции n переменных будет содержать 2 n точек:
Для задания функции F (ν) следует указать ее значения во всех точках области определения, т.е. следует задать значения F (ν i) = 0 или 1, где i = 0, 1,..., 2 n – 1. Каждой конкретной функции n переменных можно поставить в соответствие 2 n -разрядное число, составленное из значений F (ν i) = 0 или 1, которые она принимает в 2 n точках области определения. Так как имеется всего Функции n переменных могут зависеть не от всех переменных xn,..., x 1. Такие функции называются вырожденными. В частности, функция F 0(ν), равная нулю, и функция F 1(ν), равная единице во всех точках ν i (i = 0, l,..., 2 n – 1) области определения, не зависят ни от одной переменной. Эти функции называются константой ноль и константой единица соответственно. Функция n переменных F (ν) называется полностью определенной, если ее значения F (ν i) = ai = 0 или 1 заданы во всех 2 n точках ν i области определения. Если же значение функции не задано хотя бы в одной точке ν i, то она называется не полностью определенной. Не определенное в точке ν i значение функции описывается символом сi = * или Ф (Ф – совмещенные символы 0 и 1, что указывает на неопределенность значения функции), т.е., если в точке ν i значение функции не задано, то F (ν i) = сi. Не полностью определенные функции можно доопределять произвольным способом, полагая сi = 0 или 1. Если значения функции не заданы в m точках, то функцию можно доопределить 2 m способами, так как имеется 2 m различных m -разрядных двоичных чисел, соответствующих различным способам доопределения функции в m точках. Таким образом, не определенной в m точках функции соответствует группа из 2 m полностью определенных функций. Так как область определения любой функции n переменных конечна (2 n точек), она может быть задана таблицей значений F (ν i) = ai = 0 или 1 (или сi), которые она принимает в точках ν i, где i = 0, 1,..., 2 n – 1. Такие таблицы называются таблицами истинности. Второй способ задания логической функции – аналитический, при котором функция задается в виде логического выражения, получаемого путем логических преобразований с помощью законов и правил Булевой алгебры. Функции двух переменных F (x 2, x 1). Область определения таких функций состоит из 4 точек (2 n = 22 = 4): ν0 = (0, 0), ν1 = (0, 1), ν2 = (1, 0), ν3 = (1, 1). Общее количество функций двух переменных равно 16 (
Таблица 2.1 – Таблицы истинности функций двух переменных
Каждая функция F 0… F 15 обозначает одну из 16 возможных логических операций над двумя переменными x 1 и x 2, имеет собственное название и аналитическое описание: F 0 = 0 (F 15 = 1) – константа ноль (единица);
Функции двух переменных исключительно важны в силу того, что любая функция n переменных может быть получена из них методом суперпозиции – подстановкой этих функций вместо переменных в другие функции. Такая подстановка возможна на основании того, что области значений функций и переменных совпадают (0 и 1). Наибольшее применение получили следующие невырожденные функции двух переменных х 2 и х 1: F 1 (конъюнкция, И), F 6 (сумма по модулю два, исключающее ИЛИ), F 7 (дизъюнкция, ИЛИ), F 8 (ИЛИ-НЕ) и F 14 (И-НЕ). Принцип и закон двойственности. Алгебра логики обладает замечательным свойством, которое называется принципом двойственности: если имеет место тождество F (ν, 0, 1/ &, Ú) = G (ν, 0, 1/ &, Ú), где ν = (xn,..., x 1), то справедливо также тождество F (ν, 1, 0/ Ú, &) = G (ν, 1, 0/ Ú, &), т.е., если в каком-либо тождестве произвести взаимную замену символов 0 и 1 (если они имеются) и операций дизъюнкции и конъюнкции, то в результате также будет получено тождество. Два тождества, связанные между собой таким образом, называются двойственными. Истинность самого принципа двойственности не доказывается, так как данный принцип является внутренним свойством алгебры логики (заключен в ее аксиомах). Законы двойственности (теоремы де Моргана (2.10)) определяют способ отыскания инверсных функций, представляющих собой дизъюнкцию и конъюнкцию двух переменных. К. Шеннон предложил обобщение этих теорем, позволяющее отыскивать инверсию любой функции F (ν). Закон двойственности имеет вид:
где ν = (xn,..., x 1), Теоремы разложения. В теории логических функций важное значение имеет теорема разложения: любую функцию F (ν) можно разложить по переменной xp в форме
Теорема легко доказывается методом перебора. Используя принцип двойственности можно также записать:
С теоремами разложения связаны тождества:
Первичные термы, минтермы и макстермы. Переменные xp и их инверсии
где eр = 0 или 1. Данное символическое обозначение объединяет в одном символе
Минимальным термом (минтермом, конституентой единицы) называется функция n переменных (конъюнкция первичных термов):
где ν = (xn,..., x 1), eр = 0 или 1, i = (en... e 1)2. Из данного определения следует, что имеется 2 n различных минтермов n переменных, так как имеется 2 n различных n -разрядных двоичных чисел i = 0, 1,…, 2 n– 1. Минтермы обладают следующими свойствами:
Свойство (2.26) соответствует тому, что любой минтерм Ki (ν) равен 1 только в одной точке ν i области определения. Все минтермы двух переменных
Аналогично можно записать минтерм большего числа переменных. Например, пусть n = 4, i = 5 = (0101)2, тогда
Максимальным термом (макстермом, конституентой ноля) называется функция n переменных (дизъюнкция инверсий первичных термов):
где ν = (xn,..., x 1), eр = 0 или 1, i = (en... e 1)2. Макстермы обладают следующими свойствами:
Свойства макстермов могут быть получены из свойств минтермов на основании (2.29). Макстермы – функции, равные 0 только в одной точке ν i области определения, состоящей из 2 n точек. Все макстермы двух переменных
Запишем макстерм
Минтермы (макстермы) представляют собой функции, принимающие минимальное (максимальное) значение из значений своих первичных термов Формы аналитического представления логических функций. Логические функции, которые считаются полностью определенными, при аналитической записи могут быть представлены различными формами. СДНФ – совершенная дизъюнктивная нормальная форма. Теорему разложения (2.20) для функции n переменных можно использовать n раз, т.е. функцию можно разложить по всем n переменным xp, где р = 1, 2,..., n. В качестве примера разложим функцию F (ν) = F (x 2, x 1) двух переменных x 2 и x 1. По теореме разложения получим
где ν i = (e 2, e 1) – i -я точка области определения, i = (e 2 e 1)2; F (ν i) = ai = 0 или 1 – значение функции в i -й точке области определения. Такая форма представления функции двух переменных и называется СДНФ. Разложение функции n переменных будет представлять собой дизъюнкцию 2 n членов вида
Выражение (2.33) представляет собой СДНФ функции n переменных. Так как значения функции ai = 0 или 1, то
где i 1 – номера точек области определения, в которых функция F (ν) равна 1. СДНФ записи функции легко получить по ее таблице истинности. В качестве примера рассмотрим функцию трех переменных x 3, x 2 и x 1, заданной таблицей истинности (таблица 2.2). Из нее следует, что а 0 = а 1= а 4= а 6= 0, а 2 = а 3= а 5= а 7= 1, поэтому
Таблица 2.2 – Таблица истинности функции трех переменных
СКНФ – совершенная конъюнктивная нормальная форма. Такую форму записи функции n переменных F (ν) можно получить на основании двойственной теоремы разложения (2.21). Однако СКНФ можно получить более простым способом – записав СДНФ инверсии функции Тогда на основании (2.33) СДНФ инверсной функции:
Отсюда на основании закона двойственности (2.19) следует
Используя определение макстермов (2.29) получаем СКНФ представления функции n переменных:
Так как значения функции ai = 0 или 1, то
где i 0 – номера точек области определения, в которых функция F (ν) равна 0. Для примера рассмотрим функцию трех переменных x 3, x 2 и x 1, заданной таблицей истинности (см. таблицу 2.2). Так как а 0 = а 1= а 4= а 6= 0, то на основании (2.36) СКНФ функции имеет вид:
Совершенные нормальные формы в базисах И-НЕ и ИЛИ-НЕ. Совокупность элементарных функций, с помощью которых можно записать любую функцию F (ν), называется функционально полной системой функций или базисом. Из выражений (2.34) и (2.36) следует, что для представления любой функции F (ν) в СДНФ и СКНФ достаточно использовать только операции (функции) И, ИЛИ и НЕ (опрерация НЕ нужна для получения первичных термов Преобразуем СДНФ функции (2.33) с использованием закона двойного отрицания и закона двойственности:
Данная форма представления функции называется совершенной нормальной формой (СНФ) в базисе И-НЕ, так как она требует использования только функций И-НЕ. Преобразуем теперь СКНФ функции (2.35) с использованием закона двойного отрицания и закона двойственности:
Данная форма представления функции называется совершенной нормальной формой в базисе ИЛИ-НЕ, так как она требует использования только функций ИЛИ-НЕ. СНФ функции, рассматриваемой в качестве примера, в базисах И-НЕ и ИЛИ-НЕ будут запишутся в виде:
Таким образом, термин “дизъюнктивная (конъюнктивная)” форма представления функции подразумевает, что в логическом выражении, задающем функцию, последняя выполняемая операция – дизъюнкция (конъюнкция), “нормальная” – что в логическом выражении, задающем функцию, последовательно выполняются не более двух операций из совокупности операций И, ИЛИ, И-НЕ, ИЛИ-НЕ, “совершенная” – все минтермы (макстермы), входящие в логическое выражение, имеют одинаковую размерность, т.е. содержат одинаковый набор первичных термов.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 784; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.01 с.) |

 ,
,  ).
).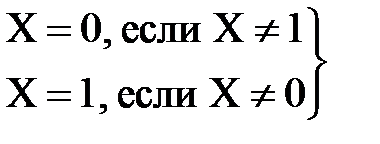 (2.1)
(2.1)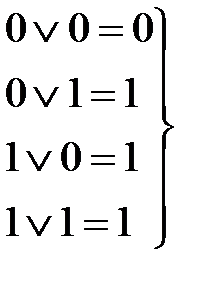 (2.2)
(2.2) (2.3)
(2.3)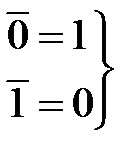 (2.4)
(2.4)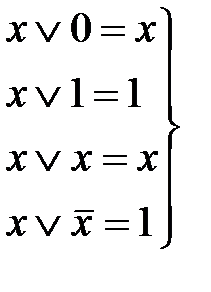 (2.5)
(2.5)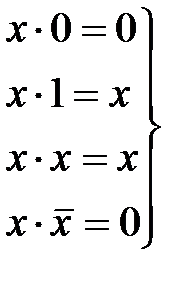 (2.6)
(2.6) , (2.7)
, (2.7)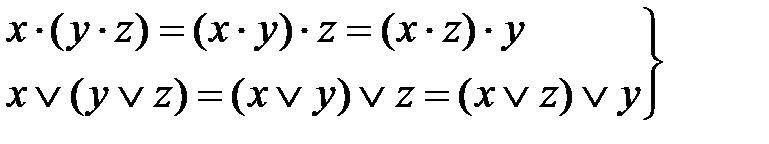 , (2.8)
, (2.8)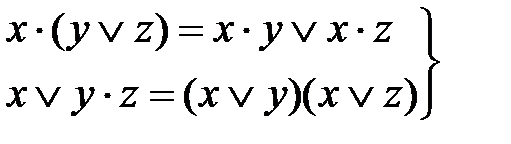 , (2.9)
, (2.9) , (2.10)
, (2.10)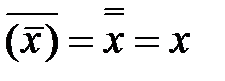 , (2.11)
, (2.11)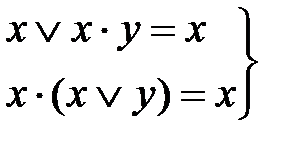 , (2.12)
, (2.12)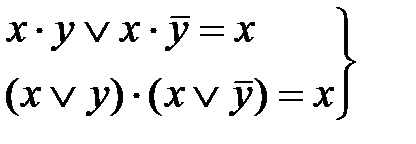 , (2.13)
, (2.13)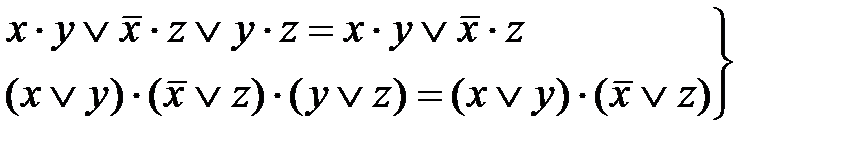 , (2.14)
, (2.14)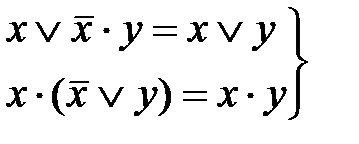 . (2.15)
. (2.15)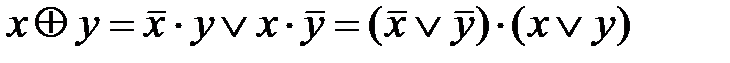 .
.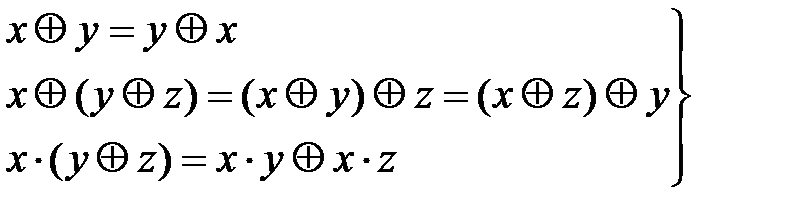 . (2.17)
. (2.17)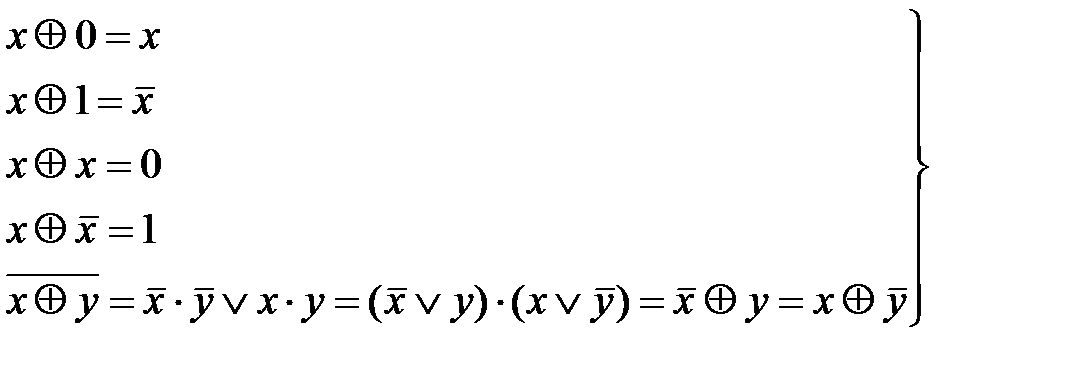 . (2.18)
. (2.18) .
.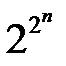 различных 2 n -разрядных двоичных чисел, то и число различных функций n -переменных равно
различных 2 n -разрядных двоичных чисел, то и число различных функций n -переменных равно 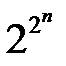 .
.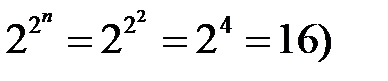 . Значения всех возможных функций F (x 2, x 1) представлены в таблице 2.1, которая представляет собой совмещенную таблицу истинности функций F 0… F 15 двух переменных. В левой части таблицы перечислены все возможные сочетания значений переменных
. Значения всех возможных функций F (x 2, x 1) представлены в таблице 2.1, которая представляет собой совмещенную таблицу истинности функций F 0… F 15 двух переменных. В левой части таблицы перечислены все возможные сочетания значений переменных  и
и 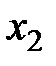 , в правой части приведены значения функций F 0… F 15 при этих сочетаниях переменных.
, в правой части приведены значения функций F 0… F 15 при этих сочетаниях переменных. – конъюнкция, логическое умножение, И;
– конъюнкция, логическое умножение, И; (
( 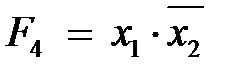 ) – запрет x 1 (x 2);
) – запрет x 1 (x 2);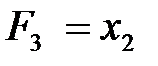 (
( 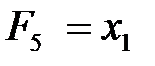 ) – повторение x 2 (x 1);
) – повторение x 2 (x 1); – неэквивалентность, сложение по модулю 2, исключающее ИЛИ;
– неэквивалентность, сложение по модулю 2, исключающее ИЛИ;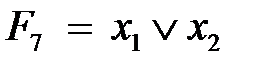 – дизъюнкция, логическое сложение, ИЛИ;
– дизъюнкция, логическое сложение, ИЛИ;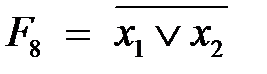 – функция Пирса, ИЛИ-НЕ;
– функция Пирса, ИЛИ-НЕ;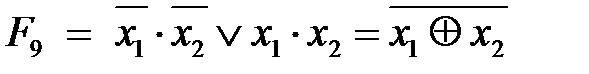 – эквивалентность, исключающее ИЛИ-НЕ;
– эквивалентность, исключающее ИЛИ-НЕ;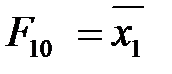 (
(  ) – отрицание x 1 (x 2), инверсия x 1 (x 2), НЕ;
) – отрицание x 1 (x 2), инверсия x 1 (x 2), НЕ;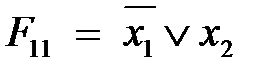 (
( 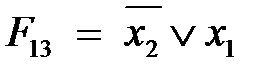 ) – импликация x 1 (x 2);
) – импликация x 1 (x 2); – функция Шеффера, И-НЕ.
– функция Шеффера, И-НЕ.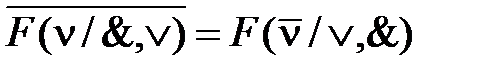 , (2.19)
, (2.19)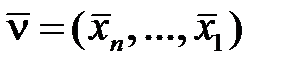 , т.е. инверсию любой функции F (ν) можно получить взаимной заменой переменных xp и их инверсий
, т.е. инверсию любой функции F (ν) можно получить взаимной заменой переменных xp и их инверсий 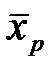 (р = 1, 2,..., n) и операций дизъюнкции и конъюнкции.
(р = 1, 2,..., n) и операций дизъюнкции и конъюнкции.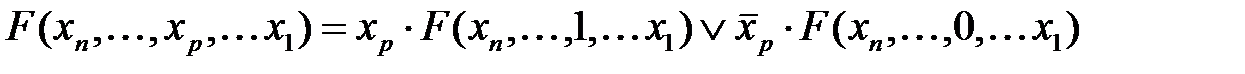 . (2.20)
. (2.20)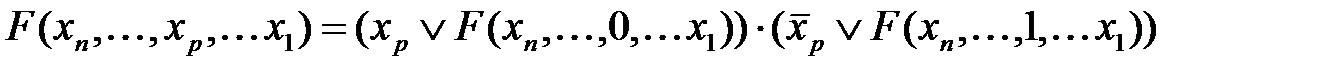 . (2.21)
. (2.21)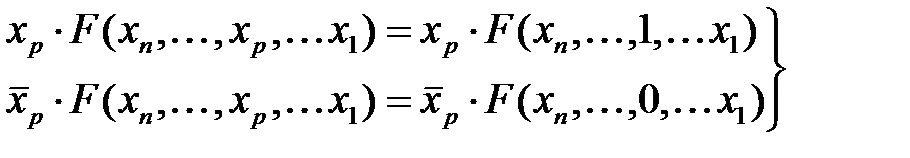 , (2.22)
, (2.22)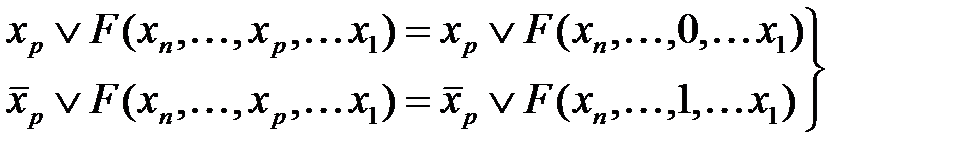 . (2.23)
. (2.23)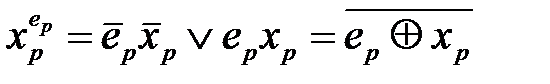 , (2.24)
, (2.24)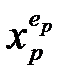 оба первичных терма xp и
оба первичных терма xp и 
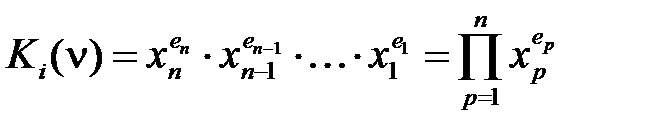 , (2.25)
, (2.25)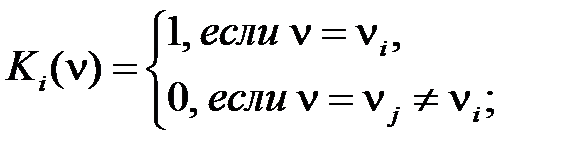 (2.26)
(2.26) ; (2.27)
; (2.27) . (2.28)
. (2.28)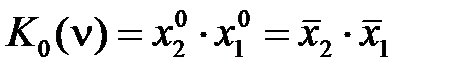 ;
;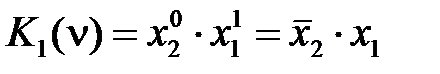 ;
; ;
;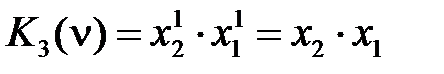 .
. .
.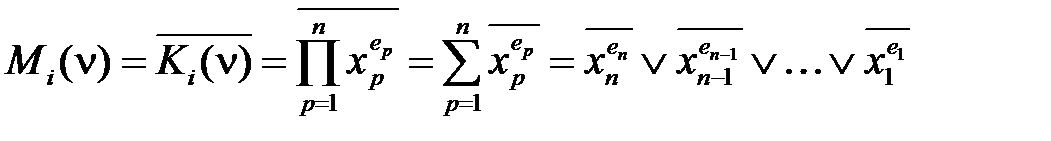 , (2.29)
, (2.29)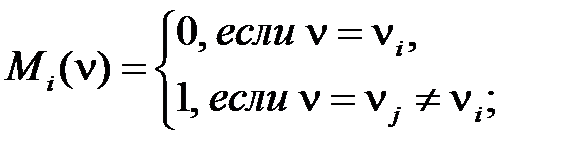 (2.30)
(2.30) ; (2.31)
; (2.31)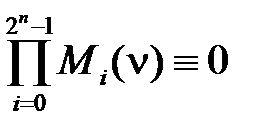 . (2.32)
. (2.32)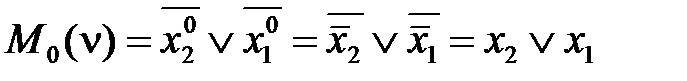 ;
;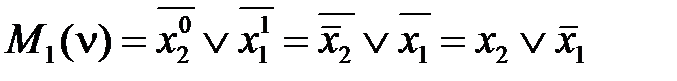 ;
; ;
; .
. для n = 4:
для n = 4: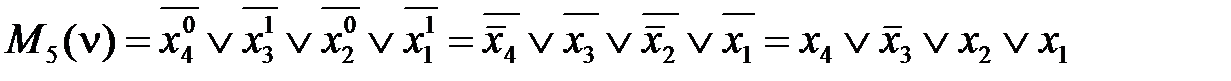 .
.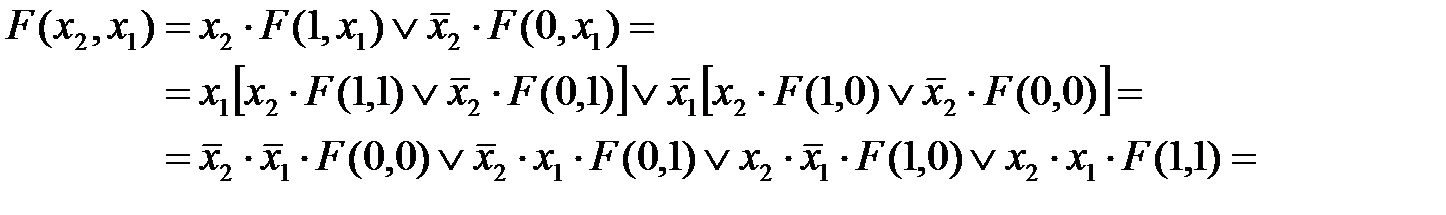
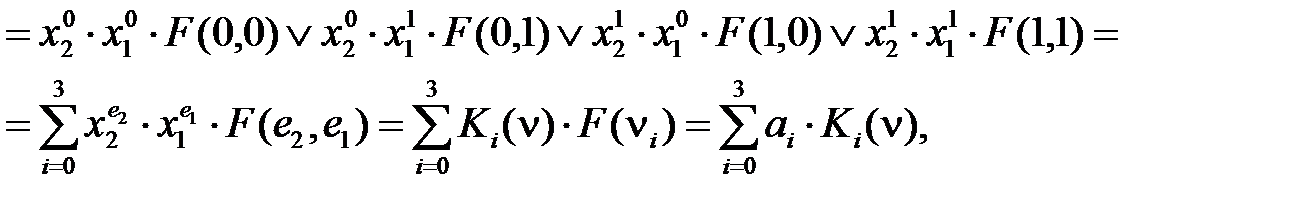
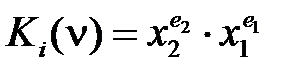 – минтерм двух переменных x 2 и x 1;
– минтерм двух переменных x 2 и x 1; :
: , (2.33)
, (2.33)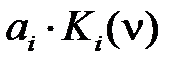 = 0, если ai = 0, и
= 0, если ai = 0, и 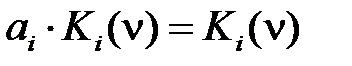 , если ai = 1. Поэтому СДНФ можно представить в виде
, если ai = 1. Поэтому СДНФ можно представить в виде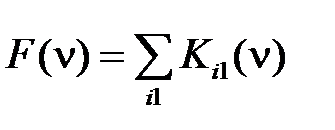 , (2.34)
, (2.34)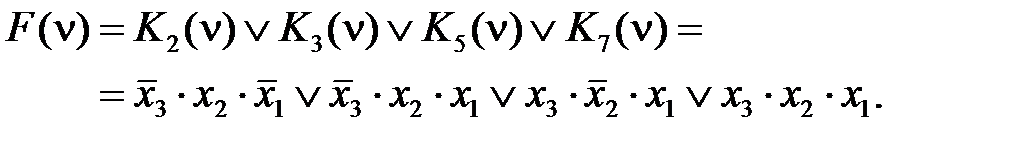
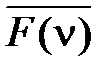 . Инверсная функция в каждой точке ν i области определения имеет инверсные значения
. Инверсная функция в каждой точке ν i области определения имеет инверсные значения 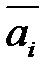 по отношению к значениям ai самой функции, т.е. если F (ν i) = ai, то
по отношению к значениям ai самой функции, т.е. если F (ν i) = ai, то 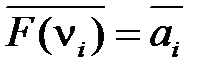 .
.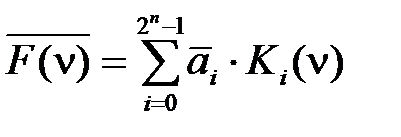 .
. .
.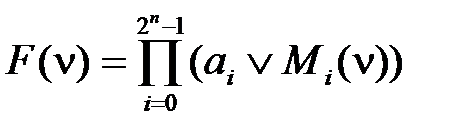 . (2.35)
. (2.35) = 1, если ai = 1, и
= 1, если ai = 1, и  , если ai =. Поэтому СКНФ можно представить в виде
, если ai =. Поэтому СКНФ можно представить в виде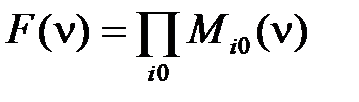 , (2.36)
, (2.36)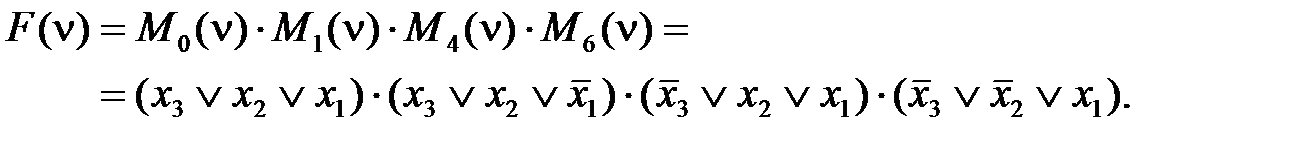
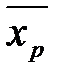 , входящих в минтермы и макстермы), т.е. совокупность этих операций является базисом.
, входящих в минтермы и макстермы), т.е. совокупность этих операций является базисом.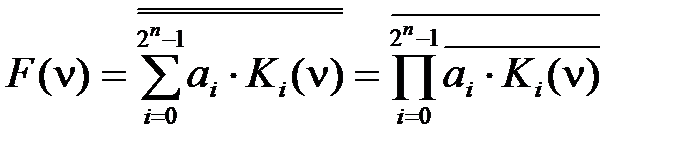 , (2.37)
, (2.37)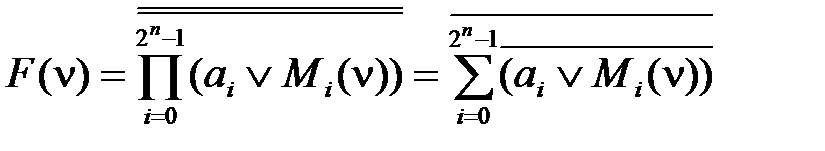 . (2.38)
. (2.38)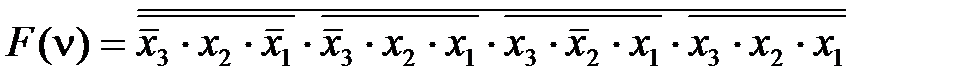 ;
; .
.


