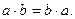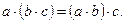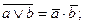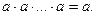Цифровая электроника. Законы алгебры логики. Базовые логические элементы. Таблицы истинности.

В Булевой алгебре, на которой базируется вся цифровая техника, электронные элементы должны выполнять ряд определённых действий. Это так называемый логический базис. Вот три основных действия:

ИЛИ – логическое сложение (дизъюнкция) – OR;

И – логическое умножение (конъюнкция) – AND;

НЕ – логическое отрицание (инверсия) – NOT.

Примем за основу позитивную логику, где высокий уровень будет "1", а низкий уровень примем за "0". Чтобы можно было более наглядно рассмотреть выполнение логических операций, существуют таблицы истинности для каждой логической функции. Сразу нетрудно понять, что выполнение логических функций «и» и «или» подразумевают количество входных сигналов не менее двух, но их может быть и больше.

Логический элемент И.

На рисунке представлена таблица истинности элемента " И " с двумя входами. Хорошо видно, что логическая единица появляется на выходе элемента только при наличии единицы на первом входе и на втором. В трёх остальных случаях на выходе будут нули.

Вход X1	Вход X2	Выход Y

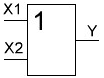
На принципиальных схемах логический элемент "И" обозначают так.

На зарубежных схемах обозначение элемента "И" имеет другое начертание. Его кратко называют AND.

Логический элемент ИЛИ.

Элемент " ИЛИ " с двумя входами работает несколько по-другому. Достаточно логической единицы на первом входе или на втором как на выходе будет логическая единица. Две единицы так же дадут единицу на выходе.

Вход X1	Вход X2	Выход Y

На схемах элемент "ИЛИ" изображают так.

На зарубежных схемах его изображают чуть по-другому и называют элементом OR.

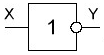
Логический элемент НЕ.

Элемент, выполняющий функцию инверсии «НЕ» имеет один вход и один выход. Он меняет уровень сигнала на противоположный. Низкий потенциал на входе даёт высокий потенциал на выходе и наоборот.

Вход X	Выход Y

Вот таким образом его показывают на схемах.

В зарубежной документации элемент "НЕ" изображают следующим образом. Сокращённо называют его NOT.

Все эти элементы в интегральных микросхемах могут объединяться в различных сочетаниях. Это элементы: И–НЕ, ИЛИ–НЕ, и более сложные конфигурации. Пришло время поговорить и о них.

Основные законы алгебры логики являются двойственными: относительно логического сложения и относительно логического умножения. Ими являются:

1. Переместительный (коммутативный) закон:

- относительно сложения

- относительно умножения

2. Сочетательный (ассоциативный) закон:

- относительно сложения

- относительно умножения

3. Распределительный (дистрибутивный) закон:

- относительно сложения

- относительно умножения

4. Закон инверсии (де Моргана):

- относительно сложения

 

- относительно умножения

5. Закон повторения (идемпотентности):

На основании алгебры логики очевидны следующие соотношения (аксиомы алгебры логики):

Последние соотношения (относительно a) легко доказываются подстановкой вместо a его возможных значений – 0 и 1.

Рассмотренные законы применимы не только к отдельным переменным, но и к группам переменных, объединенных операциями алгебры логики.

В алгебре логики установлен порядок выполнения действий. При отсутствии в выражении скобок первыми должны выполняться операции отрицания (инверсии), затем операции конъюнкции и последними – операции дизъюнкции. При наличии в выражении скобок в первую очередь производятся операции внутри скобок.

При преобразовании логических функций зачастую приходится производить операцию инверсирования их.

Таблица истинности — это таблица, в которой отражены все значения логической функции при всех возможных значениях, входящих в неё логически
Под «логической функцией» в данном случае понимается функция, у которой значения переменных (параметров функции) и значение самой функции выражают логическую истинность. Например, в двузначной логике они могут принимать значения «истина» либо «ложь» (true либо false, 1 либо 0).

Таблицы истинности для основных двоичных логических функций

Конъюнкция Дизъюнкция Импликация Эквиваленция

a

b

a∧b

a

b

a∨b

a

b

a→b

a

b

a↔b

Алгоритм составления таблиц истинности.

1) Подсчитать количество логических переменных n

2) Подсчитать количество строк m=2^n

3) Количество столбцов = n+ количество логических операция

Цифровая электроника

В цифровой электронике используются не непрерывный ток, а импульсы, т.е. для тока возможны только два состояния – сильный ток или слабый. Цифровые схемы используются в электронных устройствах – калькуляторах, часах. Импульсы тока в цифровой схеме могут служить для двоичной записи информации. Двоичный код – это способ записи информации при помощи нулей и единиц. Двоичным кодом можно записывать слова, звуки, изображения. В электронных часах используются цифровые электронные схемы. В цифровых электронных устройствах сильный ток означает единицу, а слабый – нуль.

Электронные устройства меняют направление тока в цифровых схемах. А состоящие из них логические элементы способны производить вычисления. В карманном калькуляторе есть сложные цифровые схемы. Они могут запоминать числа и производить вычисления. Нажимая на кнопки, мы посылаем в схему электронные сигналы.