
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 4. Типовые комбинационные схемыСодержание книги
Поиск на нашем сайте
Физическое устройство, реализующее одну из основных операций алгебры логики или простейшую переключательную функцию, называется логическим элементом (ЛЭ). Схема, составленная из конечного числа ЛЭ по определенным правилам, называется логической схемой (ЛС). Если ЛС полностью описывается переключательными функциями (одной или несколькими), то она называется комбинационной схемой (КС). Таким образом, логическое состояние выходного сигнала КС однозначно определяется текущим логическим состоянием входных сигналов. Комбинационные устройства могут иметь в своем наборе произвольное число логических элементов, при этом выходы одних логических элементов соединяются со входами других. Но в таких схемах нет обратных связей, по которым сигнал с выхода схемы может пройти на ее вход. При наличии цепей обратной связи схема становится последовательностной. В качестве базовых используются ЛЭ, получившие название исходя из реализуемой логической функции: элемент (схема) НЕ, инвертор; элемент (схема) И, конъюнктор; элемент (схема) ИЛИ, дизъюнктор; элемент (схема) И-НЕ; элемент (схема) ИЛИ-НЕ;элемент (схема) исключающее ИЛИ, сумматор по модулю два. Их условные графические изображения представлены на рисунке 4.1. ЛЭ И, ИЛИ, И-НЕ, ИЛИ-НЕ могут иметь более двух входов, реализуя соответствующие логические функции большего числа переменных.
а) б) в) г) д) е)
Рисунок 4.1 – Условные графические обозначения базовых ЛЭ: а – НЕ, б – И, в – ИЛИ, г – И-НЕ, д – ИЛИ-НЕ, е – исключающее ИЛИ.
Проектирование КС осуществляется по этапам: 1. На основании словесной формулировки задачи составляется таблица истинности, задающая значения функции на всех наборах аргументов. 2. По таблице истинности записывается логическое выражение в совершенной дизъюнктивной нормальной форме (СДНФ – сумма минтермов, на которых функция принимает единичное значение). 3. Используя аналитический или табличный метод, производится минимизация логического выражения и записывается ФАЛ в минимальной ДНФ. 4. Используя полученное уравнение в качестве структурной формулы, составляем логическую схему в Булевском базисе И, ИЛИ, НЕ. 5. При необходимости переходим к заданному логическому базису.
6. Синтезируется схема с использованием базовых логических элементов. Наряду с базовыми ЛЭ широкое применение находят типовые КС. Мультиплексоры (multiplexer) – это функциональный узел, который по заданному адресному двоичному коду осуществляет выбор одного из информационных каналов и подключает его к своему выходу. На схемах мультиплексор обозначают буквами МUХ (рисунок 4.2). В общем случае на входы мультиплексора На входы Вход E (enable) разрешает (либо запрещает) работу мультиплексора при подаче на него сигналов управления.
Рисунок 4.2 – Условное графическое обозначение мультиплексора 4 – 1
Таблица 4.1 – Таблица истинности мультиплексора 4 – 1
Согласно данных таблицы 4.1 логическая функция Q, реализуемая мультиплексором 4 – 1, описывается выражением:
Если Построенная по выражению (4.1) схема мультиплексора приведена на рисунке 4.3.
Рисунок 4.3 – Схема мультиплексора
Размерность мультиплексоров в стандартных сериях ИМС не превышает 16 – 1. Для увеличения размерности мультиплексоров осуществляют наращивание нескольких мультиплексоров меньшей разрядности. С помощью мультиплексоров можно решать широкий круг задач, используя их как универсальные логические модули. Демультиплексор осуществляет передачу сигналов с одного информационного входа D на N выходов, имеющих заданный адрес. В общем случае число выходов На рисунке 4.4 показаны условное обозначение демультиплексора 1– 4, и его функционирование описывается его таблицей истинности (таблица 4.2).
Таблица 4.2 - Таблица истинности мультиплексора 4 – 1
Рисунок 4.4 – Условное графическое обозначение демультиплексора 4 – 1
Согласно данных таблицы истинности запишем логическое выражение для каждого выхода демультиплексора и по ним составим логическую схему (рисунок 4.5).
Рисунок 4.5 – Схема демультиплексора 1 – 4
Шифратор (coder) предназначен для преобразования входных сигналов в виде кода "1 из m" в выходной n-разрядный двоичный код и применяется в устройстве ввода информации в цифровые системы. Таким образом классический шифратор преобразует номер возбуждаемого входа (на который подается 1) в двоичный код на своем выходе. Шифратор называется полным, если число входов На рисунке 4.6 показано условное графическое обозначение полного шифратора 8 – 3, а его таблица истинности приведена в таблице 4.3.
Рисунок 4.4 – Условное графическое обозначение шифратора 8 – 3
Таблица 4.3 – Таблица истинности полного шифратора 8 – 3
Согласно данных таблицы 4.3 значения выходных переменных шифратора определяются следующими логическими выражениями:
Необходимо отметить, что шифратор, реализованный по выражениям (4.3), будет правильно работать только в случае подачи на его входы унитарного кода ("1 из m"), т.е. должно выполняться условие Для обработки входного кода, в котором присутствует более одной единицы, т.е. при возбуждении нескольких входов устройства, применяют приоритетный шифратор. В нем выходной код соответствует номеру того возбуждаемого входа, приоритет которого задан более высоким. На схемах приоритетный шифратор обозначается буквами PRCD. Таблица истинности шифратора, приоритет входов которого возрастает с увеличением номера входа, представлена таблицей 4.4.
Таблица 4.4 – Таблица истинности приоритетного шифратора 8 – 3
Состояния выходов такого приоритетного шифратора определяются следующими логическими функциями:
Дешифратор (decoder) выполняет функцию, обратную шифратору, т.е. преобразует входной n -разрядный двоичный код в унитарный ("1 из m "). Таким образом, сигнал логической единицы появится только на том выходе дешифратора, номер которого соответствует десятичному эквиваленту входного двоичного кода. Дешифратор называется полным, если при n входах имеется
Рисунок 4.5 – Условное графическое обозначение дешифратора 3 – 8
Рассмотрим пример синтеза полного дешифратора 3 – 8, имеющего на входе 3-разрядный двоичный код, а на 8 выходах унитарный код. Анализ таблицы истинности (таблица 4.5) такого дешифратора показывает, где каждой выходной функции Q 0… Q 7 соответствует только один минтерм. Так как рассматриваемый дешифратор полный, то он реализует полный набор минтермов входных переменных I 0, I 1, I 2:
Таблица 4.5 – Таблица истинности полного дешифратора 3 – 8
Если комбинационная схема реализует только один минтерм, то ее часто называют дешифратором состояния (кода). Сумматор (summater) – цифровой функциональный узел, выполняющий арифметическое сложение двоичных чисел. На схемах сумматор обозначается буквами SM. Простейшим сумматором является полусумматор HS (half summater), осуществляющий арифметическое сложение двух одноразрядных чисел А и В (рисунок 4.6). Он имеет два выхода – выход S бита суммы и выход P бита переноса в старший разряд. Логика работы полусумматора описывается таблицей 4.6.
Рисунок 4.6 – Условное графическое обозначение полусумматора Таблица 4.6 – Таблица истинности полусумматора
Из таблицы истинности следует, что арифметическая сумма S двух одноразрядных чисел А и В совпадает с суммированием их по модулю два:
Сигнал переноса в старший разряд
Одноразрядный полный сумматор SM (рисунок 4.7) отличается от полусумматора HS тем, что на его дополнительный вход поступает сигнал переноса С от предыдущего разряда сумматора (таблица 4.7).
Рисунок 4.7 – Условное графическое обозначение одноразрядного сумматора
Таблица 4.7 – Таблица истинности полного сумматора
Сумматоры характеризуется разрядностью и бывают одно-, двух- и четырехразрядные. Рассмотрим принципы построения полных одноразрядных сумматоров, которые могут вычислять не только сумму S, но и разность D двух чисел А и В, т.е. будут работать либо как сумматор SM, или как вычитатель SUB (subtraktor). При этом, если на входе SM суммируются числа типа (1+1), то на выходе SM необходимо осуществить перенос Р полученной единицы в следующий (старший) разряд, а также перенос сигнала С, поступившего из предыдущего разряда. При вычитании (0-1) осуществляется заем Для расчета суммы S и разности D составим по таблице истинности, а логические выражения.
Аналогично для разности D запишем:
Следовательно, сумма S и разность D реализуются сумматором по модулю 2 на три входа либо используются две схемы И Для определения значений переносов Р и
Из карт Карно следует, что значения переносов
По выражениям (4.6) и (4.9) составим логическую схему двоичного одноразрядного сумматора SM.
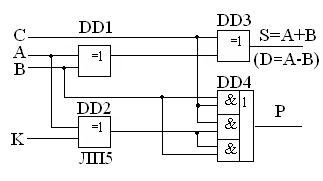
По выражениям (4.6) и (4.10) составим логическую схему одноразрядного универсального сумматора – вычитателя (SM-SUB).
Рисунок 4.8 – Схема сумматора-вычитателя
Согласно выражению (4.10) в схеме SM-SUB в режиме работы вычитающего устройства в качестве DD2 необходимо применить инвертор, но в данном варианте устройства используется сумматор по модулю два ЛП5, выполняющий роль схемы управления. При подаче на вход DD2 сигнала А и постоянного сигнала К=0 схема DD2 будет выполнять роль повторителя сигнала А и устройство SM-SUB на рисунке 4.8 будет осуществлять суммирование В многоразрядных сумматорах увеличение разрядности достигается путем каскадирования при этом выход переноса Р младшего разряда соединяют с входом переноса С старшего разряда. При работе SM в режиме суммирования на вход переноса младшего разряда подается лог. 0, а в режиме вычитания – лог. 1. Последовательный формирование бита переноса снижает быстродействие многоразрядных сумматоров. Для его повышения применяют параллельное формирование переносов в специальных блоках ускоренного переноса. Компаратор (comparator) предназначен для сравнения двух двоичных чисел. С помощью компаратора можно производить проверку равенства чисел или определить какое из них больше. На схемах компаратор обозначается буквами СМР либо (= =).
СМР подразделяется на одноразрядные и многоразрядные. Простейшим одноразрядным компаратором является схема Исключающее ИЛИ, с помощью которой реализуется функция неравнозначности ( На рисунке 4.9 показана реализация 4-разрядного компаратора, выполненного на схемах Исключающее ИЛИ (И
Рисунок 4.9 – Схема цифрового компаратора
При равенстве входных сигналов во всех разрядах выходной сигнал Составим таблицу истинности для одноразрядного универсального СМР, который кроме констатации равенства двух чисел может определить какое из них больше.
Таблица 4.8 – Таблица истинности универсального цифрового компаратора
Согласно таблицы 4.8 запишем логические функции, характеризующие признаки равенства или неравенства между входными числами А и В:
По полученным выражениям (4.11), (4.12) и (4.13) построим схему одноразрядного универсального компаратора (рисунок 4.9). При проектировании СМР за основу принята логическая схема И
Рисунок 4.9 – Схема универсального одноразрядного компаратора
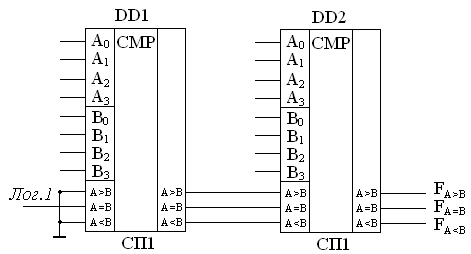
С целью повышения разрядности компараторы соединяют последовательно, как показано на рисунке 4.10 на примере двух 4-разрядных СМР.
Рисунок 4.10 – Вариант наращивания разрядности компараторов
Для нормального функционирования многоразрядного СМР входы младших разрядов DD1 необходимо подключать как показано на рис. 4.10. Сигналы на межразрядных входах и выходах будут словами кода "1 из 3", так как для нормальной работы СМР только на одном выходе должен присутствовать сигнал с активным уровнем. Преобразователи кодов (converter) предназначены для преобразования цифровой информации. На схемах преобразователи обозначаются буквами Рассмотрим синтез преобразователя двоично-десятичного кода в специальный семиразрядный код индикатора. Подсветка каждого сегмента цифрового индикатора, образующих цифры 0…9 (рисунок 4.11), производится подачей на них единичного сигнала, вызывая свечение сегментов в определенных комбинациях.
Рисунок 4.11 – Схема управления семисегментным индикатором
Из рис. 4.11 следует, что для цифры индикатора, например 6, которая задана двоично-десятичным кодом 0110, необходимо подсветить все сегменты, за исключением сегмента b. Выходные переменные а,…,g являются функциями аргументов A,…,D. Составим для функций
Таблица 4.9 – Таблица истинности преобразователя кодов
Согласно картам Карно запишем значения функций
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 896; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.19.115 (0.013 с.) |



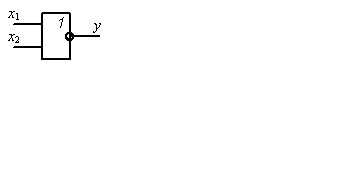



 …
…  поступают по информационным каналам n-разрядные сигналы. Число информационных каналов, коммутируемых на выход Q, составляет m = 2, 4, 8, 16. При m = 4 и Q = 1 мультиплексор имеет размерность 4 – 1. Это 4-канальный одноразрядный мультиплексор, на выход которого передается один из четырех входных сигналов.
поступают по информационным каналам n-разрядные сигналы. Число информационных каналов, коммутируемых на выход Q, составляет m = 2, 4, 8, 16. При m = 4 и Q = 1 мультиплексор имеет размерность 4 – 1. Это 4-канальный одноразрядный мультиплексор, на выход которого передается один из четырех входных сигналов. …
…  подается n-разрядный адресный код, при этом каждому информационному каналу присваивается свой адрес (номер), а общее число комбинаций адресных сигналов
подается n-разрядный адресный код, при этом каждому информационному каналу присваивается свой адрес (номер), а общее число комбинаций адресных сигналов  .
.
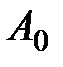
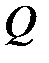
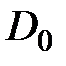



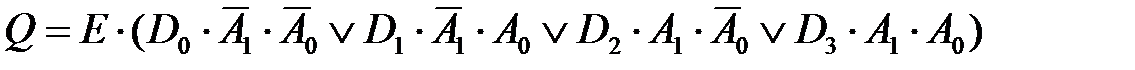 . (4.1)
. (4.1)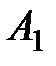 = 1, E = 1, то
= 1, E = 1, то  , следовательно, при E = 1 по адресному коду 10 на выход Q подключается сигнал, действующий на информационном входе
, следовательно, при E = 1 по адресному коду 10 на выход Q подключается сигнал, действующий на информационном входе  .
.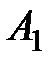

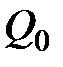
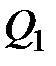


 (4.2)
(4.2)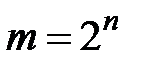 , а число выходов равно n (n – разрядность двоичного кода). На схемах шифраторы обозначаются буквами CD.
, а число выходов равно n (n – разрядность двоичного кода). На схемах шифраторы обозначаются буквами CD.
 (4.3)
(4.3)
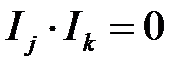 при j ¹ k.
при j ¹ k.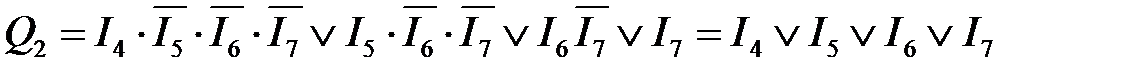 ;
;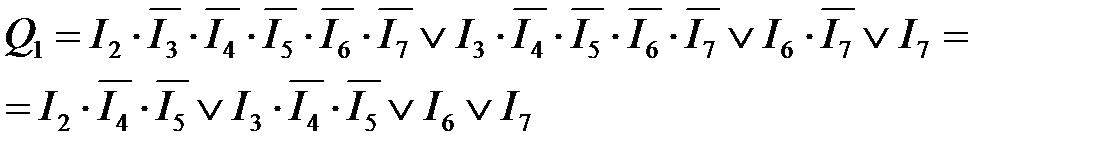 (4.4)
(4.4)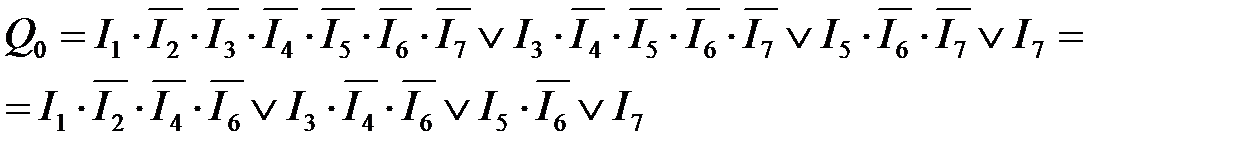
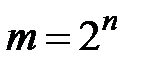 выходов. На схемах дешифраторы обозначаются буквами DC (рисунок 4.5).
выходов. На схемах дешифраторы обозначаются буквами DC (рисунок 4.5). ;
; ;
;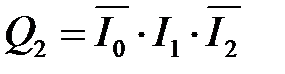 ;
; ; (4.5)
; (4.5)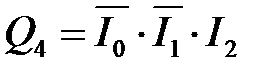 ;
;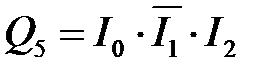 ;
;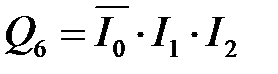 ;
; .
. . (4.6)
. (4.6)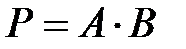 появляется на выходе только тогда, когда на входы А и В поданы единицы, реализуется логическим элементом И.
появляется на выходе только тогда, когда на входы А и В поданы единицы, реализуется логическим элементом И. единицы из предыдущего разряда и перенос
единицы из предыдущего разряда и перенос  в следующий разряд.
в следующий разряд. (4.7)
(4.7) (4.8)
(4.8) ЛИ.
ЛИ.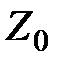 составим карты Карно согласно таблице истинности:
составим карты Карно согласно таблице истинности:
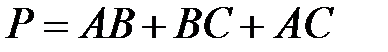

 и
и  равны:
равны: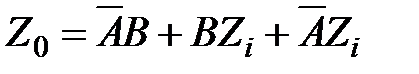 . (4.10)
. (4.10)
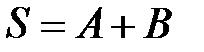 . При подаче на вход DD2 единицы (К=1) схема DD2 будет осуществлять инверсию сигнала А и устройство SM-SUB будет осуществлять вычитание чисел
. При подаче на вход DD2 единицы (К=1) схема DD2 будет осуществлять инверсию сигнала А и устройство SM-SUB будет осуществлять вычитание чисел  .
. ), и схема Исключающее ИЛИ-НЕ (И
), и схема Исключающее ИЛИ-НЕ (И  ЛИ-НЕ), с помощью которой реализуется функция равнозначности (
ЛИ-НЕ), с помощью которой реализуется функция равнозначности (  ). Эти функции представлены в табл. 3.5.
). Эти функции представлены в табл. 3.5.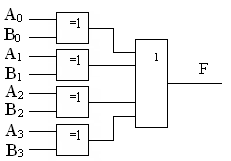
 , но если хотя бы в одном разряде сигналы различны, то выходной сигнал
, но если хотя бы в одном разряде сигналы различны, то выходной сигнал 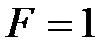 . Компаратор, приведенный на рисунке 4.9, осуществляет сравнение двух 4-разрядных чисел (кодов).
. Компаратор, приведенный на рисунке 4.9, осуществляет сравнение двух 4-разрядных чисел (кодов).

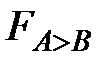
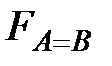

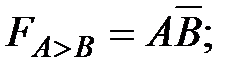 (4.11)
(4.11) (4.12)
(4.12) (4.13)
(4.13)
 .
.
 …
…  таблицу истинности (таблица 4.9), по которой отдельно для каждой функции составляем карты Карно, при этом "лишние" ячейки карт, где функции не определены, помечаем знаком * и доопределяем единицами.
таблицу истинности (таблица 4.9), по которой отдельно для каждой функции составляем карты Карно, при этом "лишние" ячейки карт, где функции не определены, помечаем знаком * и доопределяем единицами.

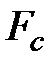

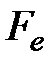
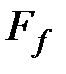





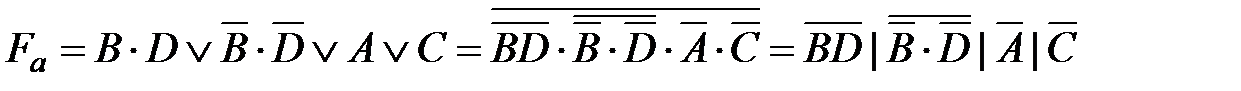 ;
;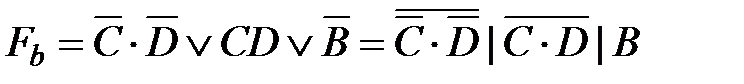 ;
; ;
;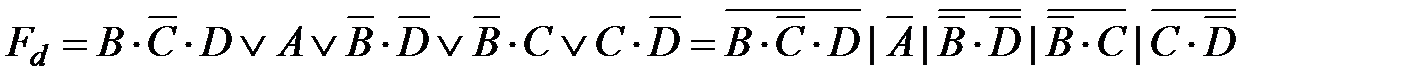 ;
; ;
;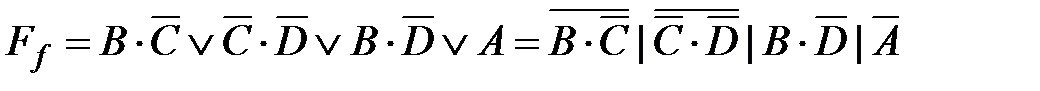 ;
;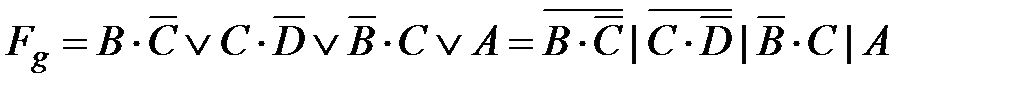 .
.


