
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 5. Типовые последовательностные схемыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В последовательностных схемах, в отличие от комбинационных, значения выходных сигналов зависят не только от значений входных сигналов, но и от последовательности их изменений. В последовательностных схемах (последовательных автоматах) зачастую необходимо введение в рассмотрение в явном виде времени для описания изменений сигналов. Аналитически это осуществляется путем использования операторов переходов d и Ñ. Потенциальные и импульсные сигналы. Сигнал называется потенциальным, если интервал времени Тi между соседними изменениями сигнала значительно больше времени установления переходных процессов в схеме, в которой он используется. Сигнал называется импульсным, если длительность его активного уровня того же порядка, что и время реакции схемы (схема должна отреагировать на воздействие импульсного сигнала, а он должен закончиться сразу же после окончания в схеме переходного процесса). При аналитическом описании схем, на которые воздействуют импульсные сигналы, используется понятие абстрактного импульсного сигнала, длительность которого бесконечно мала. Такие сигналы (dx,
Рисунок 5.1 – Разновидности импульсных сигналов
Оператор переходов d определяется соотношением
где dx – импульсный сигнал, принимающий единичное значение при изменении потенциального сигнала с 0 на 1; x(t) – значение потенциального сигнала в текущий момент времени; x(t – ∆t) – значение потенциального сигнала в предыдущий момент времени. Импульсный сигнал, соответствующий изменениям потенциального сигнала с 1 на 0:
Оператор переходов Ñ определяется соотношением
где Ñx = 1 как при изменении потенциального сигнала с 0 на 1, так и с 1 на 0. На рисунке 5.2 показана схема формирования импульсного сигнала dx и временные диаграммы ее работы в предположении, что используемые ЛЭ безынерционны.
Рисунок 5.2 – Схема формирования импульсного сигнала dx и временные диаграммы ее работы
Модель последовательного автомата. Эта модель состоит из комбинационной схемы (КС) и элементов задержки входных сигналов В общем случае автомат содержит m ЭП входных сигналов Qm,…Qr,…, Q1, имеет n физических входов, на которые подаются сигналы xn,...xp,… x1, и k физических выходов, с которых снимаются сигналы zk,...zq,… z1.
Рисунок 5.3 – Модель последовательного автомата
Совокупность входных сигналов автомата ν = (xn,..., x1) называется состояние входа автомата, совокупность выходных сигналов автомата l = (zk,..., z1) – состоянием выхода автомата, а совокупность выходных сигналов m = = (Qm,…, Q1) элементов памяти – внутренним состоянием автомата. При фиксированных значениях внутренних сигналов Qr автомат ведет себя подобно некоторой КС, т. е. реализует однозначное соответствие между значениями входных и выходных сигналов. Однако при изменении входных сигналов его реакция может выразиться в изменении внутренних сигналов. Если затем подать прежние значения входных сигналов, то соответствие между значениями входных и выходных сигналов может оказаться совсем другим. Последовательностная схема полностью описывается двумя функциями: функцией переходов автомата
показывающей зависимость состояния внутреннего сигнала Qr в последующий момент времени от состояния входа и внутреннего состояния автомата в текущий момент времени; и функцией выхода автомата
показывающей зависимость состояния выходного сигнала zq от состояния входа и внутреннего состояния автомата. Если для каждой упорядоченной пары внутренних состояний (mj, mk) имеется хотя бы одно состояние входа νi, которое переводит автомат из состояния mj в состояние mk, то говорят, что автомат обладает полной системой переходов. Данное условие должно выполняться как при j ¹ k, так и при j = k. Цифровые автоматы (последовательностные схемы) по способу воздействия на них входных информационных сигналов подразделяются на три основных класса: асинхронные потенциальные автоматы, синхронные автоматы и асинхронные импульсные автоматы. Каждый из классов автоматов можно разделить на несколько типов по другим признакам. На асинхронный потенциальный автомат воздействия производят непосредственно его входные информационные сигналы до тех пор, пока сохраняется их активный уровень. В синхронном автомате используется единый для всего автомата тактовый сигнал, который осуществляет на него импульсное воздействие в соответствии с уровнями входных информационных сигналов, т. е. в синхронном автомате последние только управляют воздействиями, а момент времени воздействия полностью определяется тактовым сигналом. Асинхронный импульсный автомат отличается от потенциального тем, что входные потенциальные сигналы производят на него импульсные воздействия в момент их изменения. Такие воздействия в синхронных автоматах производит только один сигнал – тактовый, а в асинхронных импульсных автоматах любой из входных сигналов может управлять воздействиями и производить их. Классы автоматов различаются только типом используемых в них ЭП: с потенциальным воздействием входных сигналов, импульсным воздействием только одного тактового сигнала или с импульсным воздействием нескольких входных сигналов (может быть и одного). Для проектирования цифровых автоматов используются не только ЛЭ, но и элементы памяти, в качестве которых чаще всего используются триггеры. Элементы памяти и триггеры являются элементарными автоматами, поэтому они, как и цифровые автоматы, делятся на те же три класса. Триггеры. Триггер – это цифровой автомат, имеющий не более двух устойчивых состояний для каждого допустимого состояния входа и обладающий полной системой переходов, внутренние состояния которого отождествляются со значениями выходного сигнала Q. Таким образом, состояние триггера полностью характеризуется значением его выходного сигнала Q. Так как любой автомат задается функциями переходов (5.4) и выхода (5.5), то из данного выше определения следует, что для триггеров r = 1, q = 1, z = Q. Ввиду этого закон функционирования триггеров полностью описывается одной только функцией переходов Q+ = F(xn,…, x1, Q) = F(ν, Q). Триггеры обычно имеют два выхода: прямой (основной) Q и инверсный RS-триггеры. Асинхронный потенциальный RS-триггер – это триггер с раздельной установкой состояний логического нуля и единицы (с раздельным запуском). Он имеет два информационных входа S и R. По входу S триггер устанавливается в состояние
Таблица 5.1 – Таблица переходов асинхронного RS-триггера
Функция переходов асинхронного RS-триггера может быть представлена в МДФ или МКФ, получаемым в результате минимизации по карте Карно:
Выражение (5.8) определяет условие реализации незапрещенных режимов работы RS-триггера. Синтезируем схему RS-триггера в соответствии с (5.6) на базе элементов ИЛИ-НЕ:
Рисунок 5.4 – Схема RS-триггера
D-триггером называется синхронный триггер с одним информационным входом, работающий так, что сигнал на выходе после переключения равен сигналу на входе D (delay – задержка) до переключения, т. е.
Таблица 5.2 – Таблица переходов синхронного тактируемого D-триггера
Функция переходов D-триггера описывается выражением
Рисунок 5.2 – Условное графическое обозначение D-триггера
Рисунок 5.3 – Временные диаграммы работы D-триггера T-триггер имеет информационный вход Т и динамический вход синхронизации (рисунок 5.4). При подаче на вход Т уровня логического 0, триггер находится в режиме хранения, при активации входа – в режиме инверсии: по каждому такту на входе C состояние выхода триггера меняется на противоположное (таблица 5.3).
Таблица 5.3 – Таблица переходов Т-триггера
Функция переходов Т-триггера описывается выражением
Рисунок 5.4 – Условное графическое обозначение Т-триггера JK-триггер имеет два информационных входа J и K и динамический вход синхронизации (рисунок 5.5). По входу J триггер устанавливается в состояние
Рисунок 5.5 – Условное графическое обозначение JK-триггера
Таблица переходов JK-триггера составляется на основе словесного описания условий получения требуемых режимов работы и представлена в таблице 5.4.
Таблица 5.4 – Таблица переходов синхронного JK-триггера
Функция переходов JK-триггера описывается выражением
Комбинированные триггеры отличаются наличием дополнительных входов – чаще всего асинхронных входов S и R для предварительной установки триггера в определенное состояние (логической 1 или 0). Синхронные двухступенчатые триггеры состоят из двух ступеней. Запись информации в первую ступень производится с появлением синхронизирующего импульса, а во вторую ступень – после окончания действия синхронизирующего импульса. Следовательно, двухступенчатые триггеры задерживают выходную информацию на время, равное длительности синхронизирующего импульса. Такие триггеры называют еще триггерами с внутренней задержкой. Регистр – устройство, предназначенное для кратковременного хранения и преобразования многоразрядных двоичных чисел. В качестве запоминающих элементов в регистрах используются триггеры. Вспомогательные элементы используются для осуществления следующих операций: - ввода и вывода из регистра хранимой информации; - преобразования кода числа, хранящегося в регистре; - сдвига числа влево или вправо на определенное число разрядов; - преобразования последовательного кода числа в параллельный и наоборот и другие. Вспомогательные элементы обычно строятся на основе комбинационных схем. Регистры классифицируют по различным признакам, основными из которых являются способ ввода информации в регистр и ее вывод и способ представления вводимой и выводимой информации. По способу ввода и вывода информации регистры подразделяются на: - параллельные (регистры памяти); - последовательные (регистры сдвига); - параллельно-последовательные. По способу представления вводимой и выводимой информации различают регистры однофазного и парафазного типа. В однофазных регистрах информация вводится либо в прямом, либо в обратном коде, а в парафазных – одновременно в прямом и обратном кодах. Вывод информации из регистров может осуществляться как в прямом, так и в обратном коде. Различают одно- и многоканальные регистры в зависимости от числа источников информации, с которых она поступает на входы регистра. В простейшем регистре триггеры соединены последовательно, т. е. выходы предыдущего триггера передают информацию на входы последующего. Тактовые входы C триггеров соединены параллельно. Такой регистр имеет один вход и один выход – последовательные. Вход управления – тактовый вход C. Если ко входу каждого триггера добавить разрешающую логику, то можно осуществить параллельную загрузку данных в регистр. Можно предусмотреть логическую схему параллельного отображения выходных данных. Как правило, выходные элементы такой схемы имеют z-состояния, позволяющие поочередно выдавать информацию по многопроводной шине данных. Регистры могут быть двунаправленные, т. е. записанную информацию можно сдвигать по линейке триггеров вправо или влево. Для включения режима сдвига предусматривают специальный вход. Существуют многорежимные регистры, у которых входные и выходные линии данных объединены в одну линию (порт данных). Эта линия по соответствующей команде (т. е. имеет дополнительный вход) может быть и входной, и выходной. Существуют специализированные регистровые микросхемы для построения АЦП. Счетчиком называют устройство, предназначенное для подсчета числа импульсов, поданных на вход и фиксации этого числа в каком-либо коде. Простейший многоразрядный двоичный делитель частоты с коэффициентом деления Основными характеристиками счетчика являются коэффициент счета и быстродействие. Коэффициент счета Kсч характеризует число устойчивых состояний счетчика, т.е. предельное число импульсов, которое может быть сосчитано счетчиком. Быстродействие счетчика определяется двумя параметрами: разрешающей способностью tразр.сч ивременем установки кода счетчика tуст. Под разрешающей способностью подразумевается минимальное время между двумя входными импульсами, в течение которого еще не возникают сбои в работе счетчика. Обратная величина Время установки кода tуст равно времени между моментом поступления входного импульса и переходом счетчика в новое устойчивое состояние. Временные свойства зависят от временных характеристик триггеров и способа ихсоединения между собой. Цифровые счетчики классифицируются следующим образом: - по коэффициенту счета: двоичные, двоично-десятичные или с другим модулем счета; - по направлению счета: однонаправленные (суммирующие – с увеличением счёта, вычитающие – с уменьшением счёта), двунаправленные или реверсивные; - по способу организации внутренних связей: с непосредственными связями, со связями по цепям переноса (счетчики с переносом) и с комбинированными связями; - по способу подачи счетных импульсов: параллельные, последовательные и параллельно-последовательные. Классификационные признаки независимы и могут встречаться в разных сочетаниях. Параллельный счетчик с непосредственными связями характеризуется одновременным поступлением счетного импульса на счетные входы всех разрядов счетчика и непосредственным подключением выходов младших разрядов к управляющим входам старших разрядов счетчика. Срабатывание триггеров параллельного счетчика происходит синхронно, и задержка переключения всего счетчика равна задержке для одного триггера. Такие счетчики обладают наибольшим быстродействием. Недостаток параллельных счетчиков на многовходовых триггерах состоит в том, что необходимо иметь различное число входов в каждом из разрядов. Поэтому при большом числе разрядов счетчик разбивается на группы, например, по четыре разряда. Последовательные счетчики с непосредственными связями. В таких счетчиках управляющими сигналами для старших разрядов являются уровни сигналов с информационных выходов младших разрядов. Максимальная величина времени установки счетчика tуст в счетчиках последовательного типа определяется суммарной задержкой передачи информации из младшего разряда в старший. где N – число разрядов счетчика, а tt – задержка переключения триггера. Последовательные счетчики являются простейшими по схемотехнической реализации, но они обладают наименьшим быстродействием. Реверсивные счетчики в зависимости от сигналов управления осуществляют суммирование импульсов или вычитание. Методику синтеза синхронного счетчика на базе заданного типа триггеров, реализующий определенный граф переходов, рассмотрим на примере. Пусть задан граф переходов:
Рисунок 5.6 – Функциональная схема счетчика
В соответствии с графом переходов составляется таблица переходов счетчика и определяются значения функций возбуждения каждого из триггеров. Так как общее количество состояний трехразрядного счетчика – 8, а определены только 6, то необходимо доопределить переходы, т.е. указать в какое состояние из разрешенных графом должен перейти счетчик, если перед этим он каким – либо образом (например, при включении устройства или в результате воздействия помехи) установился в запрещенное графом состояние. Запрещенные состояния проектируемого счетчика 0 и 4. Потребуем, чтобы из этих состояний он переходил в состояние 1. Таблица переключений проектируемого счетчика будет выглядеть следующим образом (таблица 5.5).
Таблица 5.5 – Таблица переключений проектируемого счетчика
В таблице использованы следующие обозначения: Q – состояние выхода триггера, предшествующее тактовому импульсу; Затем осуществляется минимизация функций возбуждения J 0 = F0(Q 0, Q 1, Q 2), K 0 = F1(Q 0, Q 1, Q 2), D 1 = F2(Q 0, Q 1, Q 2), Т 2 = F2(Q 0, Q 1, Q 2) любым известным методом и синтезируются комбинационные схемы реализующие эти функции. Для примера синтезируем схемы СВ1 и СВ2, формирующие сигналы возбуждения J 0 и K 0, соответственно.
J 0 = 1. Таким образом СВ1 представляет собой генератор логической “единицы”.
Следовательно, для возбуждения входа K триггера D1 необходимо использовать сигнал
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 896; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.141.69 (0.014 с.) |

 и Ñx) показаны на рисунке 5.1 и соответствуют изменениям потенциального сигнала x с 0 на 1 и (или) с 1 на 0. Реальные импульсные сигналы всегда имеют конечную длительность, которая определяется временем реакции схемы. В зависимости от быстродействия ЛЭ, из которых построена схема, время реакции может изменяться в широких пределах. Понятие абстрактного импульсного сигнала позволяет абстрагироваться от физических параметров конкретных схем.
и Ñx) показаны на рисунке 5.1 и соответствуют изменениям потенциального сигнала x с 0 на 1 и (или) с 1 на 0. Реальные импульсные сигналы всегда имеют конечную длительность, которая определяется временем реакции схемы. В зависимости от быстродействия ЛЭ, из которых построена схема, время реакции может изменяться в широких пределах. Понятие абстрактного импульсного сигнала позволяет абстрагироваться от физических параметров конкретных схем. , (5.1)
, (5.1) , (5.2)
, (5.2)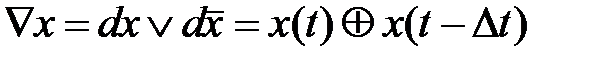 , (5.3)
, (5.3) на время ∆t, включенных в цепях обратных связей (рисунок 5.3). Элементы задержки производят запоминание внутренних сигналов КС, т. е. они являются элементами памяти (ЭП). Эти сигналы появляются на входах КС через время ∆t и могут вызвать изменение ее выходных сигналов. Понятно, что если сигнал
на время ∆t, включенных в цепях обратных связей (рисунок 5.3). Элементы задержки производят запоминание внутренних сигналов КС, т. е. они являются элементами памяти (ЭП). Эти сигналы появляются на входах КС через время ∆t и могут вызвать изменение ее выходных сигналов. Понятно, что если сигнал  , то сигнал
, то сигнал  =
=  (t + ∆t).
(t + ∆t). , (5.4)
, (5.4) , (5.5)
, (5.5) . Состояние триггера определяется значением потенциала на прямом выходе. Если, например, на прямом выходе имеется потенциал, соответствующий логической 1, то триггер находится в единичном состоянии (при этом потенциал на инверсном выходе соответствует логическому 0). В противном случае триггер находится в нулевом состоянии. Число входов схемы управления зависит от структуры и функций, выполняемых триггером. В настоящее время существует несколько разновидностей триггерных схем, различающихся по функциональным возможностям: RS-, D-, JK- и T-триггеры.
. Состояние триггера определяется значением потенциала на прямом выходе. Если, например, на прямом выходе имеется потенциал, соответствующий логической 1, то триггер находится в единичном состоянии (при этом потенциал на инверсном выходе соответствует логическому 0). В противном случае триггер находится в нулевом состоянии. Число входов схемы управления зависит от структуры и функций, выполняемых триггером. В настоящее время существует несколько разновидностей триггерных схем, различающихся по функциональным возможностям: RS-, D-, JK- и T-триггеры. , а по входу R – в состояние
, а по входу R – в состояние  .
. (5.6)
(5.6) (5.8)
(5.8)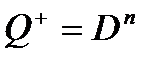 . Основное назначение D-триггеров – задержка сигнала, поданного на вход D. Он имеет информационный вход D (вход данных) и вход синхронизации C. Вход синхронизации C может быть статическим (потенциальным) и динамическим. У триггеров со статическим входом C информация записывается в течение времени, при котором уровень сигнала
. Основное назначение D-триггеров – задержка сигнала, поданного на вход D. Он имеет информационный вход D (вход данных) и вход синхронизации C. Вход синхронизации C может быть статическим (потенциальным) и динамическим. У триггеров со статическим входом C информация записывается в течение времени, при котором уровень сигнала  . В триггерах с динамическим входом C информация записывается только в течение перепада напряжения на входе C. Таблица переходов D-триггера представлена в таблице 5.2, его условное обозначение и временные диаграммы работы на рисунках 5.2 и 5.3.
. В триггерах с динамическим входом C информация записывается только в течение перепада напряжения на входе C. Таблица переходов D-триггера представлена в таблице 5.2, его условное обозначение и временные диаграммы работы на рисунках 5.2 и 5.3.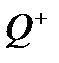

 (5.8)
(5.8)
 (5.9)
(5.9) , а по входу K – в состояние
, а по входу K – в состояние 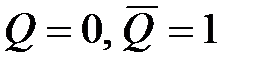 . Он отличается от RS-триггера прежде всего тем, что в нем устранена неопределенность, которая возникает в RS-триггере при определенной комбинации входных сигналов.
. Он отличается от RS-триггера прежде всего тем, что в нем устранена неопределенность, которая возникает в RS-триггере при определенной комбинации входных сигналов.
 (5.10)
(5.10) можно получить, соединив последовательно n триггеров T-типа. Более общее название для делителей частоты – счетчики. Основой любого счетчика является линейка из нескольких триггеров.
можно получить, соединив последовательно n триггеров T-типа. Более общее название для делителей частоты – счетчики. Основой любого счетчика является линейка из нескольких триггеров. называется максимальной частотой счета.
называется максимальной частотой счета. ,
,
 . Он характеризует последовательность изменения состояния триггеров синтезируемого счетчика. Для реализации требуемого счетчика потребуется три синхронных триггера (двоичный код, соответствующий наибольшему выходному состоянию, является трехразрядным: 710 = 1112, кроме того, общее количество состояний счетчика в цикле счета, равное 6, также описывается как минимум трехразрядным двоичным кодом). Для примера первый сегмент счетчика реализуем на базе JK-триггера, второй – на базе D-триггера, третий – на базе Т-триггера. Так как требуется синтезировать синхронный счетчик, то тактовые импульсы (сигнал С) подаются на триггеры параллельно. Функциональная схема счетчика представлена на рисунке 5.6. Схемы возбуждения (СВ1…СВ4) должны формировать сигналы возбуждения триггеров счетчика, обеспечивая требуемую по заданию последовательность его переключения. Таким образом дальнейший синтез счетчика сводится к синтезу схем возбуждения.
. Он характеризует последовательность изменения состояния триггеров синтезируемого счетчика. Для реализации требуемого счетчика потребуется три синхронных триггера (двоичный код, соответствующий наибольшему выходному состоянию, является трехразрядным: 710 = 1112, кроме того, общее количество состояний счетчика в цикле счета, равное 6, также описывается как минимум трехразрядным двоичным кодом). Для примера первый сегмент счетчика реализуем на базе JK-триггера, второй – на базе D-триггера, третий – на базе Т-триггера. Так как требуется синтезировать синхронный счетчик, то тактовые импульсы (сигнал С) подаются на триггеры параллельно. Функциональная схема счетчика представлена на рисунке 5.6. Схемы возбуждения (СВ1…СВ4) должны формировать сигналы возбуждения триггеров счетчика, обеспечивая требуемую по заданию последовательность его переключения. Таким образом дальнейший синтез счетчика сводится к синтезу схем возбуждения. 2
2
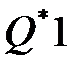


 .
. с инверсного выхода триггера D2.
с инверсного выхода триггера D2.


