
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перевод чисел из одной системы счисления в другую.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для любого числа Е в системе счисления с основанием q можно определить его эквивалентное десятичное значение (значение в системе с основанием 10) по выражениям (1.1)…(1.3). При вычислении суммы полагаем, что все значения ер и qp представлены в десятичной системе счисления. Для приведенных выше примеров записи двоичных, восьмеричных и шестнадцатеричных чисел:
Для преобразования десятичного числа в числа других систем счисления возможны два подхода. Первый из них является обратным процессу, описанному выше. Десятичное число представляется взвешенной суммой степеней основания системы, в которую преобразуется десятичное число, и полученные веса используются для записи числа. Такой подход прост при преобразовании в двоичную систему, когда число разлагается по степеням 2 с весовыми коэффициентами 0 и 1:
Другой метод справедлив для преобразования целых чисел (или целых частей нецелых чисел) и базируется на выражении (1.2) и использует последовательное целочисленное деление десятичного числа на основание системы, в которую оно преобразуется, и записи остатка после каждого такого деления как результата преобразования, пока частное в целых числах не будет равно 0, причем первый остаток деления пишется на месте МЗР, а последний остаток – на месте СЗР:
При записи числа в шестнадцатеричной системе по данному алгоритму необходимо осуществлять замену двузначного десятичного остатка (10…15) деления на соответствующий символ (A…F). Для преобразования дробных частей нецелых чисел используется последовательное не деление, а умножение на основание системы счисления, и записи целой части после каждого такого умножения как результата преобразования до тех пор пока не будет достигнута целая 1 или до достижения требуемой точности (не всякая дробная часть десятичного числа может быть точно представлена в двоичном коде):
Преобразования восьмеричного (шестнадцатеричного) числа в двоичную форму и наоборот можно осуществлять через десятичную систему по описанным выше процедурам. Однако в силу того, что основаниями этих систем являются степени 2 (21, 23, 24), преобразование можно осуществить непосредственно путем замены символа каждого разряда восьмеричного (шестнадцатеричного) числа тремя (четырьмя) двоичными битами и их последовательной записью без изменения порядка:
75308 = 111 101 011 0002 3F516 = 0011 1111 01012 78 = 710 = 1112 316 = 310 = 00112 58 = 510 = 1012 F16 = 1510 = 11112 38 = 310 = 0112 516 = 510 = 01012 08 = 010 = 0002
Для перевода двоичного числа в восьмеричную (шестнадцатеричную) систему поступают наоборот: двоичное число, начиная с МЗР, разбивается на триады (тетрады) по три (четыре) разряда (при необходимости слева двоичное число дополняется нулями), а затем каждая триада (тетрада) заменяется соответствующим восьмеричным (шестнадцатеричным) символом без изменения порядка записи. Представление чисел со знаком. Большинство цифровых устройств позволяют работать как с положительными, так и отрицательными числами, поэтому в них требуется какой либо способ представления знака числа (“+” или “–“). Обычно с этой целью к двоичному числу добавляют еще один бит, который называется знаковым (его нельзя учитывать как значащий). В общем случае если знаковый бит содержит 0, то число считается положительным, если 1 – то отрицательным (выделен полужирным): 0 1101002 = + 5210 1 1101002 = – 5210 Крайний левый бит – знаковый, а шесть оставшихся представляют модуль числа. Биты модуля – действительный двоичный эквивалент десятичного значения числа, а знаковый используется, чтобы показать принадлежность данного числа к положительным или отрицательным числам. Такая система представления чисел называется системой типа знак-модуль и служит для представления двоичных чисел со знаком. Эта система относится к прямым методам представления чисел, однако в цифровых устройствах она обычно не используется в силу сложности реализации вычислительных процессов. Наиболее распространенная система представления чисел со знаком – дополнительный код. Обратный и дополнительный код. Обратный код (первое дополнение) двоичного числа получают заменой в записи числа каждого 0 на 1 и каждой 1 на 0. Иначе говоря, значение каждого бита числа изменяется на противоположное (обратное): 10101100 (прямой код) → 01010011 (обратный код). Сложение прямого кода числа с его же обратным кодом дает в результате 1 во всех значащих битах, т.е. Апр + Аобр = 2N – 1, где N – разрядность двоичного представления числа А. Дополнительный код двоичного числа получают из обратного кода путем сложения его с 1: 01010011 (обратный код) + 1 = 01010100 (дополнительный код). Дополнительный код применяется для представления чисел со знаком следующим образом: 1. Если число положительное, то его модуль представляется в прямом двоичном коде, а знаковый бит ставится перед старшим значащим битом и содержит 0. 2. Если число отрицательное, то его модуль представляется в дополнительном коде, а знаковый бит ставится перед старшим значащим битом и содержит 1. Использование дополнительного кода позволяет осуществить операцию вычитания двоичных чисел через операцию сложения, тем самым сократить аппаратные затраты при выполнении вычислений в цифровых устройствах. Наряду с двоичным прямым или дополнительным кодом для представления числовой информации применяют и другие виды кодов. Достаточное распространение в цифровых устройствах получили двоично-десятичный код, код Грея, унитарный код. Двоично-десятичный код. Для представления и обработки в цифровых устройствах десятичных чисел также необходимо использовать их двоичное кодирование. С этой целью наиболее часто применяется код прямого замещения, называемый иначе двоично-десятичным кодом 8-4-2-1, при получении кодового слова которого каждая цифра 0, 1,..., 9 десятичного числа заменяется прямым двоичным эквивалентом 0000, 0001,..., 1001 – двоичной тетрадой (шесть двоичных тетрад 1010, 1011, 1100, 1101, 1110 и 1111 при таком кодировании не используются). Так, можно записать, что 201110 = (0010 0000 0001 0001)2-10. Код Грея. Отличительная особенность этого кода в том, что два соседних кодовых слова отличаются только в одном разряде. Существует два удобных способа строить код Грея с любым числом битов. Первый метод основан на рекурсивном использовании следующих правил: 1. В однобитном коде Грея два кодовых слова: 0 и 1. 2. Первые 2 n кодовых слов (n +1)-разрядного кода Грея равны кодовым словам n-разрядного кода Грея, записанным по порядку и дополненным 0 в старшем разряде. 3. Последние 2 n кодовых слов (n +1)-разрядного кода Грея равны кодовым словам n-разрядного кода Грея, но записанным в обратном порядке и дополненным 1 в старшем разряде. Второй метод позволяет получать n -разрядное кодовое слово кода Грея непосредственно из соответствующего кодового слова n-разрядного двоичного кода: 1. Биты в n -разрядных кодовых словах двоичного кода и кода Грея нумеруются справа налево от 0 до n – 1. 2. i-й бит в кодовом слове кода Грея равен 0, если i-й и (i +1)-й биты в соответствующем слове двоичного кода одинаковые, в противном случае i-й бит равен 1 (если i +1 = n, то n -й бит в слове двоичного кода принимается равным 0). Унитарный код (код “1 из N”). Отличительной особенностью кода является то, что в N-разрядном кодовом слове символ “1” присутствует только в одном разряде. Например, кодовые слова 4-х разрядного унитарного кода выглядят следующим образом: 0001, 0010, 0100, 1000. Остальные кодовые группы считаются запрещенными. Алфавитно-цифровые коды. Кроме числовых данных цифровые устройства в ряде случаев должны обрабатывать знако-буквенную информацию. Для представления этой информации в двоичном виде используют разнообразные алфавитно-цифровые коды. Типичным представителем такой группы кодов является код ASCII (American Standard Code for Information Interchange – Американский стандартный код для обмена информацией). Его кодовая таблица с расширением для кириллицы представлена на рисунке 1.1. Из таблицы видно, что латинская буква “А” кодируется как 4116, “b” – 6216, а буква “И” – 8816.
Рисунок 1.1 – Кодовая таблица ASCII
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1423; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.184.125 (0.007 с.) |

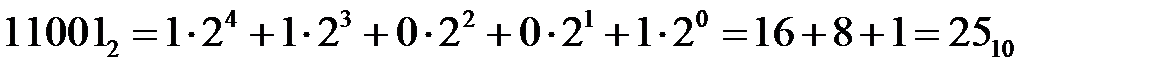 ,
,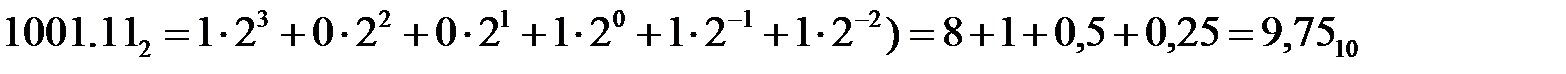 .
.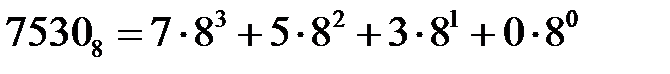 = 3584 + 320 + 24 = 392810,
= 3584 + 320 + 24 = 392810,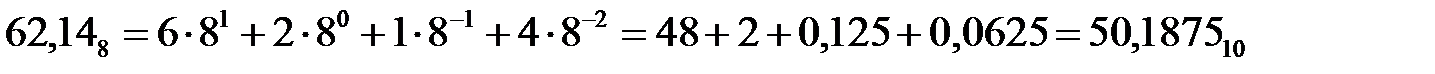 ,
,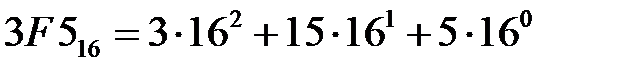 = 768 + 240 + 5 = 101310,
= 768 + 240 + 5 = 101310,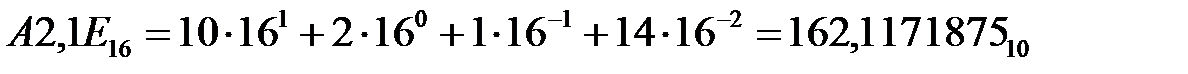 .
.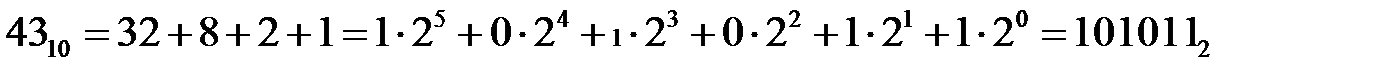 .
.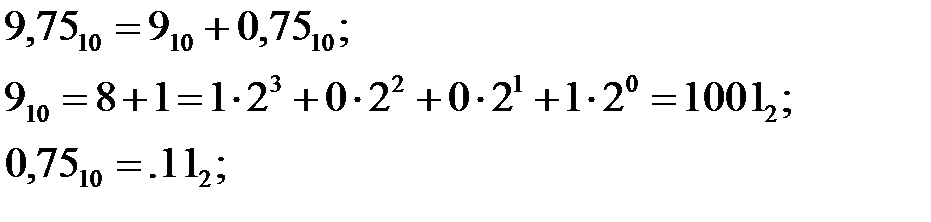 .
.


